Az akkord - stadopedia módszere
Ebben a módszerben a nemlineáris függvény f (x) egy külön résen
[a, b] helyébe egy a (a, f (a)) és (b, f (b)) pontokon áthaladó akkord lép,
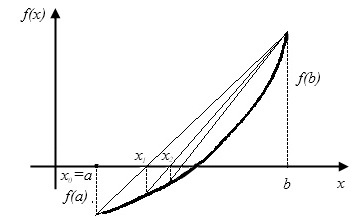
Fig.2.4. Az akkordok módszere. A b rés jobb vége álló helyzetben van
Az akkord egyenlete :. Találjuk meg az akord metszéspontját a vízszintes tengellyel. Feltételezve és. kapunk
Az x1 pont a szegmens új határa, ahol a gyökér van. Ezzel pont koordinátáit (x1, f (x1)) és a megfelelő előző intervallum határa (b, f (b)) ismét végre akkord találni stb egy x1, x2, x3, ... xn, ... szekvenciát kapunk, amely az egyenlet gyökeréhez konvergál.
A második származék megtartja a folyamatos jelzést. Következésképpen két eset lehetséges. Ha f (b) # 903; f "(b)> 0. akkor az akkordnak van egy jobb végpontja, és az x0, x1, ... xn sorozata megközelíti a bal oldali gyökeret. Az x0 kezdeti közelítéshez természetesen
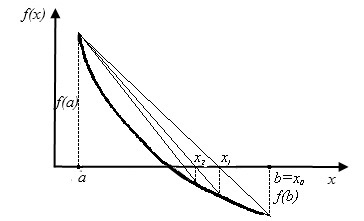
Ábra 2.5. Az akkordok módszere. Az a hézag bal vége álló helyzetben van
Ha f (a) # 903; f "(a)> 0. akkor az akkordnak van egy bal oldali vége, és az x0, x1, ... xn ... szekvencia megközelíti a gyökeret a jobb oldalon. Az x0 kezdeti közelítéshez vegye a b
A pontosság becsléséhez képletet használhatunk
ahol a gyökér gyökér, a hozzávetőleges gyökér. az [a, b] intervallumon. Addig számolunk, amíg a feltétel teljesül. Ha van egyenlőtlenség. akkor a számla megszüntethető.
2.4. Példa. Keressük meg az egyenlet gyökereit az x 4 -x-1 = 0 akkord módszerrel
A megoldást a Mathcad csomag segítségével találjuk meg.
A függvény monotone az intervallumokban (-∞, 0.63), (0.63, ∞), és a jeleket az intervallumok végein változtatja. Az egyenletnek két gyökere van. A gyökerek szétválasztásának szüneteit a minták módszerével szűkítjük, azaz helyettesítés.