Abszolút és robusztus stabilitás
1. Az abszolút stabilitás fogalma
2. Popov abszolút stabilitásának kritériumai
3. Az instabil lineáris rész abszolút stabilitásának vizsgálata
4. A Voronov körkörös teszt
5. Robusztus stabilitás
1. Az abszolút stabilitás fogalma
Az abszolút stabilitási módszert alkalmazzuk a nemlineáris rendszerek stabilitásának vizsgálatára, amikor a nemlineáris elemek jellemzői pontatlanul ismertek. Az információ teljességének oka lehet a gyártási hiba, bizonyos tényezők figyelmen kívül hagyása, elemek öregedése stb. A rendszer stabilitásának biztosítása érdekében, a nem lineáris hiányosságok ellenére, az abszolút stabilitás fogalmát vezették be. Ugyanebből a célból a nonlinearitások osztályai kerülnek bevezetésre [4]. Például az 1. ábrán látható az osztály nemlinearitása. Definíció szerint minden nemlineáris függvény tartozik ehhez az osztályhoz, amelynek gráfja az egyenes vonalak és a. hol.
Leggyakrabban a következő típusú nemlineáris elemek használatosak: [0; k], (1. ábra, b); osztály (2. ábra, a); osztály [k 1; k 2] ahol. (2. ábra, b). A bonyolultabb kifejezések által definiált nemlinearitások egyéb osztályai [2, 4].
A gyakorlatban a nem-linearitás osztályát úgy kell megválasztani, hogy az öregedés folyamatában, a rendszer elemeinek romlása vagy bármely más természetes változás esetén a nemlinearitás megőrzi az eredeti osztályhoz való tartozását.
Definíció. A rendszert teljesen állandónak nevezik. ha egyedi egyensúlyi pozíciója általánosan aszimptotikusan stabil egy adott osztály bármely nem-linearitása esetén.
2. Popov abszolút stabilitásának kritériumai
Az abszolút stabilitás vizsgálatához számos feltételt javasoltak az abszolút stabilitás szempontjából. Ezek közül a legszélesebb körben a következő volt: a VM Popov stabilitási kritérium és az AA Voronov által javasolt körkörös kritérium.
A Popov-kritérium a [0, k] osztályú nemlinearitású rendszerek abszolút stabilitásának vizsgálatára szolgál. Ezt a kritériumot alkalmazva a rendszer szerkezeti diagramja a 2. ábrán látható formára redukálódik. 3.
ahol # 150; vezetés # 150; állami vektor.
A (1) és a (3) -hoz Laplace képekhez jutunk
A Popov-kritérium csak akkor alkalmazható, ha az alábbi feltételek teljesülnek:
c) Egy lineáris rendszer, amelyet nemlineáris formában kaptunk, amikor helyettesítettük. aszimptotikusan stabil, vagyis kielégíti a Hurwitz vagy Nyquist kritériumot minden [0; k].
Popov kritériuma. A 3. ábrán látható nemlineáris rendszer abszolút stabil, ha a fenti feltételek a) # 150; c), és minden [0,] esetében a következő egyenlőtlenség áll:
itt # 150; tetszőleges szám. ■
Popov kritérium elegendő.
A Popov-teszt geometriai formája. A rendszer grafikai vizsgálatához a Popov-hodográf abszolút stabilitásra épül. amelyet az alábbi képlet határoz meg:
Itt () és () # 150; valódi és képzeletbeli részek. azaz = () + (). Emlékezzünk arra, hogy a Nyquist-hodographot a 3. ábrán látható rendszer lineáris részére építjük fel. A 4. ábra Popov és Nyquist hodográfjait mutatja be. ugyanarra a rendszerre.
Popov tesztjének grafikus változata a következő: Ha egy ponton keresztül egyenes vonalat rajzolhatunk úgy, hogy a Popov időgráfja teljesen jobbra van elhelyezve, akkor a rendszer teljesen stabil. ■
Az 1. ábrán. Az 5. ábra a teljesen stabil rendszerhez (5a. Ábra) épített Popov-hódográfokat mutatja, valamint egy olyan rendszert, amely nem teljesen stabil (5b.
A pilóta tanulmányozásával Popov [25. 185], hogy ha a rendszer lineáris része inerciális összeköttetések egymás utáni kombinációja, és nem több, mint egy integráló kapcsolat, akkor a megfelelő Popov-hodográf konvex lesz (5. ábra, b). Ebben az esetben a korlátozó érték, amelyre a rendszer teljesen stabil a Popov-teszt szerint, egybeesik az értékével. amelyet a Nyquist stabilitási kritérium határoz meg, ha a nemlinearitást egyenes vonal váltja fel. Ezért, ha a nemlineáris rendszer lineáris része a megjelölt formával rendelkezik, akkor az abszolút stabilitás vizsgálatához a Popov-teszt helyett a Nyquist-kritériumot alkalmazhatjuk.
1. példa Vizsgáljuk meg a rendszer abszolút stabilitását, amelynek sémáját a 2. ábrán mutatjuk be. 6.
A nem linearitás a szektorhoz tartozik [0; 10], azaz. [0; 10].
A megoldás. A probléma megoldásához megépítjük a Popov-hodográfot. Ehhez először választani kell a valódi és a képzeletbeli részeket. Van
A frekvenciaértékek megadása. össze fogjuk fordítani az 1. táblázatot.
A megfelelő Popov hodográfja a 3. ábrán látható. 7. Látható, hogy ebben az esetben egyenes vonalat rajzolhat (150, 0,1, j 0), hogy a Popov időgörbéje jobbra legyen elhelyezve. Következésképpen a vizsgált rendszer teljesen stabil. ■
2. példa Abszolút stabilitás vizsgálata olyan rendszer, amelynek szerkezeti diagramját a 2. ábrán mutatjuk be. 3, és a lineáris rész átviteli függvénye
Nem linearitás [0; 5], azaz. k = 5.
A megoldás. Mivel a lineáris rész inerciális kapcsolatok egymást követő kombinációja, a Nyquist-kritérium használható a probléma megoldására. Az 1. ábrán. A 8. ábra a Nyquist görbék helyének általános áttekintését mutatja egy adott formájú átviteli függvényt használó rendszerek esetén.
Nyilvánvaló, hogy ebben az esetben a probléma megoldása elegendő ahhoz, hogy összehasonlítsuk az értékeket a k = 5 értékkel. Ezért írjuk le és keressük meg a frekvenciát. Van
Ha a nevező képzeletbeli részét ez a kifejezés nullázza, akkor kapjuk
Itt van. Aztán. Állapot (5), az 1. ábrával összhangban. 8, elégedett, ha. azaz if. Következésképpen a vizsgált rendszer teljesen stabil. ■
Nem nehéz látni, hogy ha a lineáris része a nemlineáris rendszer egy szekvenciát? -Inflammatory vegyületet tehetetlenségi linkek és egy integrátor, a tanulmány teljes stabilitást nagymértékben egyszerűsödik, mert ahelyett, Popov ismérvet lehet alkalmazni a Nyquist kritériumot.
3. Az instabil lineáris rész abszolút stabilitásának vizsgálata
Az abszolút stabilitással kapcsolatos minden ismert kritériumot abban az esetben formulálják, amikor a rendszer lineáris része aszimptotikusan stabil. Ezért az instabil lineáris résznél az abszolút stabilitási kritériumok alkalmazhatóságának biztosítása érdekében először át kell alakítani a rendszert úgy, hogy a transzformált rendszer lineáris része stabil legyen. E célból általában további visszajelzést alkalmaznak.
Vegyük például figyelembe a 6. ábrán látható rendszert. 9, a [25], ahol az átviteli függvény
és a nemlinearitás a [0,2; 6], azaz.
Keresse meg azokat a feltételeket, amelyek mellett az adott rendszer teljesen stabil.
Ebben az esetben a lineáris elem instabil, ezért további korlátozásokat vezetünk be az átviteli együtthatóval. amint az az 1. ábrán látható. 9, a. Mivel a gépelt kapcsolatok kompenzálják egymást, az eredményül kapott rendszer egyenértékű az eredeti változattal. Ezután a pozitív visszacsatoló bemenetet a rendszer kimenetéről az összehasonlító elem kimenetére továbbítjuk, amint az az 1. ábrán látható. 9, b. Az összehasonlító elemen keresztül történő átvitel miatt ez a kapcsolat negatívvá válik, de az így létrejövő rendszer az előzőhöz hasonlóan az eredetihez hasonló lesz.
Az átviteli függvény (6) és a megfelelő áramkör nemlinearitása (9. ábra, c) a képletek
Nyilvánvalóan a vizsgált esetben
Mivel a c () (7) rendszernek stabilnak kell lennie, a vizsgált rendszer teljesen stabil lehet, ha csak.
Figyelembe véve Popov kritériumának alkalmazását, elfogadjuk. Aztán. és a feltétel magában foglalja az egyenlőtlenséget vagy.
A vizsgált esetben a lineáris rész sorrendje két, így amikor és a Popov utazási ideje a negyedik és a harmadik negyedben helyezkedik el, ahogy az az 1. ábrán látható. 7. Továbbá a popov-vonalat (# 150; 1 / 5,8; j 0) át lehet végezni, hogy a Popov-kritérium teljesüljön.
Így a vizsgált rendszer abszolút stabil lesz u.
4. A Voronov körkörös teszt
A Voronov-kritérium lehetővé teszi az abszolút stabilitás vizsgálatát, ha a nemlinearitás megfelel a feltételeknek:
Definíció. Ha () [k 1; k 2] és állapotát
hol. akkor a lineáris rendszer teljesen stabil. ■
Grafikusan, a feltétel (8) Voronova kritérium az, hogy az abszolút stabilitás a nemlineáris rendszer elég ahhoz, hogy Nyquist poláros telek a lineáris része a rendszernek (ábra. 3) nem „jel” a korlátozott területen, ábrán látható. Ábra és 10. 11 # 150; 13. Az 1. ábrán. 10 ez a kör egy kör és a keltetés mutatja.
Az 1. ábrán. 10 # 150; A "tiltott területek" mind a nem lineáris (a), mind a Nyquist-idõt a (b) rendszer lineáris részéhez árnyékolják.
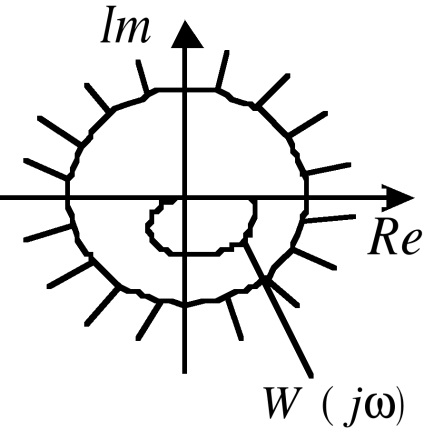
Voronov körkörös kritériuma egyszerűbb az alkalmazásban, de szigorúbb ("elégséges") feltételeket ad az abszolút stabilitásnak. Ezért célszerű alkalmazni, amikor vagy. azaz azokban az esetekben, amikor lehetetlen alkalmazni Popov kritériumát.
5. Robusztus stabilitás
Az abszolút stabilitás, amint azt fentebb megjegyeztük, azzal a kívánsággal társul, hogy figyelembe vegyék a dinamikus rendszer modellben a nemlinearitások leírásában felmerülő bizonytalanságokat. Általában azonban a lineáris elemek bizonytalanságokat is tartalmazhatnak, mivel a modellek paramétereit néhány hibával is meghatározzák. Ennek kapcsán bevezetik az úgynevezett robusztus stabilitást az ellenőrző rendszerek számára.
A rendszerparaméterek, például az időállandók vagy az átviteli tényezők meghatározásának bizonytalansága azt jelenti, hogy ezeknek a paramétereknek a pontos értékei nem ismertek. Valójában mindig is ismert, hogy ezeknek a paramétereknek az értékei bizonyos határokon belül vannak. Hangsúlyozzuk, hogy maguk az együtthatók. A rendszer időállandói és egyéb paraméterei állandónak számítanak.
Ez azzal a ténnyel jár, hogy például a szabályozási rendszer különböző modelljeinek jellemző polinomjainak és egyéb paramétereinek együtthatói tekintetében csak azok az intervallumok ismertek, amelyekben az értékük ismert.
Például a jellemző polinom együtthatói
a lineáris rendszer kapcsolatokkal adható meg
Az így megadott együtthatók nevezhetők intervallum együtthatóknak és a különbségnek # 150; időközönként. A felső és az alsó értékek a csúcson vannak kiszámítva. és alacsonyabb. az együtthatók értékeit. intervallummatematikai módszerek [22].
Az n-edik sor interpolációs polinomiáját általában az alábbiak szerint írjuk le
A technikai alkalmazásokban a különböző hibák és bizonytalanságok leggyakrabban relatív hiba alapján határozhatók meg. Ezért a karakterisztikus polinom együtthatóit gyakran a számított értékek adják. talált valamilyen relatív hibával%, azaz. Az együtthatók e specifikációjával a felső és alsó értékeket a nyilvánvaló összefüggések határozzák meg:
Ebben az összefüggésben feltételezzük, hogy a vezérlőrendszer jellemző polinom (11) együtthatóinak felső és alsó értékeit adjuk meg. A relatív hibák% lehetnek azonosak minden együtthatókra, azaz.
Definíció. Dinamikus rendszer jellemző polinommal (11) stabilan stabil. ha az állandó együtthatók bármely értéke tekintetében aszimptotikusan stabil egészként. a (10) intervallumoktól.
Az intervallum paraméterekkel rendelkező rendszerek robusztus stabilitásának értékelése céljából általában a VL által javasolt kritériumot használják. Kharitonov [22]. Ez a kritérium lehetővé teszi a dinamikus rendszerek robusztus stabilitásának tanulmányozásával kapcsolatos problémák csökkentését az egyes polinomok Hurwitz-tulajdonságának vizsgálatához. Ebből a célból először a következő formájú négy Kharitonov polinomot állítják össze:
Mindegyik polinom foka polinom foka intervallum (11), és ezek az együtthatók egyenlő intervallum határát az együtthatók e polinom.
Kharitonov kritériuma. Dinamikus rendszer intervallum jellegű polinommal (11) stabilan stabil, ha mind a négy Kharitonov polinom (13) Hurwitz polinom. ■
Így bizonyos rendszer robusztus stabilitásának vizsgálata intervallum paraméterekkel. Meg kell találni egy intervallum karakterisztikus polinomja a rendszer formájában (11), majd hozzon létre négy polinomok Kharitonov (13) annak ellenőrzésére, hogy azok megfelelnek a kritériumnak Hurwitz és Routh.
3. példa Vizsgálja meg egy rendszer polinóma robusztus stabilitását
A megoldás. A Kharitonov polinomok ebben az esetben a forma
Ebben az esetben a Kharitonov polinomok mértéke. ezért
A Hurwitz-kritérium helyett Vyshnegradskii aszimptotikus stabilitásának kritériumát alkalmazhatjuk.
Emlékezzünk vissza, hogy megfelelően a kritérium Vyshnegradsky harmadik fokú polinom Hurwitz, ha minden együttható nagyobb, mint nulla, és a terméket az ő „átlagos” együtthatók nagyobb, mint a termék a „szélsőséges” együtthatók.
Ezt a kritériumot a polinomokra (14) alkalmazva megállapíthatjuk, hogy ebben az esetben mind a négy Kharitonov polinom (14) Hurwitz polinom. Következésképpen a vizsgált rendszer stabilan stabil. ■
Vegyünk egy konkrét példára a harmadik rendű rendszer robusztus stabilitásának becslésére vonatkozó problémát, amikor meghatározzuk a paraméterek relatív pontosságát.
4. példa: Értékelje a rendszer polinómikus stabilitását
5% és 2% -a hiba végrehajtása az együtthatók.
A megoldás. Az együtthatók pontos (számított) értékei esetében az adott rendszer nyilvánvalóan aszimptotikusan stabil. Valóban, minden polinom együtthatóit (15) nagyobb, mint nulla, és a termék az ő „átlagos” együttható egyenlő 186, hogy több munka „extrém” tényező egyenlő 160. Ezért, összhangban a kritériumnak Vyshnegradsky rendszer stabil.
Ha az együtthatókat 5% hiba mellett hajtja végre, a (12) szerint az intervallumok határértékei:
Következésképpen a vizsgált rendszer interpolációs polinomiája ebben az esetben van kialakítva
és a megfelelő Kharitonov polinomokat
Ebben az esetben az első, a második és a negyedik polinom megfelel a Vyshnegradskii kritériumnak, és a harmadik # 150; nem felel meg, mivel 2,8558,9 = 167,865 és 8,421 = 176,4.
Így, ha az együtthatókat 5% -os hiba mellett hajtják végre, a vizsgált rendszer nem robusztus stabil.
Az együtthatók 2% -os hiba esetén történő végrehajtásakor az intervallumok határértékei:
és a megfelelő Kharitonov polinomokat
Ebben az esetben a Vyshnegradskii kritérium egyenlőtlenségei: 185,93> 159,94; 185,93, 159,94; 178,63> 166,46; 193,15> 153,64.
Így a 2% hibával rendelkező együtthatók megvalósításával mind a négy Kharitonov polinom megfelel a Vyshnegradskii kritériumnak, ebben az esetben a vizsgált rendszer robusztus stabil.
Az abszolutizmus egyértelműen kifejezett korszakának Angliában való hiánya, például Franciaországban; a parlament létezése az angol abszolutizmusban; kompromisszum és befejezetlen jellege az Állami Egységes Vállalkozás brit polgári forradalmának; folytonosság a fejlesztés állami intézmények engedélyezett burzsoá történészek és gosudarstvoved tulajdonított a megjelenése az alkotmányos rend angliai XIII XV században tagadni a létezését időszak abszolutizmus az országban kezelik az angol polgári forradalom a tizenhetedik században. mint alkotmányos-vallási konfliktus.
A rendszer tulajdonsága, hogy a perturbáció eltávolítása után kezdeti állapotba kerüljön, stabilitást jelent. A stabilitási kritérium egy olyan szabály, amely lehetővé teszi egy rendszer stabilitásának meghatározását a jellemző egyenlet gyökereinek kiszámítása nélkül.