Prime számok
Először egy rövid elmélet.
Az egyszerű számok olyan természetes számok, amelyek csak önmagukban és egyenként oszthatók. 2,3,5,7,11,13,17,19,23,29.
A legfontosabb nehézség az elsődleges számok, hogy nem olyan könnyű megtalálni, amikor a gigantikus jelentések. Minden, mert nincs elegendő egyszerű képlet a számításuk érdekében. Például a legnagyobb talált prímszám 22,338,618 számjegyű, térfogatban ez durván 7 kötet háború és béke.
Néha nincs mit csinálni, megpróbálok olyan formulát találni, amely elsőszámú számokat találna, de így van, de ez olyan, mint az agy rágógumi, ez használhatatlan, de az agy gondol, gondolja. És mégis, talán úgy tűnik, megtalálta a módját, ha egyszerűbbnek találja ezeket a számokat. A "talán" szavak azért vannak, mert hiányoznak a matematikai és számítástechnikai ismeretek ahhoz, hogy ezt ellenőrizhessem, ezért meg akarom osztani azt, amit én. Tud-e bárki képes megfogalmazni az ötletemet és ellenőrizni ezt a módszert?
Általában a beosztás lényege. Úgy döntöttem, hogy a banális szekvenciát a prímek egyes szekvenciáiból származtatják, és azt tabletták formájában írják, ahol minden prímszám szekvenciája a következő: 2 = (1,2,1,2,1,2) 3 = (1,1, 2,1,1,2,1,1,2) 5 = (1,1,1,1,5,1,1,1,1,5,1,1,1,1,5) És stb Először kiderült, hogy egy ilyen tabletta.
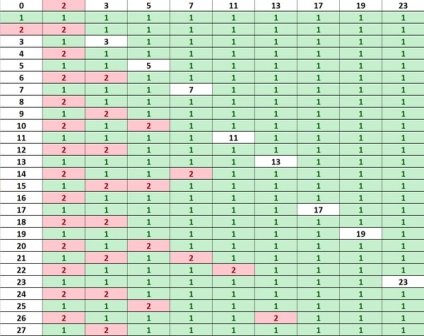
Kiderült, hogy a sorok, ahol minden "1" egy új főszám. A lemezt egy kicsit egyszerűsítették, 1-től 0-ig, 2-től 1-re, elvben, anélkül, hogy bármilyen különbség lenne a sorrendben (1,1,2,1,1,2) vagy (0,0,1,0,0,1) , úgy tűnt, hogy ez könnyebb lesz. És eltávolították a 2-es és a páros számokat, mert még mindig nem esnek páros szám alá.
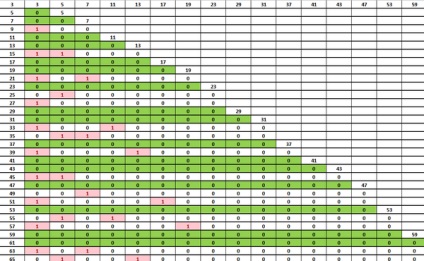
Elvileg ez a táblázat mutatja a nyilvánvaló dolgokat, három - minden harmadik számot oszt, ötöt - minden ötödik, hét - minden hetedik. de egyértelmű, hogy megtalálja a következő prímszám, elég, hogy ott csak a 0 vonal, és talán azt is, hogy egy olyan (van egy hasonló, de van a szekvenciák a kereszteződés), de attól még nem lesz értelmetlen, mert a nagyszámú számítás lesz végtelenül hosszú.
Egy másik dolog az öntapadósík. Úgy tűnik számomra (és talán csak úgy tűnik, és nem vagyok igaza), hogy olyan programot készíthet, amely kiszámítja az ilyen tablettát, mert itt elvileg nincs külön számítás. Nagyon könnyű szekvenciák vannak, akkor valószínűleg olyan programot állít be, amely az 1. számú számot az oszlopba írja a 0 helyett, és ellenőrizze a sztringet, ha mindenhol 0, akkor új oszlopot állít be. Igen, nagy számok esetén hihetetlenül nagy mennyiségű adat lesz, de például ugyanazon elsőszámú 22 338 618 számjegyre, két évre volt szükség ahhoz, hogy meggyőződjön az egyszerűségéről.
Általában én csak nagyon kíváncsi, hogy vajon lehetséges, hogy egy táblázatot, amely kiszámítja, hogy önmagát? (Ha nem, akkor sajnálom, hogy időt), és ha igen, vajon nem lenne egy gyorsabb utat kiszámításához prímszámokat?
Talán vannak a pikabushnikov: matematikusok, programozók, akik ellenőrizhetik.
1. Készíthet "asztalt".
2. Gyorsabb nem - még egy triviális vizsgálati nagyszámú egyszerűsége brute force 2 szögletes ezt a számot (nincs értelme, hogy ellenőrizze, 2 és a szám - 1) és összehasonlítása a maradék osztály gyorsabb lesz, mint táblázat kitöltése. A Luke-Lemer teszt, egyszerűen hozzáadásával n + = 2-nek még gyorsabbnak kell lennie. De valószínűleg el kell távolítani a teszteket - csak akkor kell egy szabad operációs rendszerrel meghatároznunk (megértjük, hogy egy fájlból származó sorok értékének megértése többször is fékezi a folyamatot).
Ha azt szeretnénk, hogy - segíthet a kódot Python * ez érdekes számomra, * és B * majd számtani kellene dolgozni egy kicsit gyorsabb * (magyarázattal, hogy mi folyik itt, hogy vége lenne, akkor írj magad). Az excel-a-ból azonnal el kell menni, t. hogy fékezze magát az irodában és megfelelően becsülje meg a számítás idejét az asztal alatt, és keressen rá nem lehetséges.
Ui Feliratozom a postára - érdekes volt olvasni.
Bontsa ki a 0-as fiókot
Valami azt mondja, hogy ez nem egy "algoritmus", hanem egy egyszerű megjelenítés a "főszám" fogalmának.
Bontsa ki a 0-as fiókot
Általában hallottam, hogy a prímszámok bizonyos kapcsolatban állnak a Fibonacci-számokkal
Bontsa ki a 0-as fiókot
Van valami furcsa "egyszerűsítés" a természetes szám kanonikus formájáról.
Nyilvánvaló, hogy ha egy kanonikus formában csak egy szám van, akkor az elsődleges