Példák az izometrikus és a dimetrikus vetületek konstrukcióira, leíró geometria
Az alábbiakban néhány példát találunk a téglalap alakú izometrikus és a dimetriai vetületek szerkezetére.
I. A gömb vetítése. Az 1. ábrán. A fenti 473. Ábrán egy gömb képe látható az izometrikus és a dimetriai vetületekben.
Mindkét esetben a gömb egy nyolcadik kivágással látható. A vetület vázlatát ábrázoló köröket rajzolták: egy izometrikus vetület, amelynek sugara egyenlő
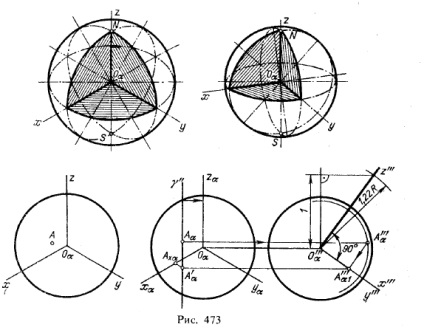
1.22R, az 1,06R sugár sugárú dimetrikus vetület esetén, ahol R a gömb sugara. Az ellipszisek mindkét esetben megfelelnek az equatoriális és a két meridional keresztmetszetnek.
A 473. ábrán bal alsó részében a gömb képét izometrikus vetületben mutatjuk be; a látható oldal a gömbnek A. pontban jobbra látható az építőiparban a másodlagos nyúlványok A'α (lásd az ábrát 449), és egy háromszintű koordináta vonallánc Aa A'α Ahα Oα. amely lehetővé teszi az A pont téglalap alakú koordinátáinak térbeli meghatározását. Építőipari tette a feltételezést, hogy a sík izometrikus vetítési foglal egy elülső helyzetét, és hogy ravnonaklonennyu hozzá tengely x, y, z derékszögű koordinátái vetített nem csak erre a síkra, hanem a járulékos profilozott síkban π3. Rendszer fordul vetítési síkok α, π3 és vetületi Aa-és A „„α előre meghatározott ponton az A, és A”" α alkalmazásával kapott gömbök szekcionált op. γ. Az A pont másodlagos vetülete szintén két vetület: A '' α1 és A'α
2. A henger és a kúp metszésvonalai egy síkban. A 474. és 475. ábra a henger és a kúp metszésvonalainak izometrikus vetületeinek elrendezését mutatja előre tervezett síkokkal. A vizsgált esetekben a metszésvonal ellipszis.
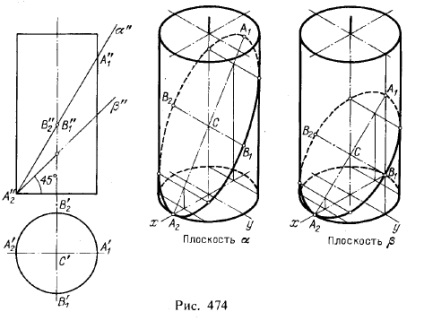
Először is, a rajz alapján, az A1 és A2 pont koordinátáit ábrázoljuk az α és β síkok lejtős vonalaival. Az ellipszis pontok felépítéséhez a segéd szekvenciákat vesszük: a henger - párhuzamos a generátorokkal és a yOz síkkal - a kúphoz -
1) Az építést a csökkentett torzítási együtthatókban hajtják végre.
A csúcson az y tengellyel párhuzamosan halad. Ezeket a síkokat az y-tengellyel párhuzamos, a henger és a kúp alapjainak síkjai adja.
Ezzel a segéd síkok választásával az a és β síkokat metsző egyenes vonalakat a γ tengellyel párhuzamosan nyerik. Az ellipszis pontjai e vonalak metszéspontjában a henger és a kúp generátorával kaphatók.
Először is olyan jellegzetes pontokat kell találnunk, amelyeket a rajzokon az A1 betűkkel jelölünk. A2. B1 és B2. és a vázolt vonalakon kapott izometrikus vetület. A szakaszban kapott ellipszis semimajor tengelye egyenlő C'B'1 értékkel. szintén megőrzi értékét az izometrikus vetületben (C'B'1 = CB1). Az izometrikus vetület ellipsziséhez tartozó kis tengely értéke azonban csak a m-re képes megtartani a B1 B2 szegmenst. β, vagyis az ábrán jelzett sík dőlésszöge 45 °.
Valójában ebben az esetben az Y tengellyel párhuzamos B1 B2 szegmens is az A1 A2-re merőleges izometrikus vetületben marad. következésképpen az A1 A2 és B2 B2 szegmensek megtartják az ellipszis tengelyük értékét. Abban az esetben, ha a sík más hajlásszöge van, amint azt a hengeren pl. α, az A1 A2 és B1 B2 szegmensek az izometrikus vetületben nem az ellipszis tengelyei, hanem csak a konjugátumátmérők vannak.
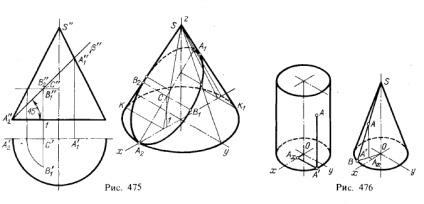
3. A koordinátaszegmensek építése egy henger felületén meghatározott pontra és egy tengelyirányú kúpos kúpra. Az 1. ábrán. 476 példákat mutat be egy hengerre és egy kúpra izometrikus vetületben. Minden esetben az eredet az alap középpontjában van (O pont).
A z tengely mentén egyenes vonalat húzunk a henger A pontján, és az A 'másodlagos kivetítésből egy egyenes vonalat húzzunk párhuzamosan az y tengelyre, amíg az az x tengelyt metszi. A 0Ax szegmensek. Ax A 'és A'A lehetővé teszik számunkra, hogy meghatározzuk az A pont koordinátáit egy adott koordináta-tengelyrendszerben.
A kúppal ellátott A ponton egy generátort állítanak elő, és ennek a generátornak egy másodlagos vetülete (OB) van kialakítva. Az A ponthoz merőleges rajza az OB-vel való metszésponttal az A pont másodlagos vetületeit kapjuk.
Az 1. ábrán. A 477 ábra egy koordináta-szegmensek felépítését mutatja a csonka kúp felszínén meghatározott ponton izometrikus vetületben (411, a ábra). Tegyük fel, hogy a kúp egy része a tengelyen áthaladó síkban van
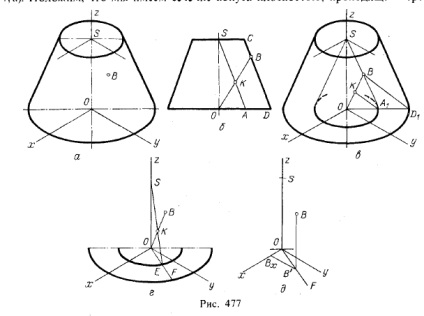
kúp és a B pont (477.6 ábra). A kapott trapéz alakban a SA || vonal CD-t és az OB vonalat, amely a K ponton áthalad. Rendben van. KB = OA. AD. De ez az arány az izometrikus vetületben marad. Az S ponthoz és a csonka kúp generátorával párhuzamos generátorhoz egy csúcsot állítunk össze (477. ábra, c). A
OA1 viseléssel. Az A1 D1 megismétli az OA arányt. AD, a fenti arányban. Most megkaphatjuk a K pontot az OB-ban a 2. ábrán. 477, c. Generátor, át húzott pontok S és E, meghatározza a K pont (ábra. 477 g), és a nyúlvány alkotó OF, amely az a pont B. Ebből képesek vagyunk, hogy kap egy másodlagos nyúlvány B „(ábra. 477, stb), és a koordináta szegmensek BB ', B'Bx és OBx. a z, y és x koordinátái.
Abban az esetben, ha a csonka kúpot nem lehet teljes egészében elvégezni, akkor ezt a szerkezetet kell megadni. Ha befejezhetjük az építést, akkor az építtetést végezzük el, amint az a 2. ábrán látható. 477,6.
4. Példák a hengeres és kúpos felületek metszésvonalainak kialakítására egymással. A metszésvonalak pontokból állnak; ezek a pontok vagy az ortogonális vetületekből vett koordinátáik, vagy a segéd szekvenciák közvetlen tengelymetriás kiálló részeiben találhatóak. Ez utóbbi az 1. ábrán látható. 478, a -
A segéd szekvencia síkok metszi ezeket a hengereket és a kúpokat a generáló vonalak mentén. Az 1. ábrán. 478, és a hengerek tengelyei metszik egymást, az 1. ábrán. b) keresztezés. Ha a 3. ábrán látható. a) az A és A1 pontokat egy mindkét henger tengelyein átmenő szekvenciasík alkalmazásával határoztuk meg, majd a 2. ábrán. b) figyelembe kell venni a
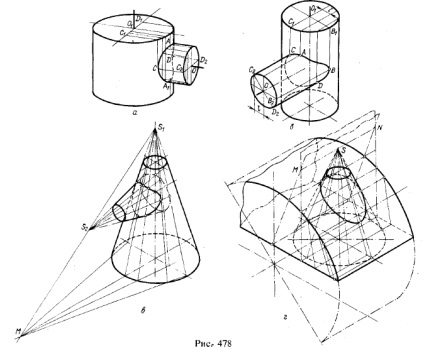
l 1). Az 1. ábrán. 478, a vágási síkban áthaladnak az S1 S2 vonalon. és ezek nyomai a kúp alapja síkjával az S1 csúcson áthaladnak az S1 S2 vonal nyomvonalán ezen a síkon. Az 1. ábrán. 478, r a sík áthalad az MN vonalon, amely a kúp csúcsán áthalad - az S pont, párhuzamosan a henger generátorával.
1) A pontok betűkkel való megjelölése csak magyarázatra szolgál.
5. A kör érintkezési pontjainak kialakítása - a gömb vetületének vázlata - ellipszis - a gömbön kapott kör vetülete, amikor síkban metszik. Az 1. ábrán. 479, és a három sík által elvágott gömb - profil (γ), vízszintes (δ) és elülső (β) látható. E rajz szerint egy izometrikus vetületet (479.6 ábra) állítanak elő a csökkentett torzítási együtthatókban. Az ellipszis m az 1. ábrán látható módon van kialakítva. 469, és az ellipszis n - ahogy az 1. ábrán látható. 465. A gömb vetületét egy körvonallal jelöljük - egy sugár sugara egyenlő az 1.22R értékkel. Ez a kör megérinti az ellipszist m a K ponton, az ellipszis n - a L ponton.
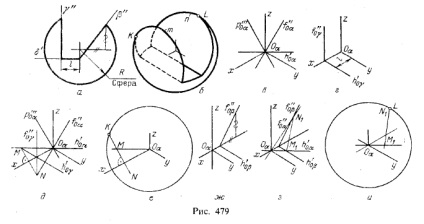
Figyeljük meg, hogy miként találtuk meg a K pontot, amelyet egy körön - a gömb kivetítésének vázlata, vagyis az izometrikus vetület (α) síkjában és egyben az ellipszis m-ben, vagyis a négyzetben. γ a gömböt átlépve. De ha a pont egyidejűleg két síkhoz tartozik, akkor ezek a síkok metszéspontja.
Az izometrikus vetület síkja ugyanolyan hajlamos arra, hogy π1. π2 és π3. A sík nyomainak háromszöge egyenlő oldalú (lásd a 457. ábrát). A pl. α az Oα pontig. vagyis a tengelyek elejére és a gömb középpontjára, akkor a 3. ábrán jelzett sávok helyzetét szenvedjük. 479, c.
Pl. γ az ugyanazon tengelyek rendszerében a pályákon látható, ahogy az a 2. ábrán látható. 479, g. Kompatibilis a. c) és a d) és a kivitelezést metszésvonal síkok a- és γ (ábra 479, e). MN vonal áthalad az M pont a metszéspontja a vízszintes nyoma követő párhuzamos p „„0α mivel a y || π3 (ahol P.” '0α ⊥Oα X. Ezért MN⊥Oa x).
Most pedig meg kell találni a K pontot az MN vonal metszéspontjával a körhöz - a gömb izometrikus vetületéhez (479, e).
Az L pont helyzetének meghatározásához (lásd a 479., b) ábrát, az izometrikus tengelyek rendszerében elölről kiálló síkot kell ábrázolni. β (ábra. 479 g) A, majd megtalálják a metszésvonal síkok a- és β (ábra. 479, s), ez a vonal áthalad a metszéspontja M1 és h'0α h'0β nyomok és ezen keresztül a metszéspont N1 pályák f " 0β és f "0a. Keresek pont L kapjuk meg a kereszteződés egy egyenes vonalat a kör M1 N1 - izometrikus vetülete egy gömb (ábra 479, és a.).