Az algebrai frakciók hozzáadása és kivonása különböző nevezők, a legnagyobb tanulmányi portál
Különböző denominátorokkal rendelkező algebrai frakciók hozzáadása és kivonása
Különböző denominátorokkal rendelkező algebrai frakciók hozzáadása és kivonása
Összeadás és kivonás az algebrai törtek különböző nevezők működnek ugyanazt az algoritmust, hogy használják az összeadás és kivonás frakciók különböző nevezők: első frakciók elvezethet a közös nevező a megfelelő kiegészítő szorzó
teley majd összeadást vagy kapott frakciókat ugyanazzal a nevező által a jogállamiság § 3. Lehetőség van megfogalmazni egy algoritmus kiterjed minden esetben az összeadás (kivonás) az algebrai törtek.
Algebrai frakciók hozzáadása (kivonása) algoritmusa

Példa 1. Művelet végrehajtása:
A megoldás. Az itt megadott pár algebrai frakciók mindegyik fajtájára a fenti 2. példában találjuk a közös nevezőt.
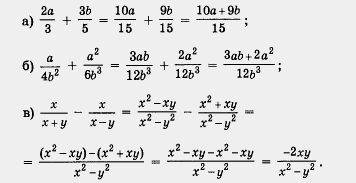
A fenti algoritmus legnehezebb pontja természetesen az első lépés: egy közös nevező megtalálása és a frakciók öntése egy közös nevezőre. Az 1. példában előfordulhat, hogy nem tapasztaltál ezt a nehézséget, mivel az eredményeket a §2-ben használtuk.
A közös nevező megtalálására vonatkozó szabály kidolgozása érdekében elemezzük az 1. példát.
A frakciók esetében a közös nevező a 15-ös szám, a 3. és az 5. részre oszlik, a közös többszörös (még a legkisebb közös többszörös).
A frakciók esetében a közös nevező a 12b 3 monomium. Mind a 4b 2, mind pedig a 6b 3-ra van osztva, azaz mindkét monomiális, amelyek a frakciók nevezőként szolgálnak.
Megjegyzés: a 12-es szám a 4 és 6 számok legkisebb közös többszörözője. A b változó szerepel az első frakció nevezőjében a 2. exponenssel, a nevezőben
második frakció - a 3. kitevővel. Ez a 3-as mutató legnagyobb értéke a közös nevezőben.
A frakciók esetében
A termék (x + y) (x - y) közös nevezõ, az x + y nevezõvel és az xy nevezõvel osztható.
A közös nevező megtalálása során természetesen minden nevezőt faktorizálni kell (ha ez nem volt kész állapotban). És további munkát vállalt szakaszból áll: hogy megtalálják a legkisebb közös többszöröse a numerikus együtthatók (utalva az egész együtthatós) meghatározza az egyes többször találkozott szó faktor legnagyobb kitevő, tedd az egészet egy darabban.
Most elkészítheti a megfelelő algoritmust.
Algoritmus a közös nevező megtalálásához több algebrai frakcióhoz

Mielőtt továbblépne, próbálja meg alkalmazni ezt az algoritmust az 1. példában szereplő algebrai frakciók közös nevezőjének megtalálásához.
Megjegyzés. Valójában két algebrai frakciónak van ugyanannyi közös nevezője. Például a közös frakciók esetében
a nevező lehet 30, és több 60, sőt akár egy 15a2b monomiális is. Az a tény, hogy a 30, a 60 és a 15a 2 b mind a 3-as, mind pedig a 5. részre osztható
frakciók -
közös nevezõ, kivéve a fent leírt 12b monomiát. lehet mind a 24b 3, mind a 48a 2 b 4. Ugyanaz a 12b 3 monomi jobb, mint a 24b 3., mint a 48a 2b 4. Egyszerűbb (formában). Ezt néha még egy közös nevezőnek sem nevezik, de a legkisebb közös nevezőnek. Így a fenti algoritmus egy algoritmus
több algebrai frakció legegyszerűbb közös nevezőjének megtalálása, algoritmus a legkisebb közös nevező megtalálására.
Ismét visszatérünk az 1. példához, a. Algebrai frakciók hozzáadásához. nemcsak egy közös nevezőt (15-ös szám) kellett találni, hanem minden egyes frakció számára további tényezőket is meg kellett találni, amelyek a közös nevező részévé válnának. A frakció ilyen kiegészítő készletét
Az 5-ös szám a lakos (ennek a frakciónak a számlálója és nevezője 5-tel többszörösen multiplikált), a 3. frakcióhoz (ennek a frakciónak a számlálója és nevezője 3-mal szorozva).
A további tényező a közös nevező hányadosa, osztva ennek a törtnek a nevezőjével.
Általában használja a következő bejegyzést:
Ismét, menj vissza az 1.6. Példához. A közös nevező a frakciók egytagú 12b 3. A további tényező egyenlő az első frakciót Zb (mivel 12b 3. 4b 2 = H b), ez egyenlő 2 (például a 12b 3. 6b 3 = 2) a második frakció. Ezért az 1.6. Példa szerinti megoldás az alábbiak szerint formalizálható:
Az algoritmus több algebrai frakció közös nevezőjének megtalálására szolgáló algoritmust tartalmaz. De a tapasztalat azt mutatja, hogy ezt az algoritmust a tanuló nem mindig értette, ezért kissé módosított formulát adunk.
Az algebrai frakciók közös nevezőre történő csökkentésére vonatkozó szabály

2. példa: Egyszerűsítse a kifejezést
A megoldás.
Az első szakasz. Találjuk meg a közös nevezőt és a további tényezőket.
Van
4a 2-1 = (2a-1) (2a + 1),
2a 2 + a = a (2a + 1).
Teljesen az elsõ nevezõt veszünk fel, és a másodikból hozzáadunk egy faktort, amely nem az elsõ nevezõben van. Megkapjuk a közös nevezőt
Helyénvaló a rekordok táblázatos formában történő rendezése:
A második szakasz.
Végezzük el az átalakításokat:
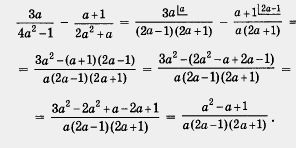
Bizonyos tapasztalatok jelenlétében az első szakasz nem osztható ki, és a második lépcsővel párhuzamosan végrehajtja.
Összefoglalva, vegyünk egy bonyolultabb példát (azok számára, akik szeretnének).
3. példa. Egyszerűsítse a kifejezést
A megoldás.
Az első szakasz.
Minden nevezőt bontunk multiplikátorokká:
1) 2a 4 + 4a 3 b + 2a 2 b 2 = 2a 2 (a 2 + 2ab + b 2) = 2a 2 (a + b) 2;
2) 3ab 2 - 3 = For (b 2 - a 2) = A (b - a) (b + a) esetén;
3) 6a 4 -6a 3b = 6a3 (a-b).
Először vesszük a nevező teljesen, a második veszi hiányzó szorzók 3 és b - egy (vagy a - b), a harmadik - a hiányzó faktor a (mivel a harmadik tényező, és a nevező tartalmaz 3).
Megjegyezzük, hogy ha a további faktor "-" jelzéssel van ellátva, akkor általában a teljes frakció előtt helyezkedik el, vagyis a második frakció előtt meg kell változtatni a jelet.
A második szakasz.
Végezzük el az átalakításokat:
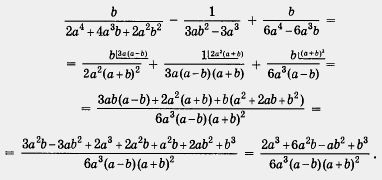
Megjegyezzük, hogy a 3. példában megadott kifejezés helyett az algebrai frakciót, amely az identitás transzformációját eredményezi a változók elfogadható értékeihez. Ebben az esetben az a és b változók bármely értéke elfogadható, kivéve a = 0, a = b, a = -b (ezeknél
a nevezők eltűnnek).