A leckét "a testek térfogatának kiszámítása határozott integráció segítségével"
A dokumentum rövid leírása:
TEXT LESSON NYILATKOZAT:
Ma a leckében egy test mennyiségének kiszámítására szolgáló képletet fogunk lefektetni egy meghatározott integrál segítségével, és a képletet a probléma megoldására alkalmazva.
Emlékezzünk arra, amit egy meghatározott integrálnak nevezünk.
Ha az f (x) folytonos a I valós tengelyének tartalmazó pont x = a és x = b, akkor a különbség értékek F (b) -F (a) (ahol F (x) - a primitív f (x), hogy I) a f (x) függvény egy meghatározott integrálját nevezzük a-b-ból.
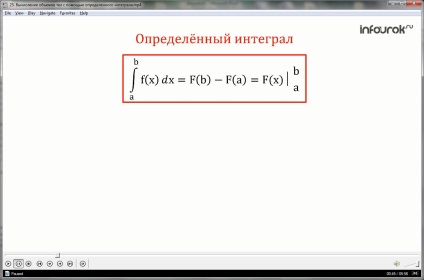
Ezt a képletet Newton-Leibniznek hívták.
(az ix deix-től az a-b ef integrálja megegyezik a Be-ből származó antiderivatív ef nagy értékeinek különbségével és a)
Származhat kiszámításának képlete az alaptest térfogatának koncepciója alapján az integrál: térfogata a test megegyezik a szerves egy B lábnyom alakú de X,
Vegyünk egy olyan önkényes testet, amely két egymással párhuzamos sík között van, amely merőleges ezekre a síkokra.
a és b a tengely tengelyének metszéspontjainak abszcisza ezekkel a síkokkal (a
Tekintsük egy adott test keresztmetszetét a tengelyre merőleges síkra. ebben az esetben Φ (χ), ezt a számot kör vagy sokszögnek tekintjük. Ezt a S (x) = S () értéket jelöljük. Ezután el kell osztanunk az [a; b] intervallumot n részekre. Bevezetjük a jelölést: ez az. b ez az. A távolság egymástól egyenlő lesz
A delta x összesen egyenlő az a és b közötti különbséggel.

Ezután vegye figyelembe a két ilyen sík között nyert testet. A szegmensek megtörik a testet n testekbe.
Tekintsünk egy testet, amelyet úgy kapunk, két ilyen sík T. térfogata ez a test megközelítőleg egyenlő a térfogatának a prizma, azaz lábnyom ábra szorozva delta x magasság itoe (ebben a szegmensben hossz)
Majd a térfogatot a teljes test közelítőleg egyenlő az összeg az ilyen szervek T, azaz, az összege i egytől n térfogatrész szervek, azaz a összege EK x itoe a Delta X itoe, miközben feltételezzük, hogy ES x itoe egy folytonos függvény az [a, b]
A határérték ez az összeg megegyezik a mennyiség a test, hanem azért, mert ez a határ az integrál összeg, ez egyenlő az integrál egy b-es x Te x.

Így kaptunk egy képletet az önkényes test térfogatának kiszámítására a merőleges szakasz területén keresztül. A test térfogata megegyezik az x-os bázis területének a-tól b-ig terjedő integráljától
Találjuk meg a testek kötetét a kapott képlet felhasználásával.
Find térfogata a test az ábrán látható, amikor ezt a testet a rész merőleges síkban az x-tengelyre, és áthalad a ponton abszcissza x, egy négyzet, amelynek oldalon egyenlő.
Adott: szekció négyzet
Megoldás: fontolja meg a rajzot
Az általunk levezetett képlet alapján a test térfogata megegyezik az x de x-től
A négyzet négyzetét a képlet keresi
S (x) =. akkor x egyenlő a négyzet oldalának négyzetével, helyettesítjük egy x-vel osztva a -ra. kapunk
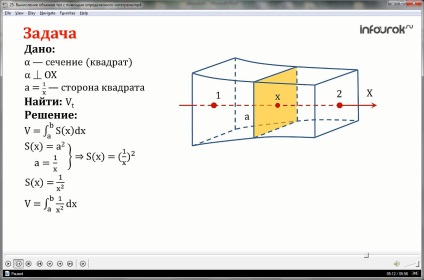
Behelyettesítve ez az érték a képlet megtalálásához a hangerőt egy határozott integrált: a test kötet határozott integrál A-ból B B a nyolcadik teljesítmény Te x
Primitív teljesítményfunkció
Ezután (1) válik: térfogata a test megegyezik a szerves 1 és 2 egység osztva négyzetével X TE X, egyenlő mínusz egy osztva x 1-2, helyettesítse az érték a maximális integráció két és egy, megkapjuk 0,5.