Vasilisa javiks - szellemi keresőmotor 1
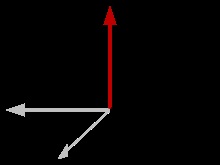
Az inverzió után a két vektor megváltoztatja jelét, de vektorterméke változatlan marad.
Axiális vektor (axiális középvonala Engl ..) vagy pszeudo - mennyiség, amelynek az összetevői alakítjuk a vektorral forgatások a koordináta-rendszer, de ez előjelváltása ellentétes a viselkedését a komponenseket a vektor bármely inverzió (jele forgalomban) koordináták. Ie A pszeudovektor megfordítja irányát, miközben megőrzi az abszolút értéket (többszöröse mínusz egy) a koordinátarendszer bármilyen inverziójára.
Annak érdekében, hogy hangsúlyozzuk a jelen vektor különbségét, amelynek koordinátáit mindig ugyanolyan módon transzformáljuk, mint az elmozdulásvektor koordinátáit, az igazi vektort valódi vagy poláris vektornak nevezzük.
A tengelyirányú vektor legegyszerűbb példája egy háromdimenziós térben két poláris vektor vektorterméke, például a mechanika, a szögsebesség # x00D7; . négydimenziós térben - egy axiális áram.
Alapvető információk
Amikor a koordináta transzformáció koordináta axiális kapott vektort megszorozzuk egy további faktor (-1), mint a valódi koordináta-transzformáció (amelyet más néven poláris) vektorok, ha alapján megváltoztatja a tájékozódás (például, ha a bázis van kitéve tükrös visszaverődés). Ez egy pszeudoscalárral együtt. egy pszeudotenzor különleges esete. A grafikusan ábrázolt pszeudovektor ezzel a koordinátájú változással megfordítja irányát.
- A geometriában a pszeudovektor leggyakoribb alkalmazása lehet egy háromdimenziós infinitezimális forgás segítségével történő reprezentáció. Valószínűleg (?), A kifejezés axiális vektor pontosan itt, mert ál határoz forgástengely (irányát), de csak egy faktor (± 1), az irányt a forgatás a kapcsolódó feltételes önkényes választás joga alapján, ellentétben igaz ( egy poláris) vektor, amely egy irányított szegmenset (vagy párhuzamos szállítást) képvisel, teljesen meghatározó és egyedülállóan meghatározza a kezdet és a vég pontjai.
A szokásos módon generálásának pseudovectors pseudovectorial ezt a műveletet, a leggyakoribb, ha nem az egyetlen általánosan használt háromdimenziós esetben az a vektor, a termék (például ami általában szokásos az a koordináta jelölést tartalmaz Levi-Civita ál) működését, és tartalmaz a vektor termék (például rotor, stb .) vagy páratlan számuk van. A pszeudovektor-művelet pseudovektorokat és pszeudo-skalarokat hoz létre valódi vektorokból és skalárisokból.
Így, ha az igazi vektort egy igazi vektorral megszorozzuk, akkor a skalár termékben és a vektor termékben a pszeudovektort az igazi skalárat kapjuk. Ha az igazi vektort egy pseudovektorral megszorozzuk, a pszeudoszkóport a skaláris termékben és a vektor termékben lévő vektortermékben kapjuk meg. Két pszeudovektor megszorzásával megkapjuk az igazi skalár és pszeudovektort.
A fizikai elmélet, kivéve azokat, amelyekben van egy külön, és megfigyelhető elvileg tükörszimmetrikusan teret pseudovectors lehetnek jelen a közbenső értékek, de a végső megfigyelt - szorzókat (-1) a tükörképe koordinátákat kell ártalmatlanítani, találkozó a munkálatok is (pszeudovektor + pszeudoscalár + egyéb pszeudo-tenzor faktorok száma).
- Például a klasszikus elektrodinamikában a mágneses mező indukálása pszeudovektor, mivel egy pszeudovektor művelet, pl. # x00D7; a Bio-Savar-törvényben. de ez az érték (pszeudovektor) alapvetően egy feltételes multiplikátorig, amely +1 vagy -1 lehet. Azonban a ténylegesen megfigyelt érték - a töltés mágneses mező hatására történő gyorsulása - a számításában egy másik pszeudovektor műveletet # x00D7; a Lorentz-erő kifejezésében. így egy másik feltételes tényező ± 1, megegyezik az első, a válasz az önkényesség eltűnik, mivel a termék ± 1 · (± 1) ad 1.
- A mechanikában a leggyakrabban előforduló pseudovektor a szögsebesség vektora és vele társult (például a szögsebesség). Az igazi sebességvektor a szögsebesség pszeudovektorából származik # x03C9; pseudovector működés # x03C9; # x00D7; .