Tesztes kérdések
1. Írja le a Lorentz erő kifejeződését vektoros formában.
2. Hogyan lehet meghatározni a Lorentz-erő irányát?
3. Hogyan fog a töltés egy egységes mágneses térben mozogni, ha a sebességvektor és az indukciós vektor:
a) párhuzamos, b) merőleges, c) 0 -7 Gn / m-es szögben helyezkednek el,
μ a mágneses átjáró mágneses áteresztőképessége,
N a mágnesszelep fordulatszámának száma,
A mágneses fluxus a mágneses szelep N fordulatán keresztül lesz
F = NBS = μμ0 (5)
ahol S a mágnesszelep keresztmetszete. Az (5) és (2) képletek összehasonlításával könnyen megtalálható a mágnesszelep induktivitása
Ha a mágnesszelep hossza összehasonlítható az átmérőjével, akkor a (6) képletbe egy korrekciós tényező kerül bevezetésre,
ahol a "K" egy korrekciós tényező, amely figyelembe veszi a mágnesszelep véges méreteit. (7) az is következik, hogy amikor a mágneses permeabilitás a közeg (), a töltési mágnestekercs változik annak induktivitása értékét. Ebben az esetben, amikor a mágnestekercs töitőközeget ferromágneses, loop induktivitás intenzitásától függ annak mágnesezettség, t. E. On egy áram, ami mágneses mezőt hoz létre a mágnesszelep. Ezért az L = f (I) ferromágneses mag jelenlétében és az L átlagolásával, amely különböző pontokban keletkezik, lehetetlen.
Induktivitás, kapacitás és ellenállás egy AC áramkörben.
Vegyünk egy olyan elektromos áramkört, amely az R ellenállásból, az L induktorból és a C kondenzátorból áll, és amelyhez egy külső EMF-et alkalmaznak, amely változik az ε (t) idővel. A törvény szerint
1. ábra Az áramkörhöz tartozó ohm írható:
ahol I a jelenlegi erő, R az ellenállás, ε (t) = εo * sinωt (εo a külső EMF maximális értéke, ω az oszcillációs frekvencia), εs. Figyelembe véve, hogy I = u =, a kifejezés (8) a következő formában írható:
Ez a másodrendű differenciálegyenlet az erőviszonyos rezgéseknek a figyelembe vételével történő ellenállását írja le. Ezen egyenlet megoldásával az aktuális intenzitás amplitúdójának kifejezését kapjuk:
Az expresszió (10) Ohm-törvénynek tekinthető a váltakozó áramra vonatkozóan. Ebben az esetben
- a váltóáramkör impedanciája, R - ohmos ellenállás, ωL - induktív ellenállás, 1 / ωс - kapacitív ellenállás, - gyakran reaktív ellenállásnak nevezik. Abban az esetben, ha nincs áramkör vagy kondenzátor az AC áramkörben, a kifejezés (10) egyszerűsödik, mert ebben az esetben RL = ωL vagy egyenlő nullával.
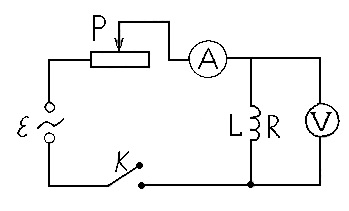
Vegyük figyelembe a 2. ábrán bemutatott elektromos áramkört, ahol P a dia-reosztát; L egy ohmos ellenállással rendelkező mágnesszelep; A - ampermérő, V - voltmérő, K - kulcs.
D
ahol I0 és U0 az ab szakaszban lévő áram és feszültség erősségének amplitúdója, R a solenoid ohmos ellenállása, RL = ωL a mágnesszelep induktív ellenállása. Az AC készülékek az amplitúdóértékekkel kapcsolatos tényleges áram- és feszültségértékeket a következőképpen mérik:
(a tényleges érték alatt, például egy váltakozó áram alatt, az egyenáram áramának nagyságát értjük, amely az ohmos ellenállásban ugyanolyan erősségű, mint a váltakozó áram). A fentiek alapján a (11) képlet a következő formában írható:
Megtalálni az Ieff eszközök segítségével. és Ueff. Meg lehet határozni az ab: láncrész impedanciáját:
Mivel az R ohmos ellenállás ismeretében megtalálható az L mágnestekercs induktivitása:
Itt = 6,28 * 50 = 314 (1 / s).
A munka teljesítményének sorrendje
Szerelje össze az áramkört a 2. ábrán látható módon.
Határozza meg az ampermérő és a voltmérő osztásának árát.
Távolítsa el a magot a tekercsről, kapcsolja be a "K" gombot.
Az áramkör aktuális áramának a reosztáttal történő változtatásával mérje meg az Ieff értéket. és Ueff. Mérés öt áramra és feszültségre. Jegyezze fel a mérések eredményeit az 1. táblázatban.
Megjegyzés: l (cm) a tekercsben lévő mag része.
A mérési eredmények feldolgozása
A (13) képlet segítségével kiszámolja az egyes mérések impedanciáját és adja meg az 1. táblázatban szereplő adatokat.
Számolja ki a mágnesszelep (14) képlet szerinti induktivitásának értékeit minden egyes mérésnél, és adja meg az 1. táblázatban szereplő adatokat.
Számítsd ki a mágnesszelep induktivitásának átlagát, az abszolút mérési hibát, az átlagos abszolút hibát és a relatív hibát. Minden számított értéket fel kell jegyezni az 1. táblázatban.
Ismételje meg az 1. és 2. pontban megadott számításokat a 2. táblázat adatai alapján.
Létre kell hozni egy grafikonot az L mágnestekercs induktivitás függésének függvényében a magnak a tekercsben való merülése mélységében l.
Formálja az elektromágneses indukció törvényét és a Lenz-szabályt.
Adja meg az önindukció jelenségének meghatározását.
Mi határozza meg az önindukció EMF nagyságát?
Adja meg a vezető induktivitásának és mértékegységének meghatározását.
Mi az induktivitás és az ellenállás szerepe egy AC áramkörben?
Hogyan határozható meg az induktív ellenállás, a kapacitív ellenállás és az AC áram impedanciája?
Az elvégzett munka eredményei alapján vonja le a következtetést a ferromágneses magnak a mágneses induktivitásra gyakorolt hatásáról.
Savelyev IV "Fizika tanfolyam", 2. kötet, 196-205., 272-284, 1989.
Detlaf AA Yavorsky BM Milkovskaya LB "A fizika tanfolyam", 2. kötet, 262-283. Oldal, 1977.
Kalashnikov SG "Villamosenergia", 179-192., 1977.
Laboratóriumi munka № 2.09
A NEMZETKÖZÖSSÉGI VESZÉLY HŐMÉRSÉKLETÉRE VONATKOZÓ TANULMÁNYA ÉS A WIDTH ZONE WIDTH MEGHATÁROZÁSA
A szilárd anyagok az ellenállásukban három nagy osztályra oszthatók: fémek (vezetők), félvezetők és dielektrikumok (szigetelők). Szobahőmérsékleten a különböző szilárdanyag-osztályoknál a értékek a következő határokon belül vannak:
Fémek 10 -8 10 -6 Ohm
Félvezetők 10 -6 10 8 Ohm
Dielektrikumok több mint 10 8 Ohm
Az ilyen tisztán kvantitatív osztályozás azonban nem közvetíti az elektromos vezetőképesség és a szilárd anyagok egyéb tulajdonságainak sajátos jellemzőit. A félvezetőktől a dielektrikumokig való átmenetben mutatkozó rezisztencia-változás hiánya inkább tükrözi alapvető kvalitatív hasonlóságukat. Jelentős minőségi különbség figyelhető meg a fémek és a félvezetők között. Például fémekben az ellenállóképesség növekvő hőmérsékleten lineárisan növekszik, és exponenciálisan csökken a félvezetőkkel (1.
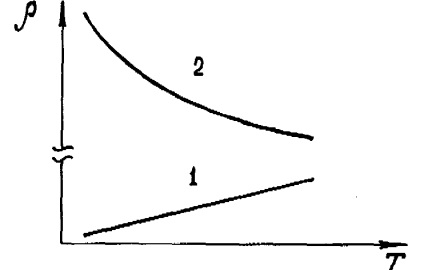
Ábra. 1. A fémek (1) és a félvezetők (2) ellenállásának hőmérsékletfüggése.
Az elektromos vezetőképesség és az osztályok egyéb tulajdonságainak különbségét magyarázza a szilárd anyag kvantummechanikai sáv-elmélete. A kvantummechanikából ismert, hogy bármely elszigetelt atomon az elektronok csak bizonyos diszkrét energiaértékekkel rendelkezhetnek, úgynevezett energiaszintek. És minden energia szinten, a Pauli-elvnek megfelelően, nem lehet több, mint két elektron. Az elektronokat a legmagasabb energiaszinten (elektronikus elektronikus pályák elektronjait) valence-elektronoknak nevezik. Ahogy atomokkal konvergencia távolságok egyenlő a inter-atomi távolságok szilárd, a kölcsönhatás a elektron kagyló atomok vezet az a tény, hogy az energia szintjét az egyes atomok hasítjuk, hogy létrehozzák a energia sávok a szilárd-test. Minden energia sáv egy tapintatlan dis-set, de nagyon szorosan tördelt energiaszintet, Num-lo, amelynek területe egyenlő a atomok száma a kristály, és a köztük lévő távolság körülbelül 10 -22 - 10 -23 eV (1 eV = 1.6 10-10 J).
Az energiatartománynak a valence-elektronokkal történő felosztásával létrejött energia zónát valence sávnak nevezzük. Az energiaszintet, amelyet az atom energia szintjének felosztása az energiaszint felett valenceelektronokkal felosztott, szabad zónának nevezzük. A valence sáv és a szabad zóna között tiltott zóna van. Itt nincs megengedett energiaérték. A szabad zóna fenekének és a valence sáv felszínének közötti energia különbség a tiltott zóna szélességének nevezik (az energia alsó része a zónában, a mennyezet a zónában lévő energia maximális értéke).
A szilárd anyagok elektromos vezetőképességét a valens sáv elektronikus töltésével és a tiltott sáv szélességével határozzák meg.
Attól függően, hogy a sávok mennyire töltik fel az elektront és a tiltott sáv szélességét ΔE, négy eset lehetséges, a 4. ábrán sematikusan ábrázolva. 2.
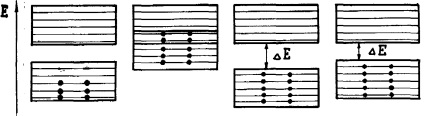
Ábra. 2. A fém (a, b), dielektromos (c), félvezető (d)
A valens sáv részlegesen fel van töltve elektronokkal (2a. Ábra). Ebben az esetben egy olyan elektron, amely önkényesen kis energiájú "adalékanyagot" kapott (például hőmozgás vagy elektromos mező miatt), magasabb energia szintre léphet ezen a zónán belül, és részt vehet a vezetőképességben. Ez a fémekre jellemző.
A valence zóna tele van, de átfedi a szabad zónát (2b. Ábra). Ebben az esetben az elektronok könnyen átvihetők a szabad zóna energiaszintjére és részt vesznek az elektromos vezetőképességben. Ez a fémekre jellemző.
Ezenkívül lehetőség van arra is, hogy a valens sáv teljesen feltöltődjön az elektronokkal és a szabad zóna üres legyen (2c. Ábra, d). A tiltott sáv szélességétől függően az ilyen sávszerkezetű szilárd anyagok dielektrikumok vagy félvezetők. Ha bandgap nagyobb termikus elektronok energiáját hőmérséklete határozza meg, az elektronok nem niÆljunk rAtE be egy szabad zóna (azaz, nem szerezhetnek további-edik hatványa, mivel az összes energia Államokban a vegyérték sáv foglalt, és hogy mozog a szabad zónában az elektronok hőenergia nem elegendő). Az ilyen kristály dielektrikum (2c. Ábra).
Végül, ha a sáv rés elég keskeny ahhoz, hogy elektronok átvitelét vegyértékelektronját egy szabad zóna megvalósítható viszonylag könnyen termikus gerjesztés, hogy egy félvezető kristály (ábra. 2g).
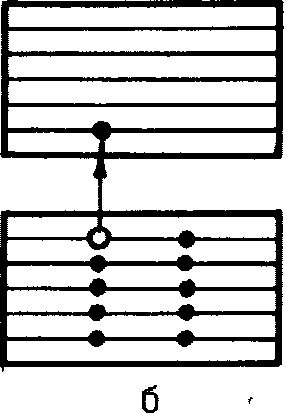
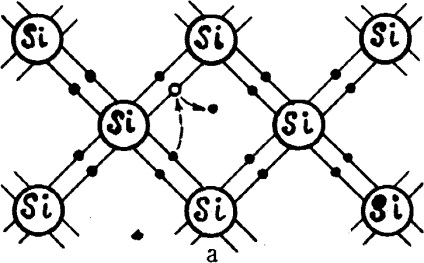
A félvezető az alapállapotú, amikor a vegyértéksávja (ez figyelhető meg viszonylag alacsony TEM-középhõmérséklete) a kristály nem szabad töltéshordozók, amelyek részt vesznek a vezetőképesség. Minden elektron kovalens kötésben van elfoglalva, amely az atomokat egy kristályrácsba köti össze. Ilyen körülmények között a félvezető semmilyen módon nem különbözik a dielektrikustól. Hőmérsékletnövelés mellett lehetőség nyílik arra, hogy egy elektront kivessenek ebből a kötésből. Ez képezi a szabad elektron, amely nem kötődik semmilyen adott atom kristályrácsba, és azon a helyen, ahol a kommunikációs alakult nyitott helyzetben, amely az úgynevezett egy lyuk (ábra. 3a). A nyelv a sáv elmélet, ez azt jelenti, hogy a hatása alatt termikus mozgás a elektronok leküzdeni a tiltott terület és mozgott a szabad zónában, és a lyuk van kialakítva (ábra. 3b) a vegyérték sáv.
E
Ha egy ilyen kristályt elektromos mezőbe helyeznek, akkor e téren a szabad elektron mozgatható, vagyis részt vesz az elektromos vezetőképességben.
Ábra. 3. Az ingyenes töltéshordozók képződésének rendszere a belső félvezetőben.
A szabad zónák elektronjai által végzett vezetőképességet elektronnak nevezik. Ugyanakkor eredményeként a termikus mozgás tud ugrani-vegyérték elektronok a szomszédos kötéseket a megüresedett - lyuk, és a lyuk jelenik meg a hely, ahol eltávozott elektron stb Egy külső elektromos tér hatása alatt az ilyen elmozdulások irányított karaktert mutatnak. Vagyis a vezetőképesség valenciaelektronokkal valósítható meg. Egy ilyen eljárás a töltés a furatok elektronok általában tekinthető a mozgás irányában a lyuk-SRI ellenkező elektron mozgás, mintha a lyuk-razziák adott pozitív töltés egyenlő nagyságú a töltési az elektron. A lyukak miatt a félvezetők vezetőképességét fúvóképességnek nevezik.
Így a félvezetőkben két vezetési mechanizmus figyelhető meg: az elektron és a lyuk. Ha az elektronok száma a szabad terület egyenlő a lyukak száma a vegyérték sáv, egy ilyen félvezető megfelelő és annak belső vezetőképességét. A saját félvezetők kémiailag tiszta félvezetők, amelyek magukban foglalják a Mendeleev elemek Si periódusos tábla IV. Csoportjának elemeit. Ge, valamint a III és V csoportok kémiai vegyületei, például GaAs, GaP és mások.
Ahogy a hőmérséklet emelkedik (azaz a termikus gerjesztési energia növekedésével), egyre több elektron fog mozogni a valensávról a szabad zónára, azaz nagyobb számú elektromos töltőhordozó (elektron és furat) alakul ki. Ez a félvezető elektromos vezetőképességének növekvő hőmérséklethez és ennek következtében az ellenállás csökkenéséhez vezet.
A félvezető-fizika elméletében kimutatták, hogy egy belső félvezető ellenállása a hőmérséklet függvényében változik a
ahol R0 egy bizonyos tényező a félvezető jellegétől függően;
k a Boltzmann konstans;
T az abszolút hőmérséklet.
Ebben a dokumentumban az (1) összefüggést használjuk a félvezető tiltott sávjának E szélességének meghatározására. Figyelembe véve a (1) kifejezés logaritmusát, megkapjuk
Az LnR és az 1 / T koordinátákban az (2) kifejezés az egyenes vonal egyenlete, amelynek grafikonját az 1. ábra mutatja. A (2) és a 4. ábrán látható, hogy a tiltott sáv szélességét a következő kifejezés határozza meg:
T
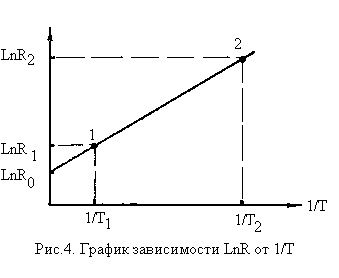
polgármester módon ellenállás mérésével a félvezető, a hőmérséklettől függően egy hőmérséklet-tartományban, ábrázoltuk LNR = f (1 / T), és kiválogatjuk a ez a grafikon értékek LnR2 és LnR1, megfelelő hőmérsékleten T2 és T1, lehet számítani a bandgap vizsgált félvezető. A gyakorlatban célszerűbb a tiltott sáv szélességét ábrázolni az LnR = f (10 3 / T) koordinátákban. Ebben az esetben figyelembe véve, hogy k = 1,3810 -23 J / K = 0,862-10 -4 eV / K. (1 eV = 1.610 -19 J), akkor a tiltott sáv szélességének kiszámításához a végső képletet kapjuk:
Kapcsolódó dokumentumok:
Laboratóriumi alkalmazásra való felkészítésre ajánlott; - olvassa el az előadási jegyzeteket és a tankönyv megfelelő szakaszait (képzés), töltse ki a bejegyzést. 7. a reakciótermékek visszavonása a reaktorból. Az NGP részecskék kölcsönhatásának fizikai-kémiai mechanizmusa.
Laboratóriumi alkalmazásra való felkészítésre ajánlott; - olvassa el az előadási jegyzeteket és a tankönyv megfelelő szakaszait (képzés), töltse ki a bejegyzést. a szilícium-dioxid rétegekhez képest a következő szilikonfilmeket biztosítja a szilícium-nitrid filmekhez.