Siklócsapágyak súrlódása és kenése
Súrlódási módok és számítási kritériumok. Megjegyeztük, hogy a súrlódási munka a csapágy munkaképességének fő mutatója. A súrlódás meghatározza a csapágy kopását és hőjét, valamint hatékonyságát. A súrlódás csökkentése érdekében a csapágyak kenve vannak. A csapágy működési módjától függően lehet félig folyékony vagy folyékony súrlódás is. E módok sematikus ábrázolása a 3. ábrán látható. 16.3.
Folyékony súrlódás esetén a tengely és a bélés munkaterületét egy olajréteg választja el, amelynek vastagsága nagyobb, mint a felületi érdesség magasságának összege (a 16.3. Ábrán az elválasztó olajréteget vastag vonal jellemzi):
Ebben az állapotban az olaj elnyeli a külső terhelést, megakadályozva a munkaterületek közvetlen érintkezését, azaz kopását. Ebben az esetben a mozgással szembeni ellenállást csak az olajréteg belső súrlódása határozza meg. A folyékony súrlódási tényező értéke 0,001. 0,005 (ami lehet kisebb, mint a gördülő súrlódási együttható).
Félfolyékony súrlódás esetén a (16.1) állapot nem figyelhető meg, a csapágyon pedig kevert súrlódás - folyadék és határ. A határt súrlódásnak nevezik, amelyben a dörzsölő felületeket vékony olajfilmmel borítják, amely az aktívolaj-molekulák és a bélésanyag molekuláris erőinek és kémiai reakcióinak eredményeként keletkezik. Az olaj határfelületi filmek (adszorpció) képessége tömegspektroszkópos,
flaxiness (tapadás, nedvesíthetőség). A határolófóliák stabilak és ellenállnak a nagy nyomásnak. A koncentrált nyomás helyén azonban elpusztulnak, a fémfelületek betétlapjainak tiszta olaja érintkezésbe kerül,
Az anyagrészecskék viszonylagos mozgással történő kialakulása és leválása. 1b. a csont súrlódását kísérik
Az orr dörzsölje felületét anélkül, hogy külső csiszolószemcséket kapna. A fél-folyadék-csont súrlódási együtthatója nem csak az olaj minőségétől, hanem a dörzsölő felületek anyagától is függ. A közös súrlódásgátló anyagokra a fél folyadék súrlódási tényezője 0,008. 0.1.
A csapágyak működtetéséhez a legkedvezőbb mód a folyadék súrlódási rendszere, amely a csapágycsúcsok többségének kiszámításához a legfontosabb kritérium a folyadék súrlódási rendszer kialakulása. Ugyanakkor a hatékonyságot az elhasználódás kritériuma határozza meg.
A folyékony súrlódás elméletének alapjai A csapágyak folyadék-csontsűrűségének vizsgálata a kenés hidrodinamikai elméletén alapul. Ez az elmélet egy viszkózus folyadék hidrodinamikai differenciálegyenletének megoldásain alapul, amely a nyomáshoz, sebességhez és egy adott nyíróerővel szembeni ellenállást társítja.
Az 1. ábrán. 16.4 ábra két plastinyAi 27, olajjal töltött, és siloyF.PlastinaAdvizhetsya betöltve a lemezhez képest 27 skorostyuVA.Esli skorostVAmala (ábra. 16,4), majd plastinaAvyzhimaet olaj a lemez 27. Az a lapok felületének közvetlen kapcsolatba. Ebben az esetben fél-folyadék-csont súrlódás jön létre.
Elegendően magas skorostiVA (ábra. 16,4, B) plastinaApodnimaetsya az olaj réteget és vesz ferde helyzetben, ahogy az emelkedés gyalulás vagy vízisí, azonban zyaschie-víz.
Az olajjal töltött lemezek között szűkülő rés alakul ki, és a mozgás folyékony súrlódási körülmények között történik. A folyékony súrlódási rendszerre való átmenet bizonyos sebességgel történik, amelyet V ^ kritikus sebességnek neveznek. Tekintsük a jelenség fizikáját.
„Az alapító ez az elmélet NP Petrov (1883). Később ezt az elméletet dolgoztak ki a műveit O. Reynolds, NE Zsukovszkij, SA fejezet-Lygina, Sommerfeld, A. Michel és számos egyéb tudósok.
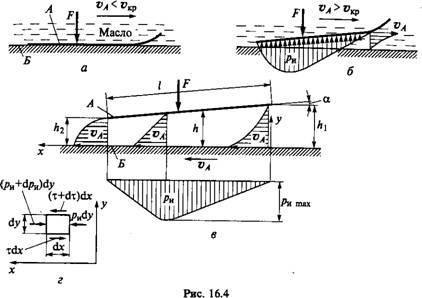
Az 1. ábrán. 16.4, b, a folyadékréteg egyik szakaszában a résen, a folyadéksebességek diagramját ábrázoltuk. A határréteg sebessége annyi pontot sebességeket valamennyi köztes pontot plastinAiB.Vo sebesség kisebb skorostiVAplastinyA. PlateAnabe-gaet folyadékkal és meghajtja a szűkítő résen keresztül. Ez a folyamat még tisztább lesz, ha figyelembe vesszük a lemezek fordított mozgását. Ehhez, legyen az egész rendszer visszafelé mozgás skorostyuVA.Interesuyuschee velünk relatív mozgását a lemezek nem fog változni, hanem plastinaAostanovitsya fordított mozgás, és mozgassa a plastinaBbudet skorostyuVAv ob ellentétes irányba (ábra. 16,4 a). A fordított elmozdulás sebességi diagramjait az 1. ábra mutatja. 16.4, több keresztmetszet. Ezeknek a diagramoknak a formája a jövőben a megfelelő egyenletek segítségével indokolható. Itt a sebességek irányában világos, hogy a folyadékot az A lemez alatt nyomják és a résen keresztül folyik.
Továbbá azt feltételezzük, hogy a lemez szélessége lényegesen nagyobb, mint a hossza / és a határban végtelen. Ez lehetővé teszi a folyadék oldalirányú áramlásának elhanyagolását a résen belül, és a bonyolultabb térbeli problémát a tengelyekhez és y-khez egy síkra csökkenti, a számunkra érdekes jelenség fizikáját tartva.
Az alapvető a Newton törvénye
Ahol m a folyadékrétegek nyírása során a belső súrlódás nyírófeszültsége, Fi a folyadék dinamikus viszkozitása, Pa • s, V az áramlás sebessége, m / s.
A Newton-törvény axiómának tekinthető, mint a mechanika első és második törvénye. A törvény fizikai jelentése az alábbiak szerint magyarázható. Két vékony szomszédos rétegnek van egy bizonyos sebességbeli különbsége. A rétegek közös határán egy eltolódás történik. A nyírási ellenállás arányos a keresztirányú sebességváltozás sebességével vagy a dv / dy származékkal. A p arányossági tényezője függ a folyadék tulajdonságaitól, és kísérletileg meghatározva van. E törvény alkalmazásával megtalálható a folyadékáramlás minden egyéb jellemzője.
Differenciáljuk a Newton-egyenletet
A szubsztitúció után a hidrodinamika alapvető egyenletét kapjuk egy folyadék egyenletes kétdimenziós áramlásához
Ahol h az olajréteg jelenlegi rétegvastagsága a résben.
A lemezenkénti szélességi térfogatáram a következő:
A folyadékáram folyamatosságának feltételei mellett a Q mennyisége nem függhet x -től (a rés Q minden szakaszában állandó). Az (16.4) egyenletből következik, hogy a nyomás gradiensét a réteg vastagságának változtatásával kell változtatni, összhangban a
A (16.4) és a (16.5) egyenleteket egyszerűsíthetjük, szem előtt tartva, hogy a lemez kilépése esetén, ahol A = A2s, a túlnyomás = 0. Mivel a (16.5) állandó tényező nem egyenlő nullával, az egyenletet a göndör zárójelben az A = A2 értékkel nullázzuk és megkapjuk
A (16.6) egyenletet (16.5) helyettesítjük és megtaláljuk
Ez az olajnyomás a hézagban, és egyensúlyba hozza az F külső terhelést, és a lemez mozgása folyadék súrlódás közben történik. Az egyenlet (16.7) lehetővé teszi számunkra, hogy egy nyomásgrafikont hozzunk létre (16.4, c ábra). A maximális nyomás a rés keskeny oldalára tolódik.
A kapott megoldások segítségével az alábbi következtetéseket vonhatjuk le.
1. Mivel a folyadékok áramlási sebessége megegyezik a szűkítő rés minden szakaszában, az átlagos áramlási sebességnek jobbra-balra kell növekednie (16.4. Ugyanakkor a lemezek határainál a folyadéksebességek állandóak és egyenlőek a lemez sebességével. Keresztmetszetben egybeesik a maximális nyomás, dpjdx = -G = 0.Pri e, egyenlet szerint (16,3), ez a szakasz skorostvv etsya változást lineárisan arányában. Most már könnyű megérteni, hogy azzal a feltétellel, hogy növeli a átlagsebessége a jobb oldalon Nala, a diagram secheniiHbudet homorú, és a D2 rész - domború. A rétegek bármely szakaszában és bármelyik szakaszában a sebességek a (6.3) egyenletből számíthatók.
2. Megállapítjuk a nyomás függését az olajréteg vastagságára. A középső szakaszban A = (AI + A2) / 2. Ebben az esetben a (16.7) helyettesítése után megkapjuk
Figyelembe véve a rések kis értékét (néhány mikron) és az a szöget, feltételezzük, hogy áthaladó d2 = 0 [6]. majd
Ennek következtében a nyomás fordítottan arányos az olajréteg vastagságával. A csapágyaknál ez a vastagsága tíz és egy század milliméteres, ezért a nyomás nagyon nagy értékeket érhet el.
3. Ha a dőlésszög plastinyAstremitsya nullára, akkor a határérték budeth = h = h2i egyenletben (16,7) megkapjuk /? U (00) / 0 = = 0. Ebből következik a fontos következtetés, hogy az egyik a feltételek kialakulását A folyékony súrlódás módja egy szűkülő rés jelenléte, amelyet általában kli-new néven neveznek.
Példánkban az íves rés kialakítása az A lemez peremezett peremével történik. Ha a csapágyszerkezet nem rendelkezik ékkel, akkor a folyadék súrlódása nem alakulhat ki a csapágyban. Például egy egyszerű lapos csapágy (lásd a 16.1., B. Ábrát) nem rendelkezik ékeltakarással, és nem tud folyadékcsont súrlódással dolgozni. Az éknyílás és következésképpen a csapágycsapágy csapágyfelületének folyékony súrlódási körülményeinek kialakítása érdekében különleges alakot kapnak (lásd a 16.11. Ábrát).
Sugárcsapágyaknál a rés ék alakja magában az alváz szerkezetében rejlik. A tengely és a bélés lapjainak elmozdulása következtében alakul ki (Fig.16.S, a).
A w> Q szögsebességnél a kardántengely felemelkedik az olajban, és kissé elmozdul a forgásirányban az 1. ábrán jelzett pályán. 16,5, b. Az 1. ábrán. 16.5, a, b: 1 - az ékhézag, 2 - a csap középpontjának útja növekvő fordulatszámmal; 3 - nyomásdiagram az olajrétegben, 4 soros központok. A növekvő szögsebességgel a szétválasztó olajréteg vastagsága nő, és a nyereg középső része megközelíti a bélés közepét. A központok közötti távolság egybeesik a teljes értékkel
A Niya központok nem lehetnek, mert ez megszakítja a rés ék alakját, mint a folyadék-súrlódási rendszer egyik feltétele.
A vizsgálatok azt mutatják, hogy bizonyos geometriai paraméterekkel rendelkező csapágyaknál az olajréteg vastagsága a csapágy működési módjának