Dinamikus adatszerkezetek
Dinamikus memóriaelosztás
A p = select (N) függvény egy mutatót visz vissza az N hosszúságú memóriaterületre,
C, p = új (N) (egy határozatlan mutatótípus).
1) A mutató beírása.
Szigorú gépelési nyelveken az int * p és a char * g nem egyenértékű => típus konverzióra van szükség.
2) Engedje el az elkülönített memóriát
· Explicit mechanizmus (programozó) - elpusztítani (p);
· Nincsenek kifejezett mechanizmusok (OS) - megsemmisül, ha nincs hivatkozás az objektumra, lehetséges az időzítésen keresztül végrehajtani, programok befejezése után túlcsordulás esetén.
3) Az akasztás problémája (amikor egy dinamikus objektum egy másik dinamikus objektumra utal)
A memóriában vannak tárgyak, amelyeknek nincs referenciája. Ennek az objektumnak a megsemmisítésével elveszítheti a referenciáit az összes al-objektumára.
4) A lógó mutatók problémája (a megrongálódott tárgyakra való hivatkozások továbbra is fennmaradnak);
5) Memória fragmentálása
Destroy p3 és p5 - az új objektum elég memóriával rendelkezik, de nem lesz egyetlen
A dinamikus memóriával való munkavégzés szabályai kifejezett megsemmisítési mechanizmusok esetén:
1) Ne engedje meg a lógó tárgyak jelenlétét. Ehhez először el kell pusztítania az összes csatolt objektumot.
2) Ne hagyja a lógó kapcsolatokat, azaz az objektum megsemmisítése után törölje és hivatkozzon rá - p = NULL.
3) A fragmentáció minimalizálása. Ehhez el kell pusztítani az objektumokat a létrehozásuk fordított sorrendjében: p5 - p4 - p3.
A dinamikus memória mechanizmus végrehajtása C:
1) Dinamikus memória kiosztása a void * malloc (size_t size) függvény segítségével.
Például ha 10 tömb elemre van szüksége, akkor:
A szükséges size_t méret nagyobb lehet, mint a szükséges (az igazításhoz)
2) A function void * calloc (méret_t szám, méret_t méret);
a fogadott memória összes értéke nulla.
3) üres szabad (üres * p)
a mutató az előzőleg rögzített memóriablokkra mutat a műveletekkel malloc, calloc, realloc, azaz a szabadítandó bájtok száma = a rögzítés során kapott bájtok száma
konvertálja az int-et a szabad ((void *) A) érvénytelenítéséhez;
4) A function void * realloc (void * p, méret_t új méret)
Megváltoztatja a korábban rögzített memória blokk méretét, p - a mutató a blokk elejére, a méret méretét bájtban. A blokk áthelyezhető a memóriába, ha a méret megváltozik.
Fák. FOGALOMMEGHATÁROZÁSOK, OSZTÁLYOZÁS, MUTATÓ MÓDSZEREK.
A T alaptípusú fa:
1) Vagy egy üres fa
2) Vagy a T típusú csúcs véges számú társult fával, T típusú alapokkal (alsókkal).
(Egy csúcspont által hivatkozott fa - egy rész)
A csúcs, amelyre a másik csúcs közvetlenül hivatkozik, az leszármazottja. A fordított csúcs az őse.
A csúcs, amely nem lesz leszármazotta, egy fa levele.
Ha a csúcsokat számoljuk úgy, hogy minden egyes következő gyermek egy szinttel magasabb, akkor a 0-os csúcs a fa gyökere.
A csúcs, amely nem levél, belső csúcspontja.
Minden csúcs szintje a mélység (magasság). és maga a fa mélysége a csúcsok maximális mélysége.
A csúcsok azonnali leszármazottjainak számát egy adott csúcs fokának nevezik, a fák mértéke az összes lehetséges fok maximális.
Az ágak (szélek) száma, amelyeknek a gyökérről az x csúcsra kell haladni, úgy nevezzük, hogy az elérési út hossza x-re (a gyökérnek 0-as útvonala van).
Az egész fa útvonala (a belső útvonal hossza) az útvonal hosszainak összege az összes csúcsához.
Az átlagos útvonalhosszat a következő képlet határozza meg:.
A fát rendelésnek nevezik. ha minden csúcsból származó fióktelep is megrendelt.
A második fokú rendezett fák bináris fáknak nevezhetők.
Az n-edik (nagyobb, mint 2) fát nevezzük erősen elágazónak.
A minimális magasságú fákat tökéletesen kiegyensúlyozottnak nevezik (a csúcsok száma a bal és a jobb alsó rétegben legfeljebb 1 lehet - az összes csúcs feltételét).
Az ilyen rekurzív struktúrák kifejezésére hivatkozásokra van szükség.
Számos különböző módon lehet megjeleníteni a fákat (például egy bináris fa):
1) A bináris fák listájának ábrázolása a fa csomópontjainak megfelelő elemeken alapul. Minden elemnek van egy adatmezője és két mutató meze. Egy mutató segítségével az elemet a jobb gyermekhez lehet kapcsolni, a másik pedig balra. A levelek üres mutatói vannak a leszármazottaknak. Ezzel a fa ábrázolásával mindig mutasson egy mutatót a csomópontnak, amely a fa gyökere.
Megfigyelhető, hogy a reprezentációnak ez a formája hasonló az egyszerű lineáris listákhoz. És ez a hasonlóság nem véletlen. Valójában a bináris fa ábrázolásának módja egyfajta multisesszió, amelyet egy sor lineáris listák kombinációja alkot. Minden egyes lineáris lista kombinálja azokat a csomópontokat, amelyek az ösvényt a fa gyökerétől az egyik levelig belépték.
struct binary_tree * left;
struct binary_tree * right;
Ezután az üres fa egyszerűen úgy határozható meg, hogy a Root változót nullára állítja:
Root = NULL;
2) A tömb formájában a teljes bináris fa legegyszerűbben ábrázolható, mivel minden szinten szigorúan meghatározott számú csúcsot tartalmaz. A csúcsok egymás után balról jobbra számozhatók a szintek szerint, és ezeket a számokat indexként egydimenziós tömbben használhatjuk.
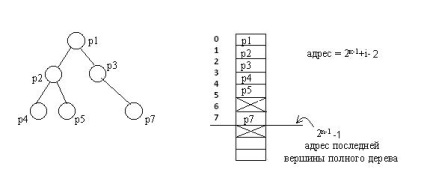
Ha a fa szintjeinek száma nem változik jelentősen a feldolgozás során, akkor egy teljes bináris fa reprezentálása ezáltal sokkal gazdaságosabb lesz, mint bármelyik listák szerkezete.
A bináris fa reprezentált módjának fő hátránya, hogy az adatszerkezet statikus. A tömb méretét a bináris fák maximális lehetséges szintje alapján határozzák meg. És annál kevésbé teljes a fa, annál kevésbé racionálisan használják a memóriát.
BINÁRIS FÓLIA, MŰVELETEK.
Bináris fa - egy véges halmaza (csomópontok), amely üres vagy egy gyökér két különálló bináris részfák nevezzük balra és jobbra részfáját a gyökér.
A minimális magasságú n csúcsokkal rendelkező bináris fa létrehozásához a következő szabályokat kell használni:
0) Ha n = 0, akkor a vég;
1) Építsd fel a csúcsot
2) Hozzon létre egy bal oldali foltot csúcsokkal;
3) Hozzon létre egy jobb oldali szubtétet csúcsokkal.
Műveletek bináris fákkal:
· Prefix bypass - csúcs, bal, jobb (+ ab):
prefix_walk (struct binary_tree * t)
· Infix bypass - bal, csúcs, jobb (a + b);
· Postfix - bal, jobb, csúcs (ab +);
Az adatelemek egy egyedi kulcs értékének keresésekor bináris keresési fákat használnak a keresési fában - a jobb oldali> x (csúcs) alatti összes csúcs, a bal oldali szubtree összes csúcsa N elemeket lehet szervezni egy bináris fához, amelynek magassága nem nagyobb, mint a log2 (N). ezért N elemek között keresni, nem feltétlenül több mint log2 (N) összehasonlítást igényel, ha a fa tökéletesen kiegyensúlyozott. Ebből következik, hogy egy fa megfelelőbb struktúra a keresés megszervezéséhez, mint például egy lineáris lista.Kapcsolódó cikkek