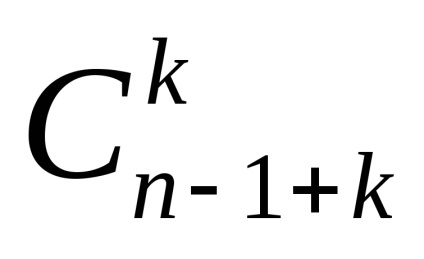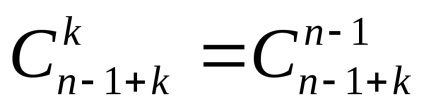Az urna séma a választás nélküli választás, figyelembe véve a megrendelést
2. tétel. Az in n elemek kiválasztási sémájában szereplő minták teljes száma a visszatérés és a sorrend figyelembevétele nélkül az alábbi képlet
és az elemek cellákhoz való hozzárendelésének számát nevezzük.
Bizonyítás. Az első labdát úgy lehet választani, ahogyan. Ezekkel a módszerekkel a második gömböt n-1 módon lehet kiválasztani stb. Az utolsó k-es gömböt úgy lehet megválasztani (n-k + 1). Tétel 1. a választék összes száma
amit be kellett bizonyítani.
Következmény 1. Az n elemek lehetséges permutációinak száma n!
D
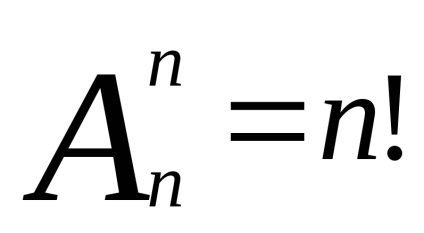
Az urna séma: választás visszaadás nélkül és a megrendelés figyelembe vétele nélkül
Tétel 3. Az elemek kiválasztási sémájának összes száma az n-ból származó elemekből a visszaadás nélkül és a megrendelés figyelembe vétele nélkül
és
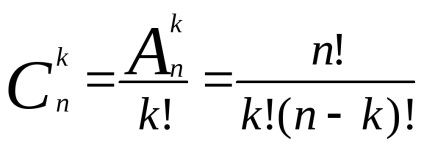
Bizonyítás. Megjegyezzük, hogy a 1. Következtetés szerint. Egy adott összetételből (k elemekből álló) minden egyes mintából k! választások, amelyek csak az elemek sorrendjében különböznek egymástól.
Ez azt jelenti, hogy a minták száma rendben és k-ben különbözik! több mint a minták számát, amelyek csak összetételben különböznek egymástól. választóvonal
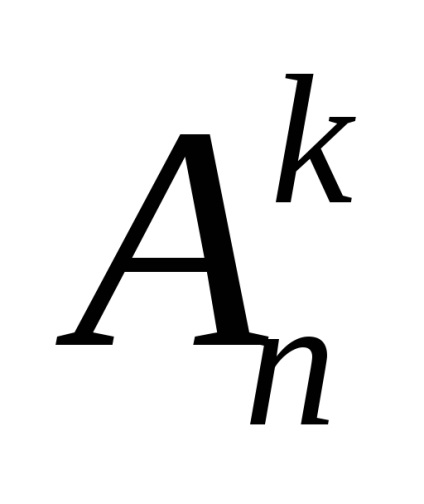
Az urna rendszer: választás visszatérítéssel és a megrendelés figyelembevételével
T
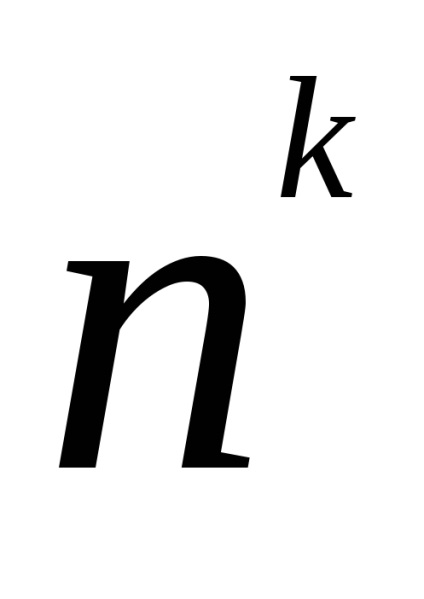
Bizonyítás. Az első labdát úgy lehet választani, ahogyan. Mindegyik módszerrel a második labdát lehet fogadni vendégfogadó utaknak és sokszor.
Urn séma: választás visszatéréssel és megrendelés nélkül
Vegyünk egy urnát két golyóval, és sorolja fel az eredményt, amikor kiválasztunk két golyót az urnából, amikor kiválasztunk egy visszatérést:
Figyelembe véve a rendelést
Megjegyezzük, hogy a "megrendelés figyelembevétele nélkül" rendszerben 3 különböző eredményt kaptak, ellentétben a "figyelembe véve a megrendelés" rendszertől. (a 4. szám és a 4. tétel szerint); és hogy a "permutációk számát" nem lehet megosztani, akkor a 4-es szám 3-as lesz megszerezve.
T
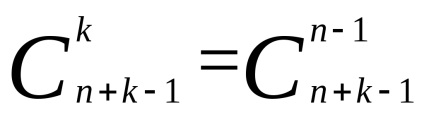
Bizonyítás. Vizsgáljuk meg részletesen, hogy az ilyen kiválasztási rendszer két különböző eredménye különbözik-e egymástól. Nem törődünk a számok sorrendjével, vagyis csak azt vesszük figyelembe, hogy hányszor gyűjtötték össze a golyószámok gyűjteményét az 1. golyó, a 2. golyó, ... gyöngy szám. Vagyis a választás eredményét a k1, k2, ... k számok halmaza képviseli. ahol k az I. golyó előfordulásainak száma a mintában, és k1 + k2 + ... + kn = k. Ebben az esetben a kísérlet két eredményei eltérőek, ha a megfelelő k1, k2, ..., kn értékek nem esnek egybe.
Képzeljen el egy másik kísérletet, amely pontosan ugyanolyan eredményekkel jár (és ennek következtében vannak olyanok is). Vannak n dobozok, amelyekben a golyókat elhelyezik. Csak a labdák számát érdekli az egyes dobozokban. Vagyis a kísérlet eredménye ismét a k1, k2, ... k számok halmaza. ahol ki a golyók száma az i számmal. és k1 + k2 + ... + kn = k. A számok még mindig természetes értékeket vesznek fel, vagy egyenlő 0.
Most ábrázoljuk az ilyen elhelyezés eredményét olyan rendszer formájában, amelyben a függőleges vonalak a dobozok közötti partíciókat jelölik, és a körök a dobozok golyói:
A 9 golyó 7 dobozba helyezésének eredményét látjuk. Ott 1. doboz 3 golyót tartalmaz, a 2. és a 6. ládák üresek, 3. 1 doboz tartalmaz egy labdát, és a 4. és 5. dobozok 2 golyós. Egy labdát áthelyezünk az első dobozról a másikra, és az elhelyezésnek egy másik eredményét is ugyanúgy képviseljük:
Látjuk, hogy az összes szállás nyerhető megváltoztassák egymás labdák és falak, vagy a labda rasstavlyayak nan-1 + k helyére. Kiszlon-1 + k a következőképpen állítjuk elő: yn fiókok van rovnon + 1 partíció, figyelembe véve a szélsőséges, vagy n-1 partíciót, kivéve a szélsőséges, aki nem lehet mozgatni. És vannak k golyók. Után megy keresztül, minden lehetséges módon rasstavitk golyó etihn-1 + k helyszínek (rakjuk a maradék partíció hely), végiglépdelni szükséges szállást.
De az n-1 + k-k golyóinak rendezésének módja pontosan megtörténik