A Gauss-tétel és a b vektor forgalmi tétele
A mágneses indukció vektorának bármilyen zárt felületen való fluxusa nulla értékű:
Ez a tétel tükrözi azt a tényt, hogy nincsenek mágneses töltetek, aminek következtében a mágneses indukciós vonalaknak sem eleje, sem végük nincsenek zárva.
Így a B és E vektorok áramlása zárt felületen keresztül különféle kifejezéseket kapunk az örvényben és a potenciális mezőkben.
Példaként kiszámítjuk a B vektor fluxusát mágnestekén keresztül. Egy mágneses indukció egy mágneses permeabilitású maggal rendelkező mágnesszelepen belül m. a (119.2) szerint egyenlő B = # 956; 0 # 956, NI / l
Az S terület mágnesszelepének egyik tekercsén keresztül mágneses fluxus egyenlő: Ф1 = BS
és a teljes mágneses fluxus, amely a szolenoid összes tekercsével van összekötve, és amelyet fluxkötésnek neveznek,
Az elektrosztatikus mező intenzitásának vektorának keresztezéséhez hasonlóan a mágneses indukció vektorának keringése kerül bevezetésre. A B vektor keringése egy adott zárt körvonal mentén az integrál
,
ahol dl - egységnyi hossza a kontúr vektor mentén irányul megkerülő áramkör, Bl = B cosa - A a vektor komponense irányába érintő a kontúr (tekintve kiválasztott irányba), egy - közötti szög B és dl.
teljes áram törvény a mágneses mező vákuumban (tétele Circulation vektor B): A cirkulációs a vektor egy tetszőleges zárt pálya egyenlő a terméket a mágneses állandó m0, hogy az algebrai összege áramok által lefedett CON-túra:
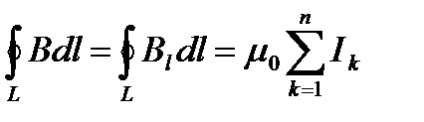
ahol n a tetszőleges alakú L kontúr által lefedett áramok száma. Minden áramot annyiszor számolnak, amennyit az áramkör fedez. Pozitív pozitív áramot tekintünk pozitívnak, amelynek iránya egy jobb csavaros rendszert képez a kontúr irányának irányával; az ellenkező irányú áramot negatívnak tekintjük.
Az E és B vektorok forgalmának kifejeződéseinek összehasonlításával látjuk, hogy alapvető különbség van közöttük. Az elektrosztatikus mező E vektorának keringése mindig nulla, vagyis az elektrosztatikus mező potenciál. A mágneses tér B vektorának keringése nem nulla. Az ilyen mezőt örvény mezőnek nevezik.
Tétele Circulation a vektor a tanulmány a mágneses mező ugyanolyan értékű, mint a Gauss-tétel az elektrosztatika, mivel lehetővé teszi, hogy megtalálja a mágneses mező indukció alkalmazása nélkül Biot - Laplace Savara-.
A mágneses indukció sorai folyamatosak: nincsenek sem kezdetük, sem végük. Ez a helyzet minden áramkör által okozott bármely mágneses mezőre. A folyamatos vonalakkal rendelkező vektor mezőket vortex mezőnek nevezik. Látjuk, hogy a mágneses mező egy örvény mező. Ez a lényeges különbség a mágneses mező és az elektrosztatikus mező között.
Az elektrosztatikus mezőben a feszültségvonalak mindig nyitottak: elektromos töltéssel kezdődnek és végződnek. A mágneses mező indukciós vonalai nem kezdődnek, sem véget nem érnek. Ez megfelel annak a ténynek, hogy a természetben nincs mágneses töltés.
Az elektromos töltések mozgása elektromos áram. Mivel nincs mágneses töltés, nincs mágneses áram.