A fém elméleti és valós ereje

előző ◈ a következő

A kristály erősségének elméleti számítását először J. Frenkel végezte. Ennek alapja két sor atom egyszerű modellje volt, amelyek az érintőleges stressz m hatására (5.1. Ábra) egymáshoz képest eltolódnak. Feltételezték, hogy a felső sor atomjai az alsóhoz képest egy, egyidejűleg mozognak. Ezt a mechanizmust általában nyírószerkezetnek nevezik.

Az 1. ábrán. 5.1. Az interplanáris távolság (a sorok közötti távolság) egyenlő a, és a csúszási irányú atomok közötti távolság b. Az intézkedés alapján nyírófeszültség x atomi sorok vannak tolva egymáshoz képest, beleesik az egyensúlyi helyzet az ilyen pontot, mint az A és B, ahol a nyírófeszültség fenntartásához szükséges ez a konfiguráció nulla. Ez a feszültség nulla, és abban az esetben is, ha mindkét sorban atomok található pontosan egymásra pozícióban a C és D A köztes helyzetekben feszültség van valamilyen véges értékek, amelyeket periodikusan változtatjuk a képernyőn rács. Ha a nyírófeszültség hatására az elmozdulás x, akkor a feszültség periodikus függvénye lesz a x b idõszakkal. A legegyszerűbb formában ezt a függést szinuszos görbeként lehet ábrázolni (lásd az 5.1. Ábrát):
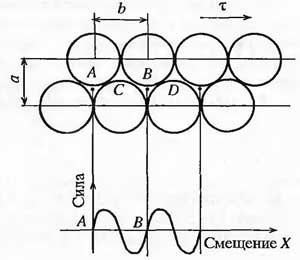
x = ksm (2nx / b). (5.1)

Kis elmozdulások esetén x = klnx / b. A Hooke-törvény alkalmazásával a nyírófeszültség nagysága más formában ábrázolható: m = Gx / a, ahol G a nyírási modulus; x / a a nyírási deformáció.
Ha a fenti kifejezéseket az x-vel azonosítjuk, akkor; x = Gb / lmi; Ha ezt az értéket helyettesíti (5.1), akkor a következőket kapjuk:
x = ksin (2nx / b)

Ha feltételezzük, hogy a = b, akkor az elméleti kritikus nyírófeszültség megközelítőleg egyenlő G / 2n értékkel. Például a réz kristályok G = 46 LLC MPa, ezért az elméleti érték m = 7320 MPa. Ugyanakkor a valós rézkristályok esetében a megfigyelt nyírási ellenállás csak 1,0 MPa. Így az erő elméleti értéke több nagyságrenddel magasabb, mint a tényleges érték.

Finomítás A fenti számítás segítségével közelebb a valósághoz a periodikus törvény attól függően változik, t x expressziójához vezet a TCR = G / 30 (számítási McKenzie), amely szintén meghaladja több nagyságrenddel valós nyírási ellenállás.

Hasonló érveket lehet abban az esetben, ha eredményeként a rendes stressz akkor egyidejű szünet interatomi kötvények két sorban az atomok és a crack. A megsemmisítésre fordított munkát két új felület létrehozására fordítják, amelyek éves felszíni energiával rendelkeznek. Az ideális kristály elméleti ereje, amelyet két sor atom leválásának egyenlőségének és a repedésben keletkező felszíni energiának az egyenlőtlensége állapota határoz meg.

Az anyagok tényleges szilárdsága több nagyságrenddel kisebb, mint az elméleti szilárdság. Magyarázat a különbségek elméleti és a tényleges anyagszilárdság lehetővé teszi, az elmélet a kristályszerkezet hibák, lehetővé tette, hogy felfedje a lényege a jelenségek során képlékeny alakváltozás, és állítsa be a fizikai természetét a képlékenységet és erejét fémek és ötvözeteik.

Kapcsolódó cikkek

előző ◈ a következő