Trigonometrikus szintezés
Trigonometrikus szintező - meghatározásának módszere a különbség a magasságtól pont a Föld felszínén a mért szög és a hossza a ferde rálátás vagy vetülete a vízszintes síkban.
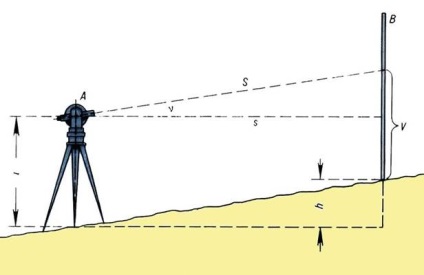
5. ábra - Trigonometrikus szintezés
V - a látás magassága;
h- magasságkülönbség (felesleg) az A és B pontok között;
S-látóvonal; s - a látómező vízszintes vetülete;
n a látótávolság dőlésszöge.
A h (5. ábra) túllépését a következő képletek határozzák meg:
h = s * tg # 957; + i - V vagy
h = S * sin # 957; + i - V,
ahol # 957; - a látótávolság dőlésszöge;
S - a látómező hossza;
s - vízszintes vetület;
i - a készülék magassága;
V a látás magassága.
Trigonometrikus kiegyenlítést alkalmaznak a topo-geodéziai munkák a föld felszínén és felmérési felméréseket a bányászati munkákban, amelyek lejtései több mint 8 °.
A trigonometrikus szintezést geodetikusnak vagy szintezőnek nevezik ferde sugárral. Ezt a teodolit végzi; A két pont közötti többlet meghatározásához meg kell mérni a lejtést és a távolságot. A pont teodolit szerelt, a B pontban - vasúti vagy mérföldkő ismert magassága V. szögmérés teodolittal teleszkóp, amikor mutatva, amely a felső pólus vagy vasúton (ábra6 4,38). Az LK szegmens hossza az LC és CK szegmensek összegeként, az LB és a BK szegmensek összegeként jeleníthető meg. Az LC szegmens megtalálható # 916; JLC: LC = S * tg # 957; A többi szegmens az ábrán látható.
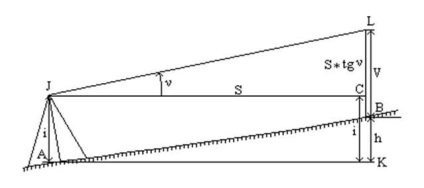
Fig.6 4.38 - A távcső teleszkópjának dőlésszögének mérése
LC + CK = LB + BK és S * tg ( # 957;) + i = V + h.
Ezért kifejezzük a h felesleget
A trigonometriai kiegyenlítés képletét a Föld görbülete és a refrakció figyelembevételével derítjük le. Miatt fénytörés a fénysugár a felső végén mérföldkövek a görbe és észlelési csővezeték lesz irányítva mentén érintő e görbe azon a ponton, J. céielektródacső vonal metszi mérföldkövek folytatjuk L1, ahelyett, L. felhívni szintű felületek A, B, J (7. ábra, 4.39).
Tegyen egy vonalat a sík felületre a J ponton, és jelezze: a készülék magassága - i. a mérföldkő magassága V, az AB vonal vízszintes vonala S.
Az A ponthoz viszonyított A fölötti értéket a BK szegmens fejezi ki. Az L1K szegmens az 1. ábrán látható. 7 4.39 - Trigonometrikus szintezés a Föld görbületét figyelembe véve és a refrakció kétféle módon fejezhető ki részei révén:
L1K = L1E + EF + FK,
L1K = L1L + LB + BK.
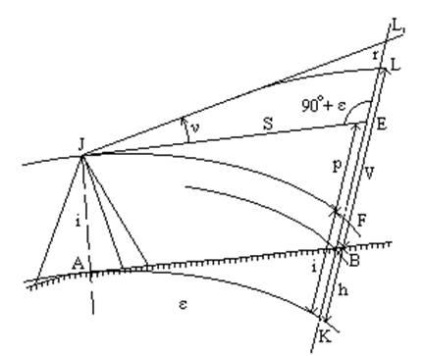
Ábra. 7 4.39 - Trigonometrikus kiegyenlítés figyelembe véve a Föld görbületét és fénytörését
Az L1E szegmens megtalálható # 916; JL1E. Ez a háromszög négyszögletesnek tekinthető, mivel az L1EJ szög nagyon kis mértékben különbözik az egyenes vonaltól, csak a központi szög értéke # 949; = (S / R) * r. Ez a szög S = 1 km-en nem haladja meg a 0,5 '-ot.
De mivel JE = S, akkor L1E = S * tg (# 957;).
Az EF szegmens kifejezi a Föld görbületének hatását:
Az FK szegmens megegyezik az eszköz FK = i magasságával; az L1L szegmens a fénytörés hatását fejezi ki:
L1L = r * (S2 / 2 * R) * k = p * k;
az LB szegmens egyenlő a mérföldkő V. magasságával.
h = S * tg (# 957;) + (i-V) + (p-r),
h = S * tg (# 957;) + (i - V) + f. (8 4,68)
A távolság mérése menetes távolságmérővel a felesleges formula kissé megváltozik; mivel S = (Cl + c) * Cos2 (# 957;), akkor
h = 0,5 * (Cl + c) * Sin (2 * # 957;) + i - V + f = h '+ i - V + f,
A h '= 0,5 * (Cl + c) * Sin (2 * # 957;) tacheometrikus feleslegnek nevezzük.
S = 100 m-nél az f értéke elhanyagolható, mivel f = 0,66 mm.
S2. ahol S a távolság (több száz méter).
A trigonometrikus szintezés feleslegének méréséből adódó hiba becslések szerint 2 cm és 10 cm között van 100 m távolságonként.
A túlkínálatok egymást követő mérésével egy nagy magasságú tanfolyamot kapunk; tengerszint feletti magasságban a dőlésszögek mértek kétszer: előre és hátra.
Ellenőrzési kérdések a hallgatók önkészítéséhez:
1. Mi és milyen módszereket határoz meg a szintezés során?
2. Milyen szintezést nevezünk geometrikusnak, milyen eszközöket hajt végre?
3. Hogyan oszlik meg a pontossági szintek, mit jelent a számjegy a készülék titkosításában?
4. Hogyan kell a szinteket megosztani a csővezeték látótengelyének vízszintes pozícióba helyezésének módjával?
5. Mi a név és cél a speciális csavarok szintjei hengeres szinten?
6. Mi kompenzálja a szintkompenzátort?
7. Rajzolj a vízszintes tengelyek diagramját hengeres szintre.
8. Rajzolj a vízszintes tengelyek diagramját a kompenzátorral.
9. Milyen részleteket szolgáltatnak a beállító csavarokkal?
10. Hogyan történik a kalibrálás és a szint kerek szintjének beállítása?
11. Hogyan állíthatja be a vízszintes rúdat függőlegesen?
12. Formázza meg a szint fő geometriai állapotát.
13. Milyen módon ellenőrizték az elvégzett szint fő feltételeit?
14. Milyen beállítási csavarokat használnak a különböző típusok szintjén, ha a szint fő geometriai állapota nem teljesül?
15. Mit mutatnak a szintező mozgalomban kötőanyagok?
16. Miért és hol vannak a kiegyenlítő mozgásban a köztes pontok?
17. Miért van a szintezés az állomáson a nyakkendő pontok közepén?
18. Mekkora megengedhető maradék az 1 km hosszúságú technikai kiegyenlítés során?
19. Mit neveznek a műszerhorizontnak? Mire számít a képlet?
20. Mi a pontot a) meghaladó értékkel, b) a műszerhorizonttal?
21. Milyen és milyen eszközöket mértek a trigonometriai szintezés során?
22. Milyen formulával lehet kiszámítani a felesleges értéket a trigonometriai szintezéshez, ha azt egy elektronikus állomás segítségével végzik?
23. Mely képlet alapján lehet a trigonometrikus szintezést kiszámítani, ha a távolságot menetes tartománymérővel mérik?
24. Mi a készülék magassága? Hol van a jel a teodoliton vagy az elektronikus állomáson, amelyre ezt a magasságot mérik?
25. Hány és milyen elemeket kell trigonometrikus szintezéssel meghatározni a pontok közötti többlet kiszámításához? Erősítse meg a választ az áramkörrel.
Tesztelje a "Szintezés. Szintek »
1. Geometriai szintezés:
1) a magasságok meghatározása ferde sugárral;
2) a feleslegességek meghatározása a képzeletbeli sugárral;
3) a feleslegek vízszintes sugárral történő meghatározása;
4) a vonat tömegének meghatározása.
2. A műszerhorizont:
1) a rackre számítva, amely egy ismert védjeggyel ellátott ponton van;
2) a látótér magassága a referenciafelület felett;
3) jelölje meg azt a pontot, amelyen a rake telepítve van;
4) az eszközzel elérhető pontosság.
3. A geometriai szintezéssel a műszer horizontja megegyezik:
1) a hátsó és az elülső rúdra vonatkozó értékek összege;
2) a számítások különbsége a hátsó és az első sávokon;
3) a hátsó és az elülső pontok jelzéseinek fele;
4) az állványra történő számlálás mennyisége és azon pont jelölése, amelyen a rack telepítve van.
4. A geometriai szintezés eszközhorizontjának kiszámításához ismerni kell:
1) az állomásról kiugró pontok jelzése;
2) az előző állomás műszerének horizontja;
3) a vetített terület jelzése;
4) a pont jelét és a számlálást a racken, amelyen áll.
5. A geometriai kiegyenlítést eszközök végzik:
4) műholdvevő.
6. A geometriai szintezéshez használja: