A csavart érpárú szigetelés működőképességének és egyenértékű dielektromos permeabilitásának értékelése
Bibliográfiai leírás:
Az elsődleges és másodlagos átviteli paramétereket és a kommunikációs kábelek kölcsönös hatásainak paramétereit a vezetőközeg geometriai és elektromos paraméterei határozzák meg. Mivel nincs közös megoldások a probléma becslésére munkaképességét a kábel és az azzal egyenértékű permittivitását a közeg között a két vezető. A megoldás erre a problémára releváns a algoritmikus automatikus vezérlés paramétereit extrudáljuk porózus szigetelés bevezetésével körök kapcsolatot biztosító kompenzáló hatás dinamikus szabályozási hiba az egyik paraméter (átmérő vagy dielektromos izolálás permeabilitás) generalizált kábel minőségi paraméter (munkaképesség vagy impedancia) képezve perturbált folyamat a második paraméter automatikus stabilizációs hurokjában (dielektromos permittivitás vagy átmérő szigetelés) [1].
Tekintettel az adatátvitelre (LAN-kábel) vonatkozó rádiófrekvenciás kábelek alapját képező sodrott érpár elektromos paramétereinek meghatározására. Az 1. ábrán. Az 1. ábra egy árnyékolatlan csavart érpár keresztmetszetét mutatja, amely két magból áll, amelyek szigetelési átmérője eltér.
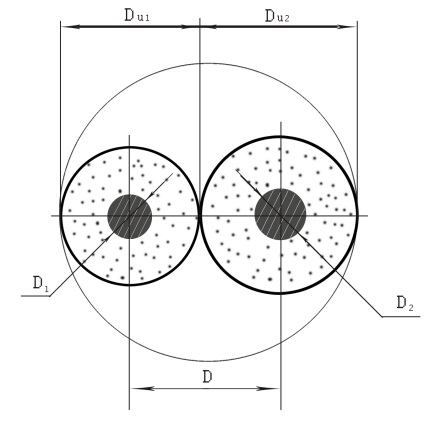
Ábra. 1. A LAN-kábel keresztmetszete
Hagyományosan a vezetőközeg ekvivalens permittivitását becslik mindkét mag súlyozott átlagszigetelési értékének, figyelembe véve keresztmetszeti területük arányát. Ezt a becslést alacsony pontosság jellemzi, ami elfogadhatatlan a nagy teljesítményű kábelek tervezésében és gyártásában. A munkaképesség becsléséhez hagyományosan megállnak a VN Kuleshov által kiváltott képlet [2], amelyet szintén alacsony pontosság jellemez. Ezt a problémát megoldjuk konformális átalakítással.
A láncon belüli folyamatokat meghatározó kezdeti kapcsolatok megszerzéséhez a lánc elsődleges paramétereit alkalmazzuk. Az R és L paramétereket az ekvivalens áramkörben (2. ábra) a Z = R + jωL lánc hosszanti ellenállása jellemzi. és a C és G paraméterek az Y = G + jωC lánc keresztirányú teljes vezetőképessége. ahol R a vonal vonalellenállása, L a lineáris induktivitás, C a lineáris vonal kapacitás, és G a szivárgási együttható.
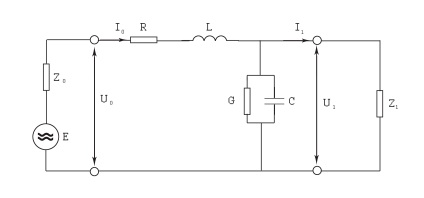
Ábra. 2. A kommunikációs vonal egyenértékű áramköre
Ha az érték a primer kör paraméterek változatlanok maradnak az egész hosszában, egy ilyen lánc nevezzük szabályos (egységes) [3]. Az aktív elektromágneses energia veszteséget való terjedése közben a lánc mentén miatt az elsődleges paraméterek R és G. első jellemzi a hőveszteség a vezetékek és egyéb fém alkatrészek az megvezető rendszer (képernyőn, héj, páncél), a második - a veszteségeket a szigetelés.
Tekintsünk egy homogén láncot az R, L, C, G primer paraméterekkel (2. A differenciálegyenletek olyan rendszere, amely meghatározza a feszültséget és áramot a lánc bármely pontján az x koordinátának függvényében. van formája [4]:
Ez a rendszer minden homogén lánccal kapcsolatban érvényes, függetlenül annak kialakításától. A tervváltozás csak az elsődleges és a másodlagos paraméterek változásához vezet, beleértve a hullámellenállást:
A LAN-kábelt veszteségmentes vonalként fogjuk figyelembe venni. Ez azt jelenti, hogy a szivárgást nulla (G = 0), vagyis azt feltételezzük, hogy a vezetékek közötti tér nem vezető. Ezenkívül elhanyagoljuk a vezetékek veszteségét, figyelembe véve, hogy ideális esetben vezetőképes (R = 0). Mivel az ideális vezetékeknél a belső induktivitás nulla, ebben az esetben az L vonal teljes induktivitása csökken Le külső induktivitásától. Ezekkel az egyszerűsítésekkel a (2) képlet a következő alakú:
A munkakapacitás meghatározásához a konformális transzformációt használjuk a frakcionális lineáris függvény alkalmazásával [5]:
ahol a, b, c, d állandók, ad-bc ≠ 0 esetén. A reláció (4) megoldása z-re vonatkoztatva. lineáris frakcionális transzformációt is kapunk:
A frakcionális lineáris transzformációnak az a tulajdonsága, hogy a z-síkban lévő bármelyik kör egy ω-síkban és hátul körbe kerül, miközben a vonal egy végtelen nagy sugarú körnek tekinthető.
A frakcionális-lineáris transzformációnak is fontos szerepe van a szimmetrikus pontok megőrzésében: minden z1 és z2 pontpárt átalakít. szimmetrikusan egy tetszőleges Cz körhöz képest az z síkban. egy pár ω1 és ω2 pontra. szimmetrikusan a Cz kör Cω-képére vonatkoztatva a ω [5] síkon.
A tulajdonságok használatával lineáris frakcionált átalakulása fenntartani a kerülete és megjeleníti a terület között a vezetékek LAN -Kábel (ábra. 3) egy koncentrikus gyűrű, amely egy egyszerű kétszeresen csatlakoztatott régióban.
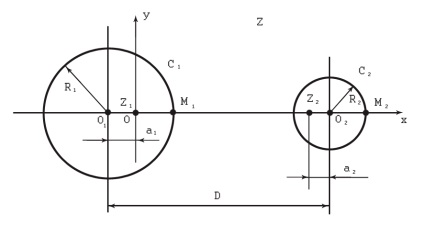
Ábra. 3. A LAN-kábelek Z-síkban történő összekapcsolása
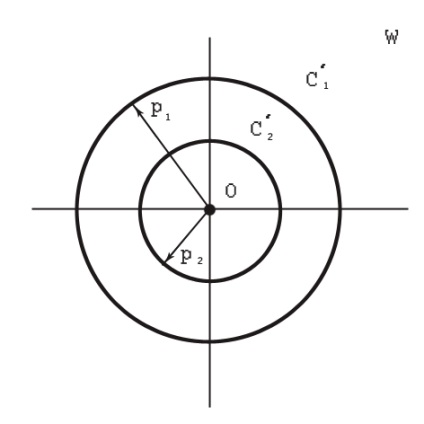
Ábra. 4. A LAN-kábelek összekapcsolása a W síkban
Ha megtaláljuk az z1 és z2 pontok pozícióját. egyszerre szimmetrikus mind a C1, mind a C2 körre vonatkozóan. amelyek egybeesnek az elektródák felületével, majd a térképezés alatt
A C1 és C2 körök a C'1 és a C'2 körökre lépnek. amelyre a ω1 = 0 és ω2 = ∞ pontok is szimmetrikusak lesznek. Ebből következik, hogy a C'1 és C'2 körök koncentrikusak, és középpontjuk egybeesik a ω sík eredetével. amely lehetővé teszi a LAN-kábel magjainak megmun- kálását a gömb alakú kondenzátor ismert formula szerint (4.
Most találunk szimmetrikus pontokat a C1 és C2 körök tekintetében. Az 1. ábrából. 3 van:
ahol a jelölés
Elhelyezés a Z1 szimmetrikus pontra. a C1 körön belül helyezkedik el. kapunk:
mivel könnyű látni ezt
következésképpen az ω függvény a következő alakú:
Figyelembe véve a konformális transzformációk változatlan kapacitásának megőrzésének tulajdonságát, az utóbbit az ω síkban találjuk párhuzamos kábeles magokra [5]:
kifejezés (12) a következő alakú:
Az ekvivalens εeq permittivitás meghatározásához ismét használjuk a konformális leképezést, de most az z-síkot (5. ábra) a t síkra (6. ábra) ábrázoljuk,
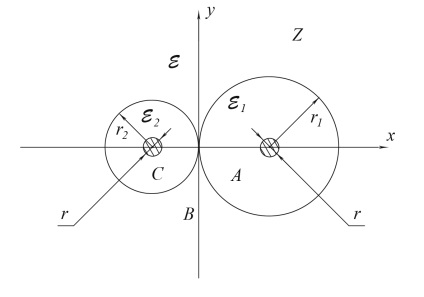
Ábra. 5. A LAN-kábelek összekapcsolása a Z-sík szigetelésével
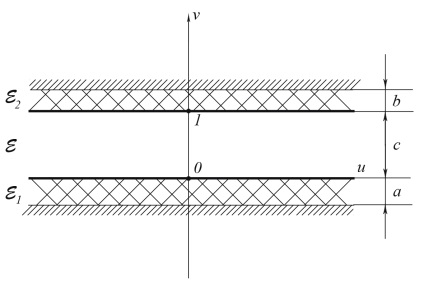
Ábra. 6. Az z-sík t-síkra történő leképezésének eredménye
Ehhez a feltérképezéshez a következő feltétel [5] szükséges:
Meghatározzuk u és v. figyelembe véve a (15), (16) és (17) kifejezéseket:
Miután megjelenítette a sík z-t a síkban t. egy lapos kondenzátort kaptunk végtelen lemezekkel. Ebben az esetben lehetséges meghatározni a dielektromos permittivitását. A két vezeték között a tápközeg ismeretlen egyenértékű dielektromos állandója lesz.
Ennek a problémának a megoldása érdekében az eredményül kapott kondenzátort három egymást követő kondenzált kondenzátorra osztják, homogén dielektrikumokkal a lemezük között, a megfelelő dielektromos permittivitással: ε1. e2. ε (7. ábra).
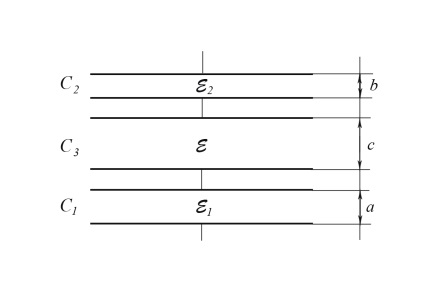
Ábra. 7. Egyenértékű áramkör három kondenzátor csatlakoztatására homogén dielektrikumokkal lemezek között
Az 1. ábrán látható. A 7-et a következő kifejezésből határozzuk meg:
A kondenzátorok paramétereinek a (19) kifejezéssel való helyettesítésével a következőket kapjuk:
A (20) bekezdésből az következik, hogy:
A kondenzátor kapacitását a következő képlet adja meg:
ahol l a lemezek közötti távolság:
A (21) kifejezésből be kell mutatni a m:
Figyelembe véve a (21) - (24) kifejezéseket, a következőket kapjuk:
Az a, b, c távolságok csak az a pontok koordinátáit határozzák meg a t síkra (6. ábra), amelyeknek a koordinátái a z-síkban vannak (5. ábra):
A (18) kifejezés segítségével ezeknek a pontoknak a koordinátáit kapjuk a t síkon:
A (24), (26) - (27) kifejezést a (25) kifejezésre helyettesítve, és figyelembe véve, hogy:
ahol Di és. D1 - a szigetelés átmérője, illetve a vezető d-átmérője, kapunk:
A (14) helyen helyettesítjük (28), és figyelembe véve, hogy:
Az Expression (29) egy árnyékolt csavart érpárú LAN-kábelre is érvényes, ha bevezeti a szűrési tényezőt és a csavar tényezőt.
Mirolyubov, NN Az elektrosztatikus mezők számításának módszerei. - M. Nauka, 1963.
Alapvető kifejezések (automatikusan generált). permittivitás, csavart érpár, munkaképesség, a permittivitás szigetelés egyenértékű permittivitás kör C1, C2 kerülete, a dielektromos állandója a közeg, a permeabilitás a szigetelés csavart, az elsődleges paraméterek, a sugara kör C2, az induktivitás hosszegységre átmérőinek a tömítéseket, a belső kerülete S1'opredelim, paraméterek sodrott egyenértékű permittivitású üzemi kábelkapacitás, elektromos jellemzőit az útmutató, csatlakozó kábel, munkaképesség.