Informatikai tanfolyam
Számok fordítása a decimális számrendszerről egy másik pozícióra
Mint már említettük, egy ember szokott dolgozni a decimális számrendszerben, és a számítógép egy bináris rendszer felé orientálódik. Ezért a humán kommunikáció a gépzel lehetetlen, anélkül, hogy egyszerű és megbízható algoritmusokat hozna létre számok fordítására egy rendszerről a másikra és fordítva. Szóval, hogyan alakítja át a számokat a tizedes rendszerről binárisra?
Tegyük fel, hogy a 11-es számot bináris számrendszerré kell átalakítanunk. Osszuk 11 2. 5 magánúton, majd a maradékot 1 Következésképpen a 11-es szám az utóbbi szám a bináris 1 Ahhoz, hogy megtalálja a második szakadék számokat találtunk különösen 5-2 újra kapjunk hányados és a maradék 2 1. Következésképpen a második számjegy a végétől a 11-es szám bináris ábrázolásánál szintén egyenlő 1. A 2. rész ismét osztva 2-el. A maradékban 1-et és 0-ot kapunk. A kapott 1 az első számjegy a 11 bináris számban. Az utolsó 0 részosztály fennmaradó része a második számjegy.
Ha egy nem egész számot - tizedes törtet szeretne konvertálni, akkor a következő műveleteket hajtjuk végre:
1. A szám teljes részét bináris rendszerré alakítjuk a fent leírt módon.
2. A törtrészet szorzással kell átszámítani a rendszer alapjába, amelybe a számot lefordítjuk.
A frakcionális rész - a 0,7-es szám a rendszer alapja - a 2-es szám szorzataként 1,4-et kapunk. Az adott szám teljes részét (1-es számjegy) kiválasztják, és a tört rész - a 0,4-es számot ismét 2-gyel meg kell szorozni.
Nyilvánvaló, hogy a 0.7 szám átvitelének folyamata határozatlan ideig folytatódhat. Sőt, hat lépésben megkaphatjuk a 0.101100 számot, és hét lépésben 0,1011001-et kapunk, ami pontosabb ábrázolása a 0,7-es számnak a bináris rendszerben. Az ilyen végtelen folyamatot bizonyos lépésekben lezárják, amikor úgy tekintik, hogy a szám reprezentációjának szükséges pontossága megvan. A fordítás eredményeképpen megkapjuk a választ:
A decimális számok más pozíciószámrendszerekre történő átszámításához ugyanazok a szabályok vonatkoznak, csak a rendszer alapja, amelyre a számokat le kell fordítani.


Számok fordítása a bináris számrendszerből a bináris és a backhez kapcsolódó rendszerekbe.
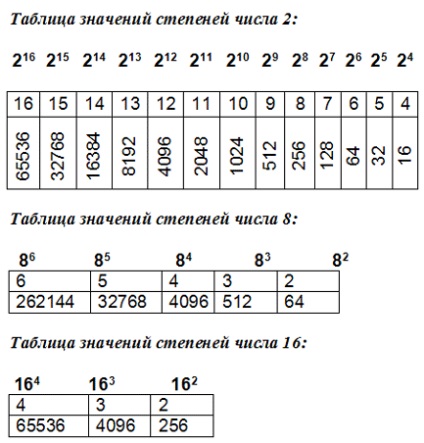
Nagy számok a bináris rendszerben nagyon nehézkes rekordok. Természetesen lefordíthatsz egy számot egy decimális rendszerbe, és írhatod ezt a formanyomtatványt, majd ha szükséges, fordítsd vissza, de mindezek a fordítások nagyon időigényesek. Segítséget nyújt a bináris - oktális és hexadecimális rendszerekhez. A kapcsolódó rendszerről a binárisra és a hátra történő fordítás azonnal elvégezhető az elmében.
A számrendszerek olyan kapcsolódó bináris rendszereknek tekintendők, amelyek alapja a 2-es szám teljesítményének értéke.
Például a kvaterner, oktális és hexadecimális jelölő rendszerek bináris rendszereket jelentenek.
A bináris rendszerből származó számok bináris rendszerhez történő konvertálásához a következő műveleteket kell végrehajtania:
1. Sorolja fel a számot egy sor számjegyre, amely egyenlő a rendszer alapja 2-es számának erejével, amelybe lefordítjuk.
2. Ha a felsõ és alsó számjegyek nem elegendõek a partíció után, add hozzá nullákat.
3. A táblázatban határozza meg a pár, a triádok, a tetrádok stb. Értékét. biteket, amelyek a bináris rendszerben vannak írva, annak a rendszernek az értéke szerint, amelybe lefordítjuk.
Például, a 1111010111010.0111 számú számot a bináris rendszerbe írva. Alakításra oktális számrendszer felosztja a számot triádok (hiszen száma 2 alap egyenlő 3), a helyeken, jobbra és balra: 1.111.010.111.010,011.1. A partíciót pontok mutatják. Az idősebb és a kisebb triádoknál nincs elegendő kibocsátás. Hozzáadjuk nullával: 001.111.010.111.010,011.100. A táblázat szerint meghatározzuk a triádoknak megfelelő oktális számokat. Az oktális szám 17272,34.
Tekintsünk még egy példát: a 1111010111010,0111 számú számot a bináris rendszerben írva. A hexadecimális számrendszerbe történő fordításhoz ossza a számot tetradoknak (mivel a 2-es szám alapja 4): 1.1110.1011.1010.0111. A magas rangú tetrádban nincs elegendő vízkibocsátás. Adjuk hozzá nullákkal: 0001.1110.1011.1010,0111. Az asztalról a tetradoknak megfelelő hexadecimális karaktereket határozzuk meg. Kiderül a hexadecimális szám 1EBA, 7. Adjon ugyanazt a számot. A kvaterner számrendszerbe történő fordításához osztja a számot párokra (mivel a 2-es szám alapja 2): 1.11.10.10.11.10.10,01.11. Az idősebb párban egy bitet nem elég. Töltsük fel nullával: 01.11.10.10.11.10.10,01.11. Határozza meg a párnak megfelelő négyjegyű számokat. Az 1322322.13 számú kvaterner számot kapjuk.
A fordított fordítás végrehajtása:
Tegyük fel, hogy több 73,62-et kapott. oktális jelölésű. Szükséges egy bináris rendszerre fordítani. Ehhez a szám minden számjegyét 0 és 1 hármas sorba írjuk, ami megfelel az oktális számnak a bináris rendszerben: 111.011.110.010.
Vegyünk egy másik példát: a 7B3, E6 számot hexadecimális jelöléssel írva. Szükséges egy bináris rendszerre fordítani. Ehhez a hexadecimális szám minden egyes számjegyét 0 és 1 tetrad számmal írjuk, ami a bináris rendszerben lévő jel értéke: 0111.1011.0011,1110.0110.
Számok fordítása a p-pozíciós számrendszerről a decimálisra.
Minden olyan helymeghatározó rendszer, amelyről beszéltünk, egy általános elvre épül. Bizonyos számú p-t választunk, a számrendszer alapját, és minden N számot az együtthatókkal rendelkező hatásainak kombinációjával ábrázoljuk. egy tetszőleges szám a számrendszerben a p alapon a következő formában van:
Ha a 1011011,11 bináris számot tizedes rendszerre szeretné konvertálni, akkor használja ezt a képletet. A rendszer alapja p = 2, k a vessző bal oldalán lévő karakterek számát jelző koefficiens, k = 7; a a megfelelő együtthatókkal rendelkező szám jelei.
A képlet segítségével konvertáljuk a BF, 1D hexadecimális számot a decimális rendszerbe. A rendszer alapja p = 16, k = 2.
Legyen szükség a 254 262 oktális szám lefordítására egy tizedes rendszerbe. A rendszer alapja p = 8, k = 3