A szögméretek tűréseinek rendszere
Elfogadható a szögméretek megosztása:
- a síkban lévő szögekhez. Két sugarból áll, amelyek egyetlen pontból származnak;
- dihedral szögek. Két síkból alakult ki, amelyek egyenes vonalból (él) származnak. Azonban a mérés megkönnyítése érdekében a pontossági követelmények a síkban lévő szögre vonatkoznak. azaz az a szög, amelyet a dihedral szögnek az él szélére merőleges síkjával metszi;
- a kúpok szöge a leggyakoribb csoport.
A tervezés során használt összes szokásos szög három csoportra osztható:
· Általános célú szögek - a leggyakoribb csoport, amely magában foglalja a síkban a normál szögeket, a kúpok és a normál kúpok szögeit, a prizmás elemek szögeit (64.
· A speciális célú normál szögek - korlátozottan alkalmazhatók szabványosított speciális alkatrészeknél; Ezek közé tartoznak a speciális célú szalagok szögei és lejtői;
· Különleges szögek - ezek magukban foglalják először a szögeket, amelyek méretei a számított függőségekhez kapcsolódnak más elfogadott méretekkel, és amelyek nem lehetnek normális szögekbe kerekítve; másodszor pedig az egyes működési vagy technológiai követelmények által meghatározott szögek.
A kúpok szögei a szög nagysága, a kúposság, a C betű vagy az i. A kúposság és a lejtés összefügg a kúp alapvető dimenzióival.
Ábra. 64. A fő méretek: a - a kúp; b - prizma elem
Egyenes, kör alakú kúpos felület (a továbbiakban kúpfelület vagy egyszerűen egy kúp) egy egyenes generátorral kapott forradalom felülete, amely a tengelyhez képest elforgatja és metszi.
A kúp fő méretei (64. ábra, a): egy nagy alap átmérője egy kis bázis D. átmérője d. kúpszög # 945; (tervezési forma), dőlésszög # 945; / 2, a kúp L. hossza
A kúp alja alatt olyan kúpokat értünk, amelyek egy kúpos felület merőleges síkjai által alkotott keresztmetszet által alkotnak, amely tengelyirányban határolja.
Ha figyelembe vesszük a kúpos ízületek tűréseit és kirakodását, használja az alábbiakban felsorolt kifejezéseket (65.
A fő sík a kúp keresztmetszete síkja, amelyben a kúp névleges átmérője be van állítva.
Az alapsík a kúp tengelyére merőleges sík, és meghatározza a fő sík tengelyirányú helyzetét vagy az adott kúp tengelyirányú helyzetét a kúp kúphoz viszonyítva.
Alapként válasszon a kúp bármelyik vállának, vállának vagy áthelyezésének végét a hengerbe, leggyakrabban a nagy átmérő oldalán. A kúp alap- és alapszintje egybeeshet.
A kúp vagy a zi közötti távolság a kúp alap- és alapszintje közötti távolság. A külső kúp kiindulási távolságát ze jelöli. a belső kúp alapvonala zi.
Ábra. 65. A főbb paraméterek: a - a belső kúp; b - a külső kúp;
c - kúpos kapcsolat
A Conicity C a két keresztmetszet közötti különbség aránya a köztük lévő távolság között.
A C konikust a meghatározás szerint a következő képlet segítségével számítjuk ki: C = (D - d) / L = 2tg.
A kúposságot gyakran 1: x arányként jelöljük. ahol x a kúp keresztmetszete közötti távolság, amelynek átmérője 1 mm, például C = 1:20.
A lejtési szög (lejtés) a D, d, L dimenziókhoz kapcsolódik:
A felcserélhetőség érdekében a normál szalagok sorai létre lettek hozva (GOST 8593). Különleges kúpos kúpok vannak műszeres kúpokhoz: Morse kúpok 0,1,2,3,4,5,6; A Morse-kúpok csonka - B 7, B 10, B 12, B 16, B 18, B 22, B 24, B 32, B 45; a kúpok metrikusak.
A kúpos felületeknél az univerzális méretek mérésénél a 6. ábrán feltüntetett méretek beállítása javasolt.
A nemzetközi egységrendszerben (SI) a sík szög mértékegységére vonatkozóan a radián két sugár közötti szög, amely a kör kerületén egy ívet vág, amelynek hossza egyenlő a sugárral.
Azonban a mértékegységen alapuló egységek rendszere sokkal kényelmesebb a méréseknél. amelyben egy fokot használnak a szög olvasásához. perc. második. Egy fok és egy radian közötti kapcsolat: 1 rad = 57 0 17 '45 ".
Ezenkívül a szög meghatározható a dimenzió egy bizonyos hosszúságú lineáris mérésben történő növelésével, például a prizma elem lejtésével.
a - a külső kúpra; b - a belső kónuszon
A szabványos GOST 8908 három szögletes mértékegységben megadott szögértékek három csoportját biztosítja és 17 pontossági fokot állít be. pontosság csökkenő sorrendben: AT 1, AT 2, AT 3, ... AT 17. A latin betűk AT jelölik a szögeltolódást - a legnagyobb és a legkisebb margó közötti különbséget (megengedett szögek). Amikor egyik fokról a másikra halad, a tolerancia értéke geometrikusan változik a nevezővel # 966; = 1,6.
A valóban elérhető pontossági fokozatok alkalmazása:
1-4 - tartalék fok;
5 - kúpos mérőkhöz - dugók;
6 - ferde kaliberekhez;
7, 8 - nagy pontosság (szerszámok kúpjai, tengelyek és tengelyek kúpos vége a pontosan központosított részekre);
9 -12 - normál pontosság (középső fészkek és középpontok, szögletes rések az útmutatókban stb.);
13-15 - csökkentett pontosság;
16-17 szabad méretekben.
Az egyes pontossági fokozatokra a négy dimenziójú tűréshatár vonatkozik (67. ábra):
AT # 945; - a sugár mértékében kifejezett szögeltolódás (pl. AT 17 = 80000 mrad), és a pontos érték, amelyet fokméretben mértek (például AT 17 = 4 # 730; 35 # 900; 01 # 733;);
AT # 945; # 900; - tolerancia, fokokban kifejezve, de kerekített értékkel a radianumban kifejezett kifejezéshez képest. Így a pontossági fok 17-es szöge megegyezik az AT 17 = 4 # 730; A rajzokon ajánlott feltüntetni a szög kerek tűrését;
ATh a lineáris mérésben kifejezett tűrés (μm) a szegmens hossza az AT # 945 szöggel szemben lévő szög rövid oldalára merőleges; ezen szög csúcsától L1 távolságra;
A kúpszög ATD - tűrése, lineárisan kifejezve, a kúpos tengely két normál szakaszában lévő átmérők különbségében egymáshoz képest egy adott távolságban lévő síkokból; a kúp tengelyére merőleges irányban határozzák meg.
A kezdeti értékek AT # 945; mikroradiánokban; ezek alapján az AT # 945 szögek tűréseinek kerekített értékeit kaptuk; # 900; fokokban, percekben, másodpercekben, a rajzokon látható módon. Emellett ugyanazokat a toleranciákat adják meg ATh (prismatikus elemek) és ATD (kúpos felületek) lineáris értékei formájában. A legutóbbi tűréshatárokat a szögeltérések közvetett irányítására használják.
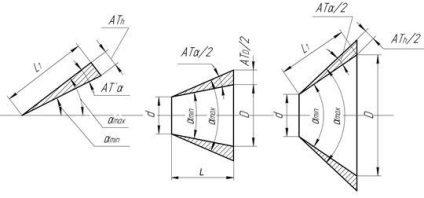
Ábra. 67. A szögek tűréseinek típusai:
a - szögeltolódás; b - C £ 1: 3 kúpossága; c - a C> 1: 3 kúp alakú
szögek előírt tűréseken: a kúp a kúposság kisebb, mint 1: 3 - attól függően, hogy a kúposság L hossza, mert kúpok a kúposságú, mint 1: 3 - attól függően, hogy a hossza a alkotója a kúp L1; a prizmás elemek szögeihez - a szög kisebb oldalának hosszától függően.
Így a szögek és a lineáris egységek szögének tűrése közötti összefüggést a következő képlet határozza meg:
Az 1: 3-nál nagyobb kúposságú kúpokhoz az ATD értéket az alábbi képlet határozza meg:
ahol a a kúp névleges szöge. Kis szögek esetén (C £ 1: 3): ATD @ ATh.
A tolerancia mezőnek három fő típusa van a névleges szöghez képest: plusz (+ AT), mínusz (+ AT) és szimmetrikus (± AT / 2).
Ábra. 68. A prismatag szögének tolerancia mezők helyének típusai:
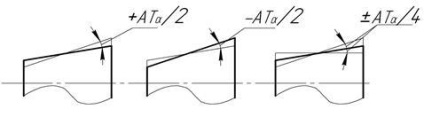
Ábra. 69. Tengerszintek elrendezésének típusai a kúpszögnél:
A tolerancia mező bármely elrendezésére a szögméretek eltéréseit a névleges szögmérettől mérjük. A prismatikus elem szögének toleranciatartományainak elrendezését a 3. ábrán mutatjuk be. 68, és a kúpszög - a 69. ábra.