Energiahatás
A potenciális vonzás energia negatív, és a párosítás a két normál elektron csökkenti az energia, ahol is az energia között rés van kialakítva a páros és páratlan elektronok. Mivel a páratlan elektronok egyenként tekintendők, ezt az energiát általában 2Δ jelöli, ahol Δ az elektronenkénti energiahézag
pár. Az energiahézag csökken a Tcr kritikus hőmérséklet közeledtével, és Tcr értékre nullává válik. ОK esetében a 2Δ értéke megközelítőleg
Az elektronok, amelyek a párt alkotják, nagy távolságra vannak egymástól,
interatomikus távolságok, vagyis a mikrométer sorrendjének távolságai. Ez az eredmény azt mutatja, hogy a párosítás az elektronok nem következménye az interakció egyetlen ion a kristályrács oldalon, és eredményeként keletkezik a kollektív kölcsönhatás sok csomópont. Mivel a párok elektronjainak távolsága 1 μm-es nagyságrendben van, e távolságon belül a pólus elektronmozgása szigorúan korrelált és kölcsönösen koherens. Ez a korreláció a hosszú távú rend korrelációja, és a koherencia hosszaknak nevezett távolságra kiterjed.
Így a koherencia hossza (ξ) a Cooper pár jellegzetes mérete (általában 0,1-1 μm).
Egy normál fémben a szabad elektront az alak hullámfüggvénye képviseli
Ha egy elektron a szétszóródást tapasztalja, a hullámvektor (k) megváltozik, és a hullám fázisa (k • r) ugrik. Ezért, egy szabad elektron egy fémben való mozgásának folyamatában, annak fázisa véletlenszerű változások sorozata. Egyetlen elektron esetében az elektron egy fázisának ismeretében egyetlen értéket nem lehet megjósolni.
A szupravezető párt az hullámfüggvény is leírja a hullámvektorral
(k) a pár két elektronjának mozgását ábrázolja.
Az elektronpár azonban szétszóródás nélkül mozog (szupravezetés!) És ezért a fázis (k • r) nem tapasztalja a véletlenszerű ugrásokat. A Cooper páros fázisának ismeretében egy ponton meg lehet becsülni értékét a másikban. Fázis változás, amikor mozog egy pont egy pár rádiuszvektorhoz r1, hogy a pont a rádiuszvektorhoz r2 k-val egyenlő (r2 -R 1) függetlenül a távolság | r2 -G 1 |.
A szupravezető elektronpár fázisának rendszeres megváltozásának jelenségét fázis koherenciának nevezzük. Rendkívül fontos szerepet játszik a szupravezetés jelenségeiben.
Mágneses fluxus kvantálása.
Vegyünk egy gyűrűs vezetőt, amelyen át szupravezető áram van.
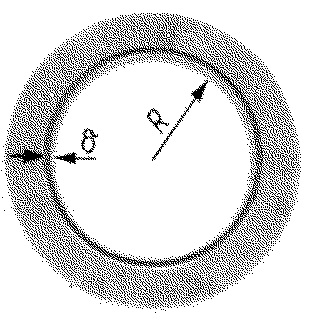
Ábra. 1 Keresztmetszet a gyűrűs vezeték közepes síkjában. R a szakasz belső körének sugara, δ a felületi réteg vastagsága, amelyben a szupravezető áram koncentrálódik.
Legyen $ a mágneses fluxus a gyűrűs karmester belső kerületével határolt felületen keresztül. Mivel a szupravezető jelenlegi álló és ott a végtelenségig, de azt is előírja a fázis koherencia mozgás szupravezető pár hordozó aktuális indokolt előírni, hogy a fázist megváltozott 2π egész szám, amikor áthaladó belső kerülete, azaz a 2π, 4π, 6π, stb. értékeket veszi fel.
ahol n értéke 1, 2, 3, stb., és az integrált értéket az R sugarú kör L körén belül kell kiszámítani.
A további számítások kell kapcsolnia a hullám vektor (k) a szupravezető áramsűrűség Ic, és a mágneses fluxus F. Vegyük integrációs áramkör L (6) a kör sugara (R + δ), ahol a δ - vastagsága a felületi réteg, ahol a szupravezető aktuális koncentrálódik , átfogjuk az egész szupravezető áramot és az általa előállított teljes fluxust. Ezen a vonalon lévő vezetéken belül L az Ic = 0 szupravezető áramsűrűség.
Ennek szem előtt tartásával a számítások azt mutatják, hogy a szupravezető zárt hurkon átnyúló felületen lévő mágneses fluxus diszkréten változik, azaz a a mágneses fluxust kvantálják. A mágneses fluxus Ф0 mennyisége egy alapvető mennyiség, amelyet csak a világállandók határoznak meg. Az értéke nagyon kicsi:
Ф0 = πħ / e = 2,07 • 10 -15 Vb. (7)
Ennek megfelelően a mágneses fluxus a felületen keresztül van
a mínusz jel jelenik meg, mert az elektron töltése negatív, és e az elektron töltési modulusa.
A kísérletben megbízhatóan meghatároztuk a mágneses fluxus kvantálását, és mértük a mágneses fluxus kvantumát. Ezeknek a méréseknek az eredményei megbízható kísérlettel igazolják, hogy a szupravezető áram az elektronpárok mozgása, és nem az egyes elektronok mozgása miatt következik be.