A rugalmas szerkezeti elemek merevsége
Mátrix formában írhatjuk őket:
- a megfelelés mátrixa (négyzetes méretű mátrix (6x6);
() a megfelelőségi mátrix elemei.
A megfelelés mátrixa # 916; egyértelműen és teljesen leírja a vizsgált rugalmas elem (ebben az esetben a rudat) merevségi jellemzőit.
A megfeleltetési mátrix eleme () egy olyan szám, amely számszerűen egyenlő az elmozdulással a -th irányban egy-egy irányú erő hatására:
- Az átlós elemek jellemzik, hogy a rúd megfelel a cselekvő erő irányában;
amikor - ezek az elemek jellemzik a rúd lineáris megfelelését (az elemek mérete [m / H]);
- ezek az elemek jellemzik a rúd szögletes megfelelését (az elemek mérete [1 / mN]);
címen. és mikor. - ezek az elemek jellemzik a pólus szög- és lineáris elmozdulása közötti keresztkötéseket (az elemek mérete [1 / H]).
A Morale integrál, amely leírja a rugalmas rúd tetszőleges pontjának elmozdulását () egy külső terhelés hatására,
ahol - a külső terhelés hatásából származó megfelelő belső erők;
() - az egyetlen terhelés pólusában fellépő hatásból származó megfelelő belső erők ().
A Moore integrál és a (1.5) kifejezés alapján írjuk le a megfelelőségi mátrix elemeinek () meghatározására szolgáló képletet:
Az (1.6) kifejezés szerint nyilvánvaló, hogy ().
Visszatérünk a kifejezéshez (1.4):
Szorozzuk meg a kifejezés bal és jobb oldalát (2.1.)
Ezután a merevségi mátrixot jelöli, megkapjuk az egyensúlyi egyenletet a mátrix formában
Itt van a kisméretű mátrix (az almatrix meghatározója, amelyet ebből a mátrixból az i. Sor és az i. Oszlop törlésével kaptunk).
Példa az egyenes vonalú rúd megfelelőségi mátrixának kiszámítására:
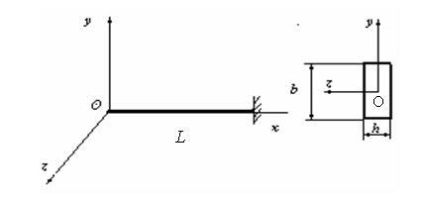
A vizsgált esetben
1. Tekintsük az esetet, amikor i = 1.
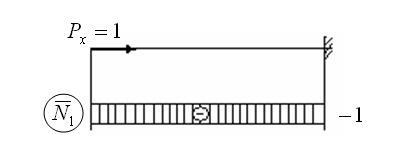
2. Tekintsük azt az esetet, amikor i = 2
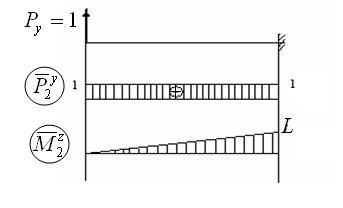
3. Tekintsük azt az esetet, ahol i = 3:
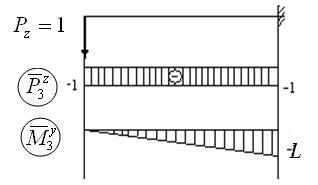
4. Tekintsük azt az esetet, amikor i = 4:
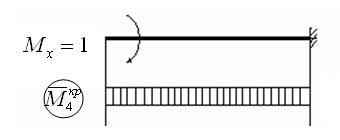
5. Tekintsük azt az esetet, amikor i = 5:
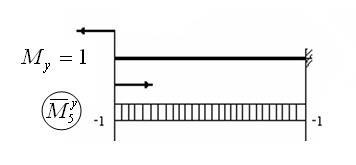
6. Tekintsük azt az esetet, amikor i = 6:
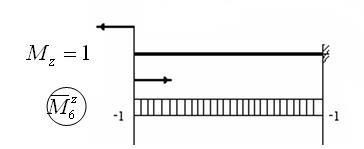
Ezután az (1.6) képlet szerint:
Tekintsük egy egyenes vonalú rugalmas elem megfelelőségi mátrixát, amelynek hosszúságú változója van. A rugalmas elem két részből áll: M és E.
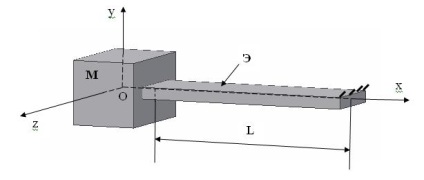
Az Oxyz-koordinátarendszerben a megfelelőségi mátrixot tekintjük.
- a tehetetlenségi tömeg keresztmetszete;
- a rugalmas elem keresztmetszete;
Tekintsünk néhány egyenletes és furcsa funkciót.
1) Ha A (x) egy pontos függvény, azaz A (x) = A (-x) (például A (x) = x 2), akkor.
2) Ha A (x) egy furcsa függvény, pl. A (x) = -A (-x) (például A (x) = x),
Ha a pólust a rúd közepére (;) helyezzük, akkor egy furcsa függvény tulajdonát használva írhatunk
Ez azt jelenti, hogy ha az egyenes rúdnak állandó keresztmetszete van a rúd hosszán, és a pólus középen helyezkedik el, és mereven csatlakozik a rúd laza végéhez, akkor a megfelelőségi mátrix átlós alakú.
Átlós megfeleltetési mátrix esetén a pólus elmozdulása csak az erő hatására irányul.
Az állandó keresztmetszetű rugalmas elemek esetében, amikor a pólus elrendezése a nem deformálódott pálca középpontjával egybeeső ponttal történik, a következőket kapjuk:
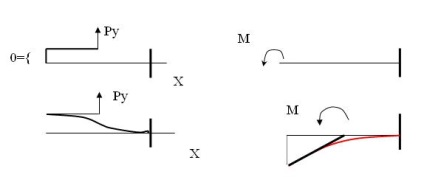
Egy koordináta-rendszert, amelyben a rugalmas elemnek a megfelelés mátrixa átlós formában van, normális koordináták rendszere.
A normál koordináták rendszerében a póluson lévő általánosított erő hatására az elmozdulás csak az erő hatásának irányában következik be
Meghatározzuk a konstans szakasz RE metszési mátrixának elemeit egy koordináta-rendszerben a tengelyekhez viszonyítva és amelynek középpontjában az RE szimmetriája van.
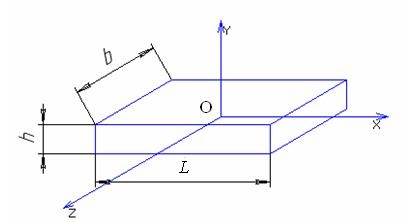
Egy adott UE esetében a megfeleltetési mátrix diagonális alakja lesz.