Röviden a trigonometrikus funkciókról
Az alábbi szöveg a "Az első lépés a mennyiségi valóság" című könyv részét képezi.
4. A trigonometrikus funkciók általánossága minden szög esetén.
Ellenőrizze önmagát, hogy a fentiek szerint a trigonometrikus függvények mindegyike érvényes az ábrán látható helyzetre:
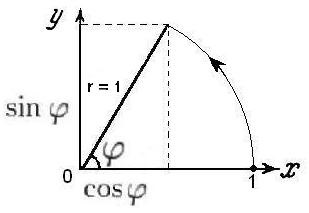
- a téglalap alakú háromszög φ szöge csúcsa egybeesik a származással,
- a háromszög hipotenusza, amely szintén a kör sugara, egyenlő az egységgel, r = 1,
- a koszinusz a sugár sugara az x tengelyen,
- A szinusz a sugár sugara az ordinát tengelyén.
Mindez helyes, de eddig csak az akut szögeknél, amikor a sugár-hypotenuse az első negyedévben van.
A helyzetnek a szögek esetére történő generalizálása nyilvánvaló módon az ábrából következik:
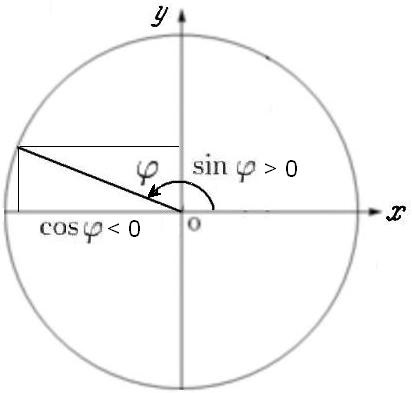
Nevezetesen, bármilyen szögben koszinusz, - vetítőkészülék sugara a vízszintes tengelyen (O x), a szinusz - vetítőkészülék sugara a függőleges tengelyen (O y), sőt azokban az esetekben, ha a vetítési belép a negatív tartományban a koordinátatengelyek, tulajdonított funkciókat jele mínusz.
Minden más trigonometrikus függvényt a szin és a kosinus kifejezésekben fejezzük ki, a megfelelő képleteket a fentiekben adjuk meg.
A trigonometrikus függvények legfontosabb tulajdonságai és grafikonjai
Az f (x) függvényt akkor is mondjuk, ha f (-x) = f (x), és furcsa, ha f (-x) = -f (x).
Az egyenletes függvény görbéje szimmetrikus az ordinát tengely (O y) függvényében, és egy furcsa függvény grafikonja szimmetrikus a származás tekintetében. A grafikonok azt mutatják, hogy a koszinusz egyenletes, és a szinusz, a tangens és a cotangent furcsa.
A legtöbb funkció sem egyenletes, sem furcsa, ezek a két kifejezés összege:
Az első kifejezés az egyenletes rész, a második kifejezés furcsa rész.
De az alapvető trigonometrikus funkciók - mint láttuk - nagyon határozott paritást jelentenek.
5. Mi szükséges ahhoz, hogy emlékezzen a trigonometrikus funkciókra.
Először is, a szinusz és a koszinusz általános definíciója.
Ebből következik, hogy például a negyedik negyedévben a koszinusz pozitív, a szin negatív, vagy a 180 ° -os szinusz nulla, a koszinusz mínusz egy. És így tovább.
Az is hasznos, hogy képes legyen felhívni grafikonok a szinusz, koszinusz, tangens és kotangens a kötelező értékek jelzésére az x és y-tengelyek, ahogy az ábrákon is látható a táblázatban mutatjuk be.
Még mindig nagyon fontos képletek:
Az utolsó két képlet egyszerűen rekonstruálható az egyenletből:
Ezenkívül hasznos megjegyezni a trigonometrikus függvények paritás-páratlanságát és ismereteiket.
Szintén hasznos vezetés formulák, amelyek lehetővé teszik számunkra, hogy kifejezzék az értékeket trigonometrikus függvények bármilyen szögben az első negyedévben az értékek trigonometrikus függvények szögek.
Az ilyen számítások szükségességének elkerülése érdekében alkalmazza az mnemonikus szabályt:
1. Ha a szögek trigonometrikus funkciói 90 ° ± a vagy 270 ° ± α. akkor a szinusz a koszinuszra, a koszinuszra szinuszra változik, a cotangentumhoz érintkezik, a tangens csúcsa. A 180 ° ± α vagy 360 ° ± α szögek esetén a funkciók változatlanok maradnak, pl. a szinusz sinus marad, stb.
2. Az eredmény jele megegyezik azzal a negyedév eredeti funkciójával, amelyre a kezdeti szög csökken.
Például: cos (180 ° - α) = - cos α.
A koszinusz koszinusz marad, mivel 180 °, nem 90 ° vagy 270 °.
A második negyedév kezdeti szöge (180 ° - α), ahol a koszinusz, a kezdeti funkció negatív, ezért a mínusz jel.
Itt talán ez minden!
Nézd meg, hány trigonometrikus képlet van a könyvtárban! De szinte az összes alap formulát könnyedén szerezhetjük meg egy vagy két akcióból azokból a kapcsolatokból, amelyeket figyelembe vettünk.
Ezért a legegyszerűbb nem a trigonometrikus képleteket megtanulni, de szükség szerint kiadni.
Persze, nem bántana, hogy jobban megismerje a trigonometria, de itt van a szükséges minimum. Ha további olvasásra van szükség, további magyarázatokat kell adni.