Nyitott matematika leckét az általános iskolában
- iskolai:
- Hasonlítsa össze a különböző típusú mozgásokat. egymást követve, ellentétes irányban, késéssel.
- Meghatározni a megközelítés, eltávolítás utáni és utáni sebesség felderítésére vonatkozó szabályokat; az S, t és v fizikai mennyiségek közötti kapcsolat (szóbeli formulációk)
- iskolai:
- Képzeld el képességeidet egy szokatlan helyzetben.
- A tantárgy tisztelete, a matematikai problémák felismerésének lehetősége a környező világban.
- fejlődő:
- A problémák megoldásának különböző módjainak és a racionális megoldások elosztásának felkutatása;
- fejleszteni a diákok térbeli képzeletét, a képzeletbeli gondolkodást;
- javítja a grafikai kultúrát.
- A tábla bejegyzése;
- Támogatási rendszerek; formula.
- Nyomtatás szimulátor, teszt.
- Számítógép, multimédiás kivetítő, képernyő, a rajzfilm "A hibák oka".
A lecke megkezdődik.
Engedje el a fiúknak, hogy késõbb használják!
Nézzétek meg alaposan a képernyőt. (A hibák szigetéről szóló rajzfilm részlete). Mit mondasz? Miért történt a baj? (Helytelenül megoldotta a problémát).
Sorokin Kolya rajzfilm hősének sikerült kijavítania a helyzetet, de a való életben nem mindig lehetséges a hibák kijavítása, ezért el kell dönteni, átgondolni, megérteni különböző élethelyzeteket.
Mit szeretne tanulni ma az osztályban, mit tanulni? (Megoldja a mozgás feladatait, töltse ki feladatait a mozgáshoz). Ezen vagy a következő leckéket együtt fogjuk próbálni a kérdések megválaszolására.
A TANULMÁNY TÉMA "A mozgás problémáinak megoldása" (3. dia)
Milyen feladatok vannak a mozgalom számára?
- Mozgás az ellenkező irányba eltávolítással
- Mozgás az ellenkező irányba egymás felé
- Mozgás egy irányban egy késéssel
- Mozgás egy irányba utána
Mi a közös és mi a különbség ezeken a feladatokon? (4. dia)
- KÖZÖS: vannak mozgó tárgyak, vannak mennyiségek: sebesség, idő, távolság
- DIFFERENCIÁK: a tárgyak mozgásának iránya, a mennyiségi értékek és a mérési egységek kiindulási helye.
- Az alapismeretek rendszer aktualizálása (5. dia).
(Az értékek közötti sebesség ismétlése: sebesség, idő, távolság)
- Ne feledje, hogyan kell megtalálni
- SPEED V = S: t
- TIME t = S: V
- DISTANCE S = V × t
- Végezze el a szimulátor feladatait. A felső vonalat együttesen hajtják végre, a többiek párban vannak. (6. dia)
s = 60 km
t = 12 perc
v -?
5 km / perc
Önteszt: (7. dia). Teszteld a munkádat.
- Ki hibázott? Miért fordult elő a hiba?
- Ki hibáztatott? JÓ FELLOWS!
- Szisztematikus rögzítés. Munka a tankönyvvel. (8., 9. dia)
Kezdjük megoldani a nehezebb problémákat. Nyissa meg a bemutatót a következő oldalon: p. Olvassa el a 485 feladat szövegét önállóan.
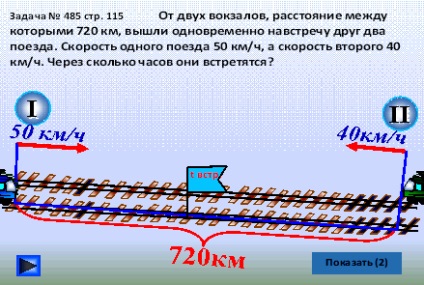
- Olvassa el, hogy Petya megoldotta a problémát.
- Nyissa meg a feladatkönyvet.
- Írja le a probléma megoldását a táblán és a notebookon.
1) 50 + 40 = 90 (km / h) - megközelítési sebesség
2) 720: 90 = 8 (h)
Válasz: 8 óra alatt a vonatok találkoznak.
Érdekes Varvara balra néz, jobbra néz,
Balra néz, jobbra néz.
És aztán előre, itt egy kicsit pihentek.
Mi van a bal oldalon, mi van a jobb oldalon?
Balra, jobbra, balra, jobbra.
És aztán előre, itt egy kicsit pihentek.
Hirtelen Varvara mindenfelé felfelé néz.
Visszatér, a kikapcsolódás szép.
És most nézzük le - a nyak izmainak feszülnek.
Visszatér, a kikapcsolódás szép.
Fel és le, fel és le. Most mosolyogj a szomszédodra.
- A hangulat? (Jó!)
- Lába? (Helyben!)
- Hands? (Helyben!)
- Könyök? (A szélén!)
- A vissza? (Közvetlen!)
- Rendszeres rögzítés (11. dia)
- Lehet-e saját feladatot létrehozni? Hogyan?
- Mit kell tenni ehhez? (Válassza ki a mozgás tárgyait, a mozgás irányát, az indulás helyét, adja meg a mennyiségek mérésének értékét, határozza meg, hogy mit keresnek)
- A feladat felépítése a forgalmi mintának megfelelően: (12. dia)
- Meghatározza a feladat típusát?
- Mi a probléma ismerete?
- Mit kell találnom?

A két város közül a távolság 65 km, két kocsi egyidejűleg ellentétes irányban. Egyikük 80 km / h sebességgel utazott, a másik pedig 110 km / h sebességgel. Mennyire távolabb lesznek az autók az indulás után 3 órával?
- Terv kidolgozása a probléma megoldására (2 szempont)
Írjon megoldást bármilyen módon
80 * 3 = 240 (km)
110 * 3 = 330 (km)
240 + 330 = 570 (km)
570 + 65 = 635 (km)
(80 + 110) = 190 (km / h)
190 * 3 = 570 (km)
570 + 65 = 635 (km)