Nyilvános kulcs titkosítás
A nyilvános kulcs titkosítása
A szimmetrikus titkosítási kulcstól eltérően nem találjuk a nyilvános kulcsú titkosítás történeti használatát. Ez egy viszonylag új koncepció.
A szimmetrikus kriptográfia jól illeszkedik olyan szervezetekhez, mint a kormányok, a katonai és a nagy pénzügyi vállalatok, amelyek titkos kapcsolatba kerülnek.
Az elmúlt néhány évtizedben egyre kevésbé tesztelt számítógépes hálózatok elterjedése miatt az igazi szükségletet a nagyobb titkosítású kriptográfia használatára érezték. A szimmetrikus kulcsot nem találták praktikusnak a kulcskezeléssel szembesülő problémák miatt. Ez nyitott kriptoszisztéma kulcshoz vezetett.
A titkosítás és dekódolás folyamatát a következő ábrán mutatjuk be -
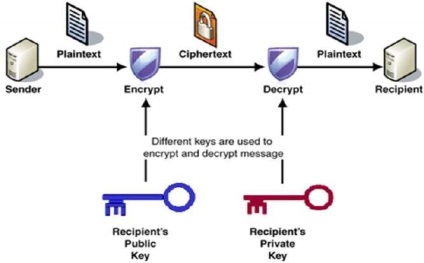
A nyilvános titkosítás kulcsrendszerének legfontosabb tulajdonságai -
Különböző kulcsokat használnak a titkosításhoz és a dekódoláshoz. Ez a tulajdonság, állítsa be ezt a sémát, amely eltér a szimmetrikus titkosítási sémától.
Minden egyes vevőegységnek van egy egyedi titkosítási kulcsa, amelyet általában privát kulcsnak neveznek.
A nyilvános kulcs hitelességének bizonyos garanciái szükségesek ebben a rendszerben, hogy elkerüljék az ellenség helyettesítését vevőként. Általában ez a típusú kriptográfiai rendszer magában foglal egy megbízható harmadik félt, amely tanúsítja, hogy egy adott nyilvános kulcs csak egy adott személyhez vagy entitáshoz tartozik.
A titkosítási algoritmus elég összetett ahhoz, hogy tiltsa a titkosítást a nyitott szöveg törléséből, a titkosítási kulcsból és a titkosító kulcsból (nyilvános kulcs).
Bár a magán- és a nyilvános kulcsok matematikailag kapcsolódnak egymáshoz, a nyilvános kulcs kiszámítása nem lehetséges. Valójában a nyilvános kulcsú kriptográfiai rendszer intellektuális része a két kulcs közötti kapcsolat kialakításában.
Háromféle nyilvános kulcs titkosítási rendszer létezik. A következő fejezetekben megvitatjuk őket -
RSA Cryptosystem
Ez a kriptoszisztéma egyike az eredeti rendszernek. Még ma is a legforgalmasabb kriptográfiai rendszer. A rendszert három tudós, a Rivest, Adi Shamir és Len Adleman és a. ezért RSA-kriptográfusnak hívják.
Az RSA kriptográfiai rendszerének két aspektusa látható, először egy kulcspárt, másodsorban titkosítási és dekódolási algoritmust generálunk.
RSA kulcspár létrehozása
Minden olyan személy vagy fél, aki a titkosítás használatával kapcsolatban kíván részt venni, kulcsot kell létrehoznia, nevezetesen egy nyilvános kulcsot és egy privát kulcsot. A gombok létrehozásában követett folyamat az alábbiakban olvasható:
Form RSA modul (n)
Válasszon két nagy kezdőszámot p és q.
Számítsd ki az n = p * q értéket. Az erős, összetörhetetlen titkosításhoz n nagy mennyiségeket, általában nem kevesebb, mint 512 bit.
Keresse meg a számot (Származtatott f)
A számnak 1-nél vagy annál kisebbnek kell lennie. mint (p - 1) (Q - 1).
Nem szabad olyan közös tényező, hogy e és (p - 1) (q - 1), azzal az eltéréssel, 1. Más szóval, a két szám és e (p - 1) (q - 1) viszonylag fix.
Nyilvános kulcs formája
Egy pár szám (n, e) képezi az RSA nyilvános kulcsát, és nyilvánosságra kerül.
Érdekes, hogy bár n egy nyilvános kulcs része, a nagy elsőszámú faktorálás nehézsége biztosítja, hogy egy támadó nem talál két véges számot egy véges időben (p Q), amelyet n megszerezni. Ez az RSA ereje.
Privát kulcs létrehozása
A d magánkulcsot p, q, e-ből számítjuk ki. Egy adott n és e esetében egy egyedi szám d.
A d szám az inverz modulo e (p - 1) (q - 1). Ez azt jelenti, hogy a szám d kisebb, mint (p - 1) (Q - 1) úgy, hogy amikor megszorozva e, egyenlő 1 mod (p - 1) (q - 1).
Ez a kapcsolat matematikailag az alábbiak szerint íródott:
A kiterjesztett euklideszi algoritmus p, q, e bemenetet és bemeneteket ad, és q kimenetet ad.
Az RSA kulcspárok létrehozásának egyik példája az alábbi. (Az egyszerűség kedvéért a p és q prímszámokat itt kis értékként veszik be, a gyakorlatban ezek az értékek nagyon magasak).
Legyen a két prím p = 7 és g = 13. Így a modul η = PQ = 7 χ 13 = 91.
Kiválasztási e = 5, amely megfelelő-e, mivel nincs olyan szám, amely egy közös tényezője 5, és a (p - 1) (Q - 1) = 6 × 12 = 72 1, azzal a.
Egy pár szám (n, e) = (91, 5) nyilvános kulcsot hoz létre, és elérhetővé tehető azok számára, akik titkosított üzeneteket kívánnak küldeni nekünk.
A kiterjesztett Euklideszi algoritmus p = 7, g = 13 és e = 5 bemenete. A kimeneti jel d = 29.
Győződjön meg róla, hogy a d helyesen értékeli a számítást -
Ezért a közös kulcs (91, 5) és a magánkulcsok (91, 29).
Titkosítás és dekódolás
A kulcspár generálása után a titkosítási és dekódolási folyamat viszonylag egyszerű és számítási szempontból egyszerű.
Érdekes megjegyezni, hogy az RSA nem közvetlenül dolgozik a bitszalagokkal, mint a szimmetrikus titkosítási kulcs esetében. Modulszámok működnek. Ezért szükséges, hogy a szöveges szöveget n számnál kisebb számsorokként ábrázoljuk.
RSA titkosítás
Tegyük fel, hogy a feladó szöveges üzenetet szeretne küldeni olyan személynek, akinek a nyilvános kulcsa (n, e).
Ezután a feladó egy nyitott szöveg, mint n számnál kisebb számsorrend.
Az első nyílt P kód titkosítása, amely egy modulo n szám. A titkosítási folyamat egyszerű matematikai lépés, mint például -
Más szóval, a C rejtjeles szöveg egyenlő a P megnyitott szövegével, amelyet önmagában szorozva, majd visszaállítva modulo n. Ez azt jelenti, hogy a C szintén kisebb, mint n.
Visszatérve a P = 10 nyílt szövegű kulcsok generálásának példájához egy titkosított C -
RSA dekódolás
Az RSA dekripciója szintén nagyon egyszerű. Tegyük fel, hogy a páros (n, e) nyilvános kulcsának címzettje megkapta a titkosított C.
A vevő felveszi C-t a titkos kulcsa erejéig. Az eredmény modulo n a P. szöveges szövege.
Visszatérve a numerikus példánkra, a C = 82 rejtjeles szöveg dekódolásra kerül a 10-es számra, a titkos kulcs 29 -
RSA elemzés
Az RSA-biztonság függ két különálló funkció erősségeitől. Az RSA kriptográfiai rendszer a legelterjedtebb nyilvános kulcsú kriptográfiai rendszer, amelynek ereje a nagyon nagyszámú faktorálás gyakorlati nehézségein alapul.
Titkosítás A függvény egy egyirányú függvénynek tekinthető, amely a nyílt szöveget titkosított formába konvertálja, és csak a titkos kulcs ismeretében törölhető.
Kulcsgenerálás -. A nehéz meghatározni egy titkos kulcsot az RSA nyilvános kulcs megegyezik a faktorizációt modulo n támadó így nem tudja használni ismeretek az RSA nyilvános kulcs határozza meg a titkos RSA kulcsot, ha nem tud figyelembe venni bekezdésben is függvénye egyik módja. , a p és q értékek átadása modulo n egyszerű, de fordítva lehetetlen.
Ha a két funkció közül egyik sem igazolódik egy irányba, akkor az RSA megszakad. Valójában, ha a faktoring módszer hatékonyan fejlődik, az RSA már nem lesz biztonságos.
Az RSA titkosítási erőssége élesen csökken a támadásoktól, ha a p és q szám nem nagy prímszám, és / vagy a nyilvános e kulcsot kis számban választják ki.
ElGamal Cryptosystem
Az RSA mellett más nyilvános kulcsú kriptográfiai rendszerek is javasoltak. Sokan a diszkrét logaritmikus probléma különböző verzióin alapulnak.
ElGamal kriptoszisztémát, amelyet az elliptikus görbe változatnak nevezünk, a probléma diszkrét logaritmusán alapulva. Erőt merít abból a feltételezésből, hogy diszkrét logaritmusok gyakorlati szempontból nem találhatók meg egy adott számra, míg a fordított teljesítményt hatékonyan lehet kiszámítani.
Lássuk át az ElGamal egyszerű változatát, amely egy modulo modulo-val dolgozik. Az elliptikus görbe változatok esetében teljesen eltérő számrendszereken alapul.
ElGamal kulcspárok létrehozása
A kriptoszisztéma minden ElGamal felhasználója kulcspárt generál a következő módon:
A nagy prímszám kiválasztása p. Általában 1024 és 2048 bit hosszúságú elsődleges számot választanak ki.
A generátor elem kiválasztása g.
Ennek a számnak 1 és p - 1 között kell lennie, de nem lehet szám.
Ez a modulo p multiplikatív csoport generátorja. Ez azt jelenti. hogy bármely m-es egész számra p-re vonatkoznak, létezik olyan k egész szám. hogy rk = n mód.
Például a 3 az 5-ös csoport generátoraként (Z 5 =).
Privát kulcs kiválasztása. A privát kulcs x minden szám nagyobb, mint 1 vagy kevesebb. mint a P-1.
Az y nyilvános kulcsérték számítási részét a p, r és az x titkos kulcs paraméterei alapján számítjuk ki. -
A nyilvános kulcs megszerzése. Az ElGamal nyitott kulcs három paraméterből áll (p, r, y).
Például tegyük fel. hogy p = 17. és hogy r = 6 (ezt megerősíthetjük az a tény is, hogy 6 a Z17 csoport generátoraként). Az x titkos kulcs lehet bármely 1-nél nagyobb és 71-nél kisebb szám, ezért az x = 5 értéket választjuk. Az y értékét ezután a következőképpen számítjuk ki:
Így a 62 magánkulcs és a nyilvános kulcs (17, 6, 7).
Titkosítás és dekódolás
Az ElGamal kulcspár generálása viszonylag egyszerűbb, mint az RSA-val azonos eljárás. De a titkosítás és a dekódolás egy kicsit bonyolultabb, mint az RSA.
ElGamal titkosítás
Tegyük fel, hogy a feladó egyszerű szöveges üzenetet szeretne küldeni olyan személynek, akinek ElGamal nyilvános kulcsát (p, r, y), majd -
A feladó egy nyitott szöveg, a modulo p számsorozat formájában.
Az első nyílt P kód titkosítása, amely a modulo modulo p számmal van ábrázolva. A titkosított C előállításához szükséges titkosítási eljárás a következő:
- Véletlenszerűen generálja a k számot;
- Számítsd ki a C1 és C2 értékeket, ahol -
-
Küldje el a C titkosított szöveget, amely két különálló értékből (C1, C2) van elküldve.
A fenti kulcs létrehozására szolgáló ElGamal példánkra való áttéréssel a P = 13 egyszerű szöveg titkosításra kerül az alábbiak szerint:
- Véletlenszerűen generál egy sorozatot, mondjuk, k = 10
- Számítsd ki a C1 és C2 értékeket, ahol -
-
A titkosított szöveg elküldése C = (C1, C2) = (15, 9).
ElGamal dekódolás
A titkosított (C1, C2) dekódolása az x titkos kulccsal történik, a következő két lépés kerül végrehajtásra -
Számítsd ki a moduláris inversion (C1) x modulo p-t, úgy, hogy (C1) -x, mint szabály. a dekódoló tényezőnek nevezik.
Tiszta szöveg legyen a következő képlet segítségével:
Példánkban a C = (C1, C2) = (15, 9) titkosított szöveg dekódolásához az x = 5 titkos kulcs használatával a dekódolási arány
Nyújtsuk ki a P = (9 × 9) modulo 17 = 13 szöveget.
ElGamal Elemzés
Az ElGamal rendszerben minden felhasználó titkos kulcsa x van. és a nyilvános kulcs három összetevőből áll - egy egyszerű modulo p, egy generátor r és egy nyilvános Y = r x I segít. Az ElGamal erőssége a diszkrét logaritmikus probléma összetettségén alapul.
A védett kulcs mérete általában> 1024 bit. Ma 2048 bit hosszú kulcsot használ. Az elülső feldolgozás sebességénél az Elgamal meglehetősen lassú, főleg a legfontosabb hitelesítési protokollokhoz. A nagyobb feldolgozási hatékonyság miatt az ElGamal görbe elliptikus változatai egyre népszerűbbek.
Ellipszis görbék (ECC) titkosítása
Az elliptikus görbékre (cryptography on elliptical curves, cryptography on elliptical curves, ECC) használt kifejezés olyan kriptográfiai eszközök és protokollok készletének leírására szolgál, amelyek biztonsága a diszkrét logaritmikus probléma speciális verzióin alapul. Nem használja a modulo p számokat.
Az ECC olyan számhalmazokon alapul, amelyek elliptikus görbékkel matematikai objektumokkal kapcsolatosak. Vannak szabályok a számok többszörözéséhez és számításához, ahogyan ez a számoknál a modulo p.
Az ECC olyan sok kriptográfiai sémát tartalmaz, amelyet eredetileg moduláris számokra fejlesztettek ki, mint például az ElGamal titkosítás és a digitális aláírás algoritmusa.
Úgy vélik, hogy a diszkrét logaritmust sokkal nehezebb alkalmazni ellipszis görbékre. Ez egy átmenetet indít el a modulo p-től az elliptikus görbékre mutató pontokig. A rövidebb kulcsokkal egyenértékű biztonságot is nyerhetünk, ha a görbe elliptikus variánsait használjuk.
A rövidebb kulcsok két előnyhöz vezetnek:
- A kulcskezelés kényelmessége
- Hatékony számítás
Ezek az előnyök az elliptikus görbét a titkosítási rendszer lehetőségei alapján vonzóvá teszik azoknál az alkalmazásoknál, ahol szűkös számítási erőforrások vannak.
RSA és ElGamal diagramok - összehasonlítás céljából
Röviden össze kell hasonlítani az RSA és az ElGamal rendszerét különböző szempontok alapján.