Csillagközi gázdinamika
A gázdinamika a fizika egyik ága, amely tanulmányozza a gázmozgás törvényeit. Kérdéseivel gázdinamikáról, gyakran találkozunk a mindennapi életben - és ez a fekély-kovye hullámok és csomagolja gyorsan mozgó testek, és a lökéshullámok, melyek a kor szuperszonikus sebességgel jól ismert mindenki számára. De a csillagközi közeg feltételei jelentősen megváltoztatják a gáz mozgásának törvényeit.
Kezdjük hanghullámokkal. Amint az olvasó valószínűleg tudja, a hanghullámok a közegben elterjedt sűrítések és gáz diszperziók sorozatát reprezentálják. Ha finoman nyomja a gázt egy bizonyos kötetet, majd engedte, hogy visszatérjen a sáv, akkor a kezdeti állapotban a tehetetlenség Aztán kissé kitágul, összenyom körülvevő térfogata rétegek hektár, és akkor csökken újra. Vannak olyan ingadozások, amelyeket továbbadnak a szomszédos rétegek, és tőlük - még tovább. Ez a hanghullámok terjedése. Sebességük csak a gáz hőmérsékletétől függ. A léghullámok sebessége 300 K-os hőmérsékleten jól ismert - 330 m / s, és növekvő hőmérséklet mellett a (T) 1/2 arányban növekszik.
De az ilyen hanghullámok adiabatikusak, vagyis azt feltételezzük, hogy a gáz halmozódása és ritmusa hanghullámok nélkül zajlik. Az interstelláris térben ez nem így van. Ahogy a sűrűség nő, a sugárzási veszteségek is jelentősen emelkednek. Ezért a csillagközi hanghullámok semmiképpen sem adiabatikusak. Az első megközelítésben mégis izotermikusnak tekinthetők, vagyis azt feltételezni, hogy amikor a gázt összenyomják és kibővítik, a hullámhőmérséklet egyáltalán nem változik. Ezután a hanghullámok sebessége valamivel kevesebb lesz (levegőben - 20% -kal), és a következő képlet segítségével számítható ki: cs = (RT / mu) 1/2. ahol R az univerzális gáz konstans, és mu a molekulatömeg. Liu bopytno hogy még Newton, aki először számított a sebesség a hanghullám, feltételezhető, hogy izoterm-CIÓ, így sokáig nem értette, miért a hangsebességet a levegőben volt jobb számított Noi. Azonban az interstelláris hanghullámok esetében ez a formula, amelyet Newton szerzett, meglehetősen alkalmazható.
A következő fontos jelenség, amely az interstelláris viszonyok között változik tulajdonságaiban, a lökéshullám. Ennek megmagyarázása érdekében a 6. ábrán bemutatott esetet tekintjük. 16. Egy n1-es és v sebességgel rendelkező gázt egy hosszú csőbe kell vezetni az egyik végén. A falon lebegve meg kell állnia. Stabil gáz keletkezik, amely folyamatosan növekszik, mivel több új gáz kerül be. A pihentető és a mozgó gáz között határos (a 16. ábrán szaggatott) határ van kialakítva, amely a cső irányában mozog a gázáram felé.
Shock wave formation scheme
A határ mögötti gáz koncentrációját n2-nek nevezzük. Kiderült, hogy ha a v sebesség igen magas (sokkal nagyobb, mint a hangsebesség), ez a határ éles (kick-értékes hullám) és a koncentráció a folytatásban, azaz a. E. értéke n2 / n1, korlátozott (például egy atomi gáz n2 / n1 <4, в двухатомном п2 /п1 <6). Объяс-няется это просто. Кинетическая энергия налетающего газа не только сжимает, но и нагревает остановившийся газ. В неподвижной области, таким образом, возникает большое газовое давление, которое и препятствует даль-нейшему сжатию.
De az interstelláris térben ez nem lehet. Amint a gáz összenyomódik, a sugárzása meredeken emelkedik, és a hőmérséklet már nem emelkedik. A gáznyomás kicsi marad, és nem akadályozza meg a gáz további kompresszióját. Ennek eredményeképpen az egymás közti rázkódás-hullámok, amelyeket jobban neveznek "sokkhullámoknak", nagyon nagy koncentrációkon keresztül fordulhatnak elő. Nagysága a folytatásban n2 / n1-casting lehet meghatározni, hogy összehasonlítjuk a gáz nyomása a sűrített domain (azaz. E. arányos értéket n2RT) a sovány dinamikai nyomás ütköző gázáram p1v2 arányos. Így azt állítjuk, hogy az interstelláris lökéshullám koncentrációját az n2 / n1 érték jellemzi
v2 / CS2, ahol T - szokásos Nye csillagközi gáz hőmérséklete (mintegy 10 4 K AOR-megpróbálja HII és sokkal kisebb, mint 10-20 K, in Molecular ob lakkok). Az olvasó könnyen látható, hogy még alacsony sebességei esetén gáz mozgását (például sebességgel 7-8 km / s, - a normál sebesség csillagközi felhők) állíthatjuk elő (amikor ütköznek egymással) tömítést ugrik több tíz vagy akár több száz alkalommal változó koncentráció .
Természetesen az 1. ábrán bemutatott eset is. 16, van egy idealizáció - nincsenek csövek az interstelláris térben, de a mozgás általános jellemzői pontosan ilyenek.
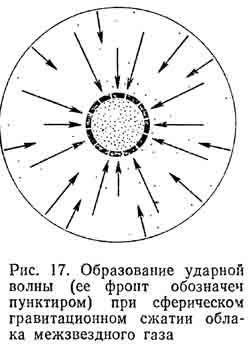
Az interstelláris közeg dinamikájának egyik fontos esete az 1. ábrán látható. 17 - csepp csillagközi gáz saját hatása alatt a felhő közepére. Ez az esés egy sűrítési régiót hoz létre a felhő közepén, amelyet a középpontból szétszórt gömbös lökéshullám vesz körül. Nyilvánvaló, hogy még itt is nagyon erős anyagösszehúzódás van, de már egy igazi objektumban, vagyis ez a jelenség nagyon lehetséges a csillagok kialakulásában.
Shock wave formation
A csillagközi gázdinamika harmadik jellemzője a mágneses mezők alapvető szerepe. Tekintsük ezt a funkciót az olvasó számára az iskolai fizika tanfolyamában ismert példában. Ha egy mágneses mezőt egy vezető vezet át, akkor elektromos áramot indukál, ami mágneses mezőt hoz létre. E mezők kölcsönhatásának eredményeként létezik olyan erő, amely gátolja a vezető elmozdulását (a Lenz-szabályt). Ha a vezető elektromos ellenállása nagy, az indukált áramok és a mágneses mezők gyengék, és a vezetők könnyen mozognak egy mágneses mezőben. De ha a vezetõ elektromos ellenállása nagyon kicsi, akkor meglehetõsen erõs indukált áramok keletkeznek, és a vezetõ elmozdulásával szembeni ellenállóképesség lényegesen megemelkedik - a vezetõ "elakad". Például ismeretes, hogy egy szupravezetőt nem lehet egy mágneses mező által elfoglalt területre nyomni. (Emlékezzünk rá, hogy ha egy vezeték egy mágneses mező mentén mozog, akkor egyáltalán nincs áram, és nincs ellenállás egy ilyen mozgással.)
És most vissza a csillagközi gázhoz. Itt, mint tudjuk, sok szabad elektron van, ezért az interstelláris gáz elektromos vezetőképessége elég magas (még jobb, mint a réz elektromos vezetőképessége). Ezért az ilyen gáznak az interstelláris mágneses mezőn keresztüli mozgása meglehetősen hasonlítható ahhoz, hogy ugyanabban a mezőben egy jó fémkábel eltolódjon. Itt is figyelembe kell vennünk, hogy a csillagközi felhők hatalmas dimenziói nagyon érzékelhetővé teszik a mágneses mezőben való fékezés hatását.
Így az interstelláris mágneses mezőnek gátolnia kell a csillagközi felhők mozgását a mező irányába, és nem zavarja a mozgásukat a mezőn. Várható, hogy a csillagközi gázáramok elsősorban a mágneses erővonalak mentén vannak irányítva. Ezt a következtetést megerősítik megfigyelések: valójában a gáz a galaxis síkjával párhuzamosan mozog, és a mágneses mező közel azonos irányba mutat.
Azonban, ha az interstelláris mágneses mező gyenge, így már nem állíthatja le a gáz mozgását az erővonalakon, akkor a gáz elindul önmagával és a mágneses mezővel. Más szavakkal, a mozgó gázáramok mágneses vonalakat vonzanak mögöttük, húzva és csavarva őket. Ebben az esetben azt mondják, hogy az erő mágneses vonalai "fagynak be" a csillagközi gázba (vagy a csillagközi gáz "ragasztva" a mágneses erővonalakhoz).
A mágneses mező erővonalainak fogalmának meghatározásából ismert, hogy a H mágneses mező (vagy a B mágneses indukció) intenzitása arányos az egy területen átmenő erővonalak számával. Amikor a gázmozgás vonja és "összefonódik" az erő mágneses vonalaihoz, ezáltal növeli a H (és B) értéket. Elmondható, hogy itt a gáz kinetikus energiája mágneses energiává alakul. A mágneses tér növekedése a gáz mozgása alatt felfüggesztésre kerül, amikor ezek az energiák ugyanolyan sorrendben fordulnak elő: pv2 / 2
B2 / 8n (itt p a gáz sűrűsége, bal oldali kinetikus energia sűrűsége és a mágneses energia sűrűsége jobb oldalon). A mágneses mező javítása különösen a fent említett sűrűsugaraknál észrevehető. A sűrűség növekedését a terület "befagyott" elve alapján a B értékének arányos növekedése kísérte.
A negyedik jellemző a csillagközi gáz dinamika megléte ionizációs frontok - dvi-mozgó határok között, a zónák és a régiók HII HI. Úgy tűnik, hogy a H II zónákban a gáznyomás általában sokkal nagyobb, mint a gáznyomás a HI-régiókban. Tény, hogy figyelembe véve a termodinamika közötti csillag, azt találtuk, hogy egy kétkomponensű rendszer, amely a felhők és mezhoblach-sósav középnyomású (vagy pontosabban, a termék nT) nem nagyobb, mint 3 • március 10 K / cm 3 Másrészt , a H II zónában, ahol T = 10 4 K, ez az érték a protonok és elektronok koncentrációjának "standard" értékénél (n
m -3), és nagyobb koncentrációknál a különbség még észrevehetőbb.
Így a HII zónáknak ki kell terjeszteniük a környező teret. De a gáz tágulása sűrűség zónán belül csökken, kevesebb rekombináció nemzetek és ennek eredményeként ebben a zónában része a „nem használt” ionizáló sugárzás. Átmennek a H II zóna kezdeti tömegének határán és ionizálják az új hidrogénatomokat. Így az egész pro-folyamat egyik tagja nem csak a habosító adalék anyag maga HII régió, hanem a gyorsabb promóciós régiók közötti határokat ionizált és nem ionizáló-vannogo hidrogén - Zóna HII növekszik mind az idő-intézkedések és nagyságát a tömegét .
A H II zóna határainak ilyen mozgását az ionizációs front mozgásnak nevezik, amelynek elmozdulási sebességét összehasonlíthatjuk a hang sebességével a HI régióban. Ha az ionizációs front sebessége nagyobb, mint a hang sebességének ugyanabban a gázban, akkor az R-típusú frontról beszélünk. Itt, amikor ezen a fronton halad át, a gáz ionizált és kondenzált.
Ezzel szemben, ha az elülső sebesség kisebb, mint a megfelelő hangsebesség, akkor az ionizációs fronton (D-típusú front) a koncentráció csökken. Ennek a csökkentésnek a biztosítása érdekében a D-típusú front gyakran "eljuttatja" a lökéshullámot, amely előtte "nyomja" a gázot a HI régióban.
Amint egy új forró csillag keletkezik a HI régióban, először egy kis HII zónát hoz létre, amely R-típusú ionizációs frontként gyorsan bővül. Ezután csökken a H II kiterjesztett zóna sebessége, egy lökéshullámot továbbítanak, majd egy D típusú ionizációs frontot rövid távolságra.
A csillagközi gázdinamika tulajdonságainak ismerete feltétlenül szükséges ahhoz, hogy megértsük a csillagok kondenzációját az interstelláris közegtől - ez a kondenzáció nem más, mint a csillagközi gáz mozgása. És ahogy az alábbiakban is látni fogjuk, az csillagközi gázdinamika jellemzői a csillagkép alakulásának különböző aspektusaiban jelennek meg.