A matematika oktatója a planimetria további tételeiről
H és ezt az oldalt tartalmaz a tétel a sík geometria matematikai oktató lehet használni előállítására alkalmas diákok egy komoly vizsgálat: verseny vagy vizsga a Moszkvai Állami Egyetemen (előkészületben Mekhmat, WFC), az olimpia a magasabb School of Economics, az olimpia Akadémia Pénzügyi és a MIPT-ben. Ezeknek a tényeknek a megismerése nagyszerű lehetőségeket kínál az oktató számára a versenyképes feladatok összeállításához. Inkább „legyőzte” néhány ilyen elmélet a számok vagy kiegészítheti elemek egyszerű kapcsolatot más matematikai objektumok, és az eredmény elég tisztességes Diákolimpia feladat. Számos tulajdonság van jelen az erős iskolai tankönyvekben, mint bizonyítási problémák, és nem szerepelnek kifejezetten a bekezdések fejléceiben és szakaszaiban. Megpróbáltam kijavítani ezt a hiányosságot.
A matematika hatalmas tárgy, és a tények száma, amelyeket teoretikusként lehet kiemelni, végtelen. A matematika oktató nem tudja fizikailag tudni és mindent emlékezni. Ezért a geometriai objektumok közötti néhány bonyolult kölcsönhatás ismét megnyílik a tanárnak. Ha mindegyiket egy oldalon egy időben összegyűjtjük, fizikailag lehetetlen. Ezért fokozatosan kitöltöm az oldalt, mivel a tételeket az óráimban használják.
Azt tanácsolom, hogy a matematika tanárai kezdjenek óvatosabban használni további referenciaanyagok használatát, mivel a legtöbb ilyen tényről az iskolás gyerekek nem tudják.
A matematika oktatója a geometriai alakok tulajdonságairól
1)
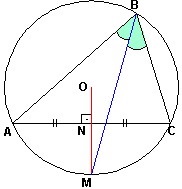
2)
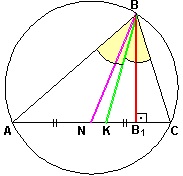
3)
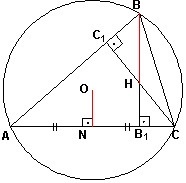
4)
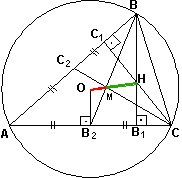
5)
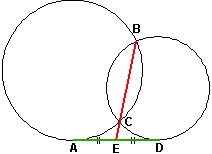
6)
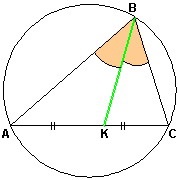
Vagyis a következő egyenlőség tartja
7)
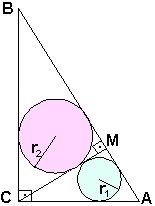
8)
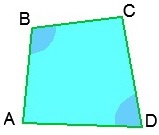
, ahol x a négyszög két ellentétes szögének összege. Ha ez a négyszög egy körbe van írva, akkor a képlet szintén a következő alakú:
és a Brahmagupta-formula
9) Ha a négyszöget körülírták (vagyis a kört be van írva), akkor a négyszög területét a következő képlet adja meg:
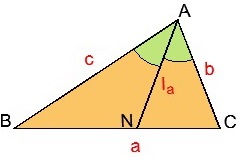
10)
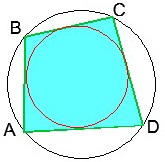
11)
Egy tapasztalt oktatónak, hogy ne veszítse el a képesítést, javaslom, hogy rendszeresen ellenőrizze az olimpiai változatokat, függetlenül a jelenlegi hallgatók összetételétől. Először is, hogy fenntartsuk a megfelelő fejlettségi szintet. Nézd meg a referenciakönyveket és enciklopédiákat. Bővítse a látószögét és javítsa! Ehhez az oldal elkészült!
A geometriai tények további ismereteinek jelenlétében a matematika oktató nagy segítséget fog nyújtani a hallgatóknak a gyors megoldások keresésében. Például ilyen segítséget kaphatok tőlem Stroginóban. A jövőben, amikor sürgősen dolgozik a feladatokkal, ez a C4-es probléma megoldásának időtartamát csökkenti az USE matematikában. A vizsga, meg lehet oldani a problémát bármilyen megfelelő módon, még az alapok felhasználása és tulajdonságai kívül az iskolai tananyag (beleértve az alkalmazott magasabb matematika).
Nagy tisztelettel, Kolpakov AN
Képzett matematikai oktató. Strogino. m. Shchukinskaya. Felkészülés bármilyen vizsgálatra, valamint az olympiadsokra.
Köszönöm. Az oldal anyagai színesnek vannak tervezve és rendelkezésre állnak, gyakran háztartási feladatok megoldásakor. Sajnos egy másik városban lakom, és nincs lehetőség egy oktató bérlésére. Az iskolában a lehető legkevesebbet adják, így számomra sok ilyen tétel nem ismerős.
Véletlenül megbotlott a helyszínen. Nagyon szép, világos, fehér. Elmentem a kérésre - a magasságok metszéspontján.
Ha bizonyíték lenne, sokkal könnyebb lenne.