A labda mennyisége
Chebyshev mechanizmusa A projekt összegyűjti a nagy orosz matematikus - Papnutii Lvovich Chebyshev (1821-1894) által létrehozott mechanikát.
Mathesis Odessza kiadó "Mathesis" 1904 és 1925 között meglepően érdekes könyveket készített. Néhányan klasszikusokká váltak, néhányat elfelejtettek. Egyesíti őket, hogy mindegyikük ritkaság.
V.O.F.E.M. A népszerű tudományos folyóirat elektronikus változata, amely az orosz nyelvű irodalom műfajának tendenciáját határozta meg.
Ha a CD-t vagy a DVD-t "égeti" a számítógépeden, az "üres" rögzített része sötétebbnek tűnik, mint a nem használt.
Mi több, a képen látható lemezen. - rögzített információ vagy szabad terület?
A matematika szempontjából mind a CD-, mind a DVD-meghajtó egy gyűrű. A belső kerülete sugara, amely a körön van, amelyen semmit nem írok, 2 centiméter. és a teljes szabványos lemez sugara 6 centiméter. Az információt egy spirális pályán rögzítik, amelyet egy kisebb körből egy nagyobbikra húznak. Mivel az azonos mennyiségű információ a pálya azonos hosszúságának felel meg, az "üresen" rögzített információ mennyisége arányos a gyűrű által elfoglalt területével.
Kezdjük "égetni" a lemezt, mint egy számítógép. Ha a rögzített gyűrű szélessége megegyezik a nem rögzített szélességével, és 2 cm-t tesz ki, akkor láthatja. mennyivel kevesebb a használt rész területe. Ebben az esetben még akkor is, ha a rögzített gyűrű területét hozzáadja a teljes belső körhöz, amelyhez semmi sem íródik, akkor teljes területük még mindig kisebb lesz, mint az "üres" nem rögzített részének területe.
Annak érdekében, hogy az "üres" pontjának pontosan felét elfoglalják, a belső gyűrű szélessége körülbelül 2,5 cm, a külső gyűrű pedig körülbelül 1,5 cm.
Miért keletkezik ilyen hatás?
A síkon a labda egy kör, és ennek megfelelően a kötet a körnek ez a területe. Mint mindenki tudja, a $ R $ sugár körének területe egyenlő $ \ pi R ^ 2 $ értékkel. A gyűrű területének kiszámításához a kihagyatlan kis - $ \ pi \ cdot (R ^ 2 -r ^ 2) $ területét el kell vonni a nagy kör területéről. És mivel minden a sugártól függ, és még a négyzetben is, annál közelebb van a gyűrű a nagyobb sugárnak, annál nagyobb, ugyanolyan szélességű, mint a területhez való hozzájárulás.
Háromdimenziós térünkben a gömb térfogata függ a sugártól, amely a harmadik hatalommal emelkedik. Ez azt jelenti, hogy a vizsgált hatás még hangsúlyosabbá válik: bóA labda nagyobb része a határ közelében koncentrálódik!
Mi több a narancssárga héjban vagy pépben? Az arca egy látszólag nem túl vastag réteget vesz fel, de a labda határa mellett helyezkedik el. És a fenti ábrán szereplő mennyisége megegyezik a narancssárga egész ízletes részének térfogatával. Narancs megvásárlása vastag bőrrel, térfogatban alapvetően egy héjat kap.
Nézzétek is
A "Négyzetek és kötetek" rész vázlatai 4
Interaktív puzzle "A pitagorai tétel"
Gyönyörű interaktív bizonyíték a pitagorai tételről.
Négyzetnyi számok
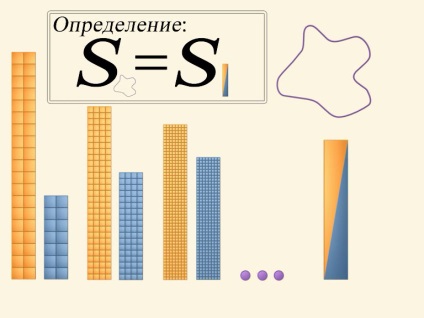
A négyzet négyzet egyenlő az oldalának négyzetével. Könnyű kiszámítani egy olyan területet, amely több négyzetre oszlik. És mi az a terület, amelyet egy tetszőleges görbe határol?
A csúcs formula
Interaktív számítása a sokszög által kijelölt területnek.
A labda mennyisége: Archimedes mérlegel

A gömb legnagyobb körével rendelkező bolygó és a gömb szélességével egyenlő magasságú palack egy és fél gömb; és felülete a gömb egy és fél felének felülete. Archimedes