A csúszó súrlódási együtthatók értéke és a gördülő súrlódás egyes anyagokra
Annak megállapításához, a tapadási súrlódási együttható tribométer készülék segítségével, amely lehetővé teszi, hogy számít a dőlésszög a mozgó sík 1, tekintettel a vízszintes síkban 2. Szög tangense egyenlő a tapadási súrlódási együttható, amellyel a 3 test, hozott egy síkban 1 elkezd mozogni. A szöget a transport-4 mérik.
A súrlódási kinematikai együttható meghatározásához telepítésre van szükség, amelynek eszköze könnyen megérthető az ábrán (lásd a 2.3 ábrát). A 2 test a 1 sík mentén mozog a 4 fészek által dobott feszítés hatására. A feszítőerőt a terhelés 3 súlyának megváltoztatásával szabályozzuk.
A súrlódási erő egyenlő a csésze súlyával a terheléssel, amelynél a 2 test egyenletesen csúszik a felszín fölött -1
ahol m a csésze tömege a terheléssel,
(ksk a csúszó súrlódás kinematikai együtthatója,
mm a test-2 tömege,
- a gravitáció gyorsulása.
A (2.7) egyenlet megoldása a kc értékhez képest. kapunk
Loading Tepo-2, tudomásul vesszük, hogy a mozgás egy nagyobb tömegű túlterhelés kivetett kupa-3. De az arány mindig állandó, egyenlő a súrlódási együtthatóval.
TELJESÍTMÉNYI RENDELÉS
1. Állítsa be az egyik javasolt testet a tribométeren, lassan emelje fel a 2-es síkot, vegye észre, hogy a test elkezd csúszni,
2. Futtassa a mérést többször, majd írja le az adatokat egy korábban készített 2.2 táblázatba.
3. Fordítsa el a testet egy másik síkra, és ismételje meg a kísérletet.
4. Következtetés levonása.
5. Az ilyen méréseket a tanár által javasolt más mintákkal kell elvégezni.
6. Határozza meg a pihentetési súrlódási tényezőt az azonos átmérőjű hengeres minták esetében, amelyek különböző anyagokból készültek (2.4.)
7. Hasonlítsa össze a csúszó súrlódás és a gördülő súrlódási együtthatókat azonos párosítási felületek esetén.
8. Hasonlítsa össze a pihenés és a mozgás súrlódási tényezőit azonos pár dörzsölő felületekre.
A sztatikus súrlódási együttható meghatározása
1. Formálja a súrlódási erő függését a normálnyomás erejéről.
2. A kapott függőségből (grafikon) határozzuk meg a súrlódási tényező középértékét.
1. Mi a súrlódás ereje? Milyen a száraz súrlódás ereje a test felszínére irányul?
2. Mi az úgynevezett pihenés súrlódása, csúszó súrlódás, gördülő súrlódás?
3. Milyen mértékben függ a súrlódási tényező?
4. Milyen típusú súrlódást tudsz?
5. Mi az a mértékegység a súrlódási tényező mérésére?
6. Mi a súrlódási együttható értéke a mezőgazdaságban?
7. Adjon példákat a súrlódási erők használatára a mezőgazdasági gépek üzemeltetésében.
8. Milyen súrlódást nevezünk belsőnek?
9. Mi határozza meg a belső súrlódás erejét?
LABORATÓI MUNKA №3
A FORGALMAZÁS DINAMIKÁJA ALAPJOGÁNAK ELLENŐRZÉSE
A HATÁROKON ÁTTEKINTŐ PENDULUM ALKALMAZÁSÁRA VONATKOZÓ KÖTELEZETTSÉG
A dokumentum célja a rotációs mozgás dinamikájának alapvető jogának megvalósíthatósága.
Eszközök és tartozékok: Oberbek inga, terheléskészlet, stopper, féknyereg, vonalzó.
A alaptörvénye dinamikáját forgómozgást egy merev test teljesen a következőképpen hangzik: A forgatónyomaték a ható erő test a termék a tehetetlenségi nyomatéka a test szöggyorsulással adódik át a testet, és meg van írva a következő:
hol van a forgó erő nyomatéka,
- a test tehetetlenségi nyomatéka,
- a test szögletes gyorsulása.
A tehetetlenségi nyomaték intézkedés a tehetetlenségi test és általában egyenlő a tehetetlenségi nyomaték alkotó anyag pont
- az anyagpont sorozatszáma, = 1,2,3, ......
Az anyag adott forgástengelyhez viszonyított tehetetlenségi nyomatéka megegyezik e pont tömegével az e ponttól a forgástengelyig tartó távolság négyzetével
itt m egy anyagpont tömege,
r az anyagponttól a forgástengelyig terjedő távolság.
Az erő pillanat olyan vektor-mennyiség, amelynek modulusa megegyezik a karon lévő erő termékeivel
itt M az erő pillanat,
F a testen ható erő,
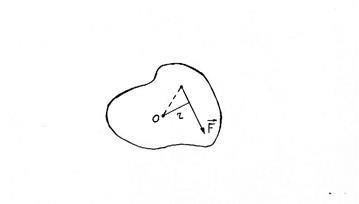
Az erő pillanatát kétféle módon lehet megváltoztatni: az erő megváltoztatása, vagy az erő váltakozása ugyanolyan erővel.
Munkánkban megváltoztatjuk a cselekvő erő nagyságát, változatlanul hagyva az erőszakot.
Ha a forgó erő nyomatékát az inga állandó tehetetlenségi nyomatékában megváltoztatják, a szögsebesség változik. De a forgó erő nyomatékának aránya a szögsebességhez állandó érték lesz, amely egyenlő az inga tehetetlenségi nyomatékával.
A munkában meg kell vizsgálni a nyilatkozat helyességét.
Keresztalakú inga (lásd. Ábra. 3.2.) Olyan lemez, amelynek megerősített -1 rajta szögben 90 0 egymáshoz négy hosszú rúd 2, amely lehet mozgatni a tömeges m0 terhelések -3 egyes. Az 1 blokk lehet tekercselni -4 menet, a szabad vége, amely hordozza az tömeg terhelés -5 m.
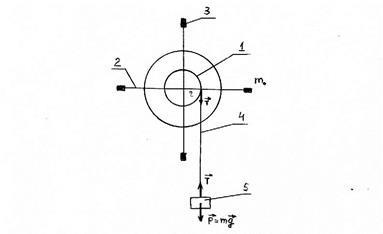
A szál feszültsége miatt a felfüggesztett tömeg gravitációja hatására az inga mozgásban van, azaz a menet húzóereje a forgó inga ereje lesz, és ennek az erőnek a válla lesz a tárcsa sugara. A terhelés mozgása egyenes vonalú, egyenletesen felgyorsulva az a gyorsulással, amelyet az egyenletesen gyorsított transzlációs mozgás egyenletéből határozhatunk meg a kezdeti sebesség nélkül:
itt h a terhelés csökkenésének magassága,
a a gyorsulás, amellyel a rakomány mozog,
t - a rakomány mozgásának ideje.
A szögsebesség a lineáris viszonyhoz kapcsolódik:
,
A menet feszessége megtalálható a rakománymozgás egyenletéből:
itt g a gravitáció gyorsulása (g = 9,8 m / s 2).
A forgó erő nyomatékát az alábbi egyenlettel fejezzük ki:
Itt r az a lemez sugara, amelyen a szál fel van csavarva (lásd a 3.2. Ábrát).
Ha a (3.1) egyenletből a (3.3.) Egyenlet értékét helyettesítjük, akkor a következőket kapjuk:
TELJESÍTMÉNYI RENDELÉS
- Mérje meg a tárcsa átmérőjét egy féknyeréssel.
- A terhelést egy bizonyos magasságra emelve hagyja szabadon engedni, az inga forgatásával.
- Mérje meg a terhelés idejét.
- Jegyezze fel a mérési eredményeket a táblázatban.
A mérési eredmények rögzítésének táblázata
- Számítsa ki az inga gyorsulását a (3.2.) Egyenlet segítségével
- Számítsa ki a forgató erő nyomatékát a (3.4.) Egyenletből.
- megtalálja a hozzáállást.
- Számítsa ki a hibákat.
- Legyen egy függvény grafikonja b = f (m)
- A b = f (m) függvény grafikonjának segítségével határozzuk meg a súrlódási erők pillanatát.
- Méréseket végezhet az áruk forgási tengelyének távolsága megváltoztatásával. Hasonlítsa össze az eredményeket.
- Formázza meg a rotációs mozgás dinamikájának alapjogát.
- Mi az anyagi pont tehetetlensége?
- Mi az úgynevezett hatalom pillanata?
- Mi az anyagi momentum lendülete?
- Mi az impulzus pillanatnyi mértékegysége az SI rendszerben?
- Mi nevezik a hatalom vállának?
- Mi az impulzus pillanatnyi mértékegysége az SI rendszerben?
- Mi az egység egy anyagpont szögletes lendületeinek mérésére az SI rendszerben?
- Mi az egy egység egy erő impulzusának mérésére az SI rendszerben?
- Hogyan határozható meg a szilárd test tehetetlenségi nyoma?
LABORATÓI MUNKA №4