Példa a súlypont és a tehetetlenségi nyomaték kiszámítására

Felhívjuk a figyelmet arra, hogy ezen az oldalon egy online szolgáltatás áll rendelkezésre az összetett szakaszok gravitációs középpontjának és a tehetetlenségi nyomatékának kiszámítására, amely gördülő profilokból (I-gerenda, sarok stb.) És egyszerű számokból áll.

Az épületszerkezetek elemeinek kiszámításánál gyakran el kell végezni az elemi geometriai alakok (téglalap, kör stb.) És gördülő profilok geometriai jellemzőit. Nézzük részletesen a számítási példát.

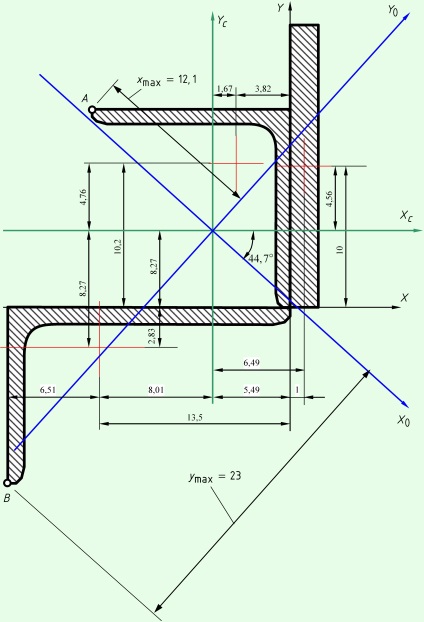
Meg kell határozni az összetett rész geometriai jellemzőit (ábra), amely 20 / 12,5 / 1,2 sarokból, 14/1 sarkából és 20x2 cm téglalapból áll.

Az egyes profilok belső jellemzőinek meghatározása - az alkotóelemek

A gördülő profilok sajátosságait a választék határozza meg.

Az egyenlőtlen szög esetében: 20 / 12,5 / 1,2:

- a sarok magassága és szélessége h = 20 cm, b = 12,5 cm;

- $ A $ = 37,9 cm2 terület;

- saját axiális nyomatékai $$ = 1570 cm 4. $$ = 482 cm 4;

- saját centrifugális momentuma tehetetlensége $> $ = 505 cm 4;

- a súlypont koordinátái $$ = 2.83 cm, $$ = 6.51 cm.

Az egyenlő szögben 14/1:

- a sarok magassága és szélessége h = b = 14 cm;

- terület $ A $ = 27,3 cm 2;

- saját axiális nyomatéka $$ = $$ = 512 cm 4;

- saját centrifugális tehetetlenségi nyomatéka $> $ = 301 cm 4;

- a súlypont koordinátái $$ = $$ = 3,82 cm.

A 20x2cm téglalap esetében:

- a téglalap magassága és szélessége h = 20 cm, b = 2 cm;

- $ A $ = 20 ∙ 2 = 40 cm 2 terület;

- saját centrifugális momentum tehetetlensége $> $ = 0, mivel a profilnak van egy szimmetriatengelye.

A jármű tömegközéppontjának meghatározása

A teljes terület teljes területe A = 37,9 + 27,3 + 40 = 105 cm 2.

A $ X $ és $ Y $ segédtengelyeket rajzoljuk, és meghatározzuk a szakasz súlypontját a számukra:

Ebben az esetben a vegyes feladatok súlypontjainak koordinátáiban figyelembe kell venni a jelet. Elhúzzuk a tengelyeket, amelyek áthaladnak a súlyponton - az $ Xc $ és a $ $ középtengelyein.

A tehetetlenség központi nyomatékainak meghatározása

A keresztmetszet axiális és centrifugális tehetetlenségi nyomatékait a párhuzamos tengelyek közötti átmenet képletei határozzák meg. Ebből a célból a rajzon található és megmutatjuk a teljes szelvény központi tengelyei és az egyes számok saját tengelyei közötti távolságokat.

= $ 505 + (- 8,01) \ cdot (- 8,27) \ cdot 37,9 - 301 + 1,67 \ cdot 4,76 \ cdot 27,3 + 0 + 6,49 \ cdot 4,56 \ cdot 40 = 4120 $ cm 4.

Ugyanakkor a feladatok "szükségszerűen figyelembe veszik a számokat a szóban forgó tengelyekhez viszonyítva. Így, a meghatározó tehetetlenségi nyomaték a képlet $$ helyettesítheti saját tehetetlenségi nyomatéka egyenlő konzol egy tengely körül, amely párhuzamos a tengellyel $$ ebben választék tengelyen $ Y $, és fordítva.

A fő tengelyek helyzetének és a tehetetlenségi nyomaték meghatározásának meghatározása

A fő tengelyek forgási szöge azokhoz a tengelyekhez képest, amelyeknél a tehetetlenségi nyomaték ismeretes, a következő képlet

Ha $ \ alpha> 0 $, akkor a fő tengelyeket az óramutató járásával ellentétes irányba rajzolja, és fordítva.

A tehetetlenség fő pillanatait ilyen módon határozzák meg

= $ 6360 \ cdot (- 44,7 ^ \ circ) + 6280 \ cdot (- 44,7 ^ \ circ) - 4120 \ cdot \ sin (- 2 \ cdot 44,7 ^ \ circ) = 10430 $ 4 cm .

= $ 6280 \ cdot (- 44,7 ^ \ circ) + 6360 \ cdot (- 44,7 ^ \ circ) + 4120 \ cdot \ sin (- 2 \ cdot 44,7 ^ \ circ) = 2210 cm $ 4 .

A tehetetlenségi centrifugális nyomaték a fő tengelyekhez képest nulla.

A tehetetlenségi ráta. Az ellenállás pillanatai

A metszet tehetetlensége

A szakasz-ellenállás pillanatai a központi tengelyekhez viszonyítva kerülnek meghatározásra. Ehhez meg kell határozni a $> $ és $> $ távolságokat a fő tengelyek legtávolabbi pontjaihoz. Először meg kell állapítanunk a rajzokon, hogy mely pontok a legtávolabbiak. Esetünkben ezek a $ A $ és $ B $ pontok (ábra). A kívánt távolságokat úgy lehet meghatározni, hogy ezeknek a pontoknak a koordinátái középpontban (a tengelyekhez nem térnek vissza).

$ \ \ \ \ \ \ \ left \ alpha \ right \ left \ alpha \ right \ left \

$ \ cdot \ cos \ left \ alpha \ right \ cdot \ sin \ left (\ alpha \ jobb) $

X A = -8,53 cm, Y = 8,57 cm

X B = - 14,5 cm Y B = - 18 cm

x max = - 12,1 cm y max = - 23 cm