A tangens portfólió struktúrájának megkeresése - pénzügy

1. Az érintő portfolió struktúrájának megkeresése.

2. A tőke elosztása az érintő portfólió és a kockázatmentes eszköz között az egyedi kockázati étvágy függvényében.

A szétválasztási tételként ismert a képesség, hogy külön-külön megoldja a portfólió kockázati részének és a portfólió egészének optimalizálását.

Ugyanezek a megállapítások és az eredményeket egy formális matematikai megoldás Tobin probléma adott, például a [3 str.109-113] (minősített esetekben a felvett és nélkülük). Amellett, hogy a klasszikus módszerek formai megoldások Tobin feladatok léteznek „speciális” alkalmazásán alapuló az elválasztás tétel; az érintő portfólió kezdeti felfedezéséről. Például, lehet használni a módszert már említett kritikus vonalak vagy leírt [4 str.253-256] EGP módszer, elemzi Elton alkotók, és Gruber Padberg (módszer a tulajdonság az érintő portfolió maximális hajlásszöge az egyenes összekötő vonal pont a megfelelő kockázatmentes hozam).

A Tobin eredményeinek makrogazdasági jelentősége a pénzkereslet modellezése, amikor a kockázatos eszközök jövedelmezősége megváltozik.

Bár a feltételezés a lehetőségét, hogy egy tisztán Tobin riskless beruházások a gyakorlatban nem feltétlenül kivitelezhető megoldás, a problémát a Tobin slaboriskovyh eszközök közel van az elméleti, és ezért a gyakorlati haszna a [3, p.112].

2.4. A CAPM modell és annak generalizálása

Az elején a 60-as évek inas Markowitz William Sharpe javasolták ún egytényezős modell a piacon fővárosok, ami megjelent az első alkalommal vált ismertté később az „alfa” és „béta” - a jellemzői a részvények. Az egyfaktoros modell alapján a Sharpe egy egyszerűsített módszert javasolt az optimális portfólió kiválasztására, ami csökkentette a kvadratikus optimalizálás problémáját lineáris optimalizálással. A legegyszerűbb esetekben kis dimenziók esetén ez a probléma gyakorlatilag "kézzel" megoldható. Ez az egyszerűsítés a portfólió optimalizálási technikákat alkalmazta a gyakorlatban. A 70-es években. a programozás fejlesztése, valamint az egyes értékpapírok alfa és béta mutatóinak és a piaci jövedelmezőségi index egészének értékelésére szolgáló statisztikai technikák fejlesztése az első szoftvercsomagok megjelenéséhez vezetett a portfoliókezelési problémák megoldásához.

A Sharpe eredetileg a kezdeti adatok megszerzésének egyszerűsítését célozta meg (elsősorban az értékpapírok hozamai közötti kovariancia), ami a Markowitz portfóliójának optimalizálásának problémájához szükséges. Ebből a célból egy tényezõs modellt alkalmaztak a hosszú távú kockázati biztosíték hozamának függvényében a tényezõre - az állományok piaci kapitalizációjának súlyozott átlaga:

hol van a piacon forgalomban lévő összes értékpapír száma,

- a teljes piaci kapitalizáció részesedése és a n. értékpapír hozama.

Az n-edik biztonsági hozam egytényezős modellje a legkisebb négyzetek módszerével nyert lineáris regressziós függőségként alakul ki:

hol van a regressziós modell elmozdulási együtthatója, amely tükrözi az aktív hozamot - e biztonság további hozama - és a befektetők érdeklődésének mértéke,

- az értékpapírok hozamában bekövetkezett változások érzékenységének együtthatója az átlagos piaci portfólió hozamának változásához viszonyítva,

- a regressziós modell hibája, amely az összes többi tényező hatását tükrözi.

A regressziós függőség azon a feltevésen alapul, hogy az összes értékpapír hozama csak egy tényezőtől függ - és ennek következtében a hibák kölcsönös korrelációjának és a legkisebb négyzetek módszerének algoritmusából következik, hogy

ahol - RMS, az n-edik biztosíték hozama és az átlagos piaci portfólió,

- korrelációs együtthatót a második biztosíték hozama és az átlagos piaci portfólió hozama között.

Ha tudja, hogy az összes kockázati tényező az állomány eszközök (és arra a következtetésre, hogy az értékelést figyelembe véve a láthatóságát a gyakorlatban a tőzsdén jött elég gyorsan), akkor a kovariancia hozamok értékpapírok és azok varianciáját lehet kiszámítani a szabályokat valószínűségszámítás, hogy (2.12):

Ezek a szabályok könnyen általánosíthatók a részvények által képviselt kockázatos értékpapírokból álló portfolió esetében:

A portfolió kockázatát az alábbiak határozzák meg:

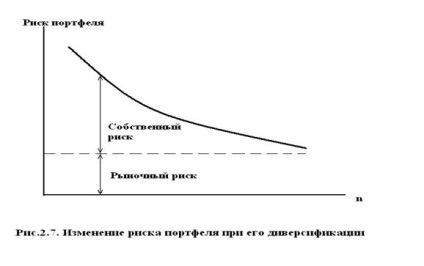
Az első (2.20) kifejezés a piaci (szisztematikus, nem diverzifikálható) kockázatot jellemzi. és a második - saját portfoliókockázat, amelyet a 2.7. ábra szerint diverzifikálva lehet csökkenteni.

De az igazán jelentős tudományos és gyakorlati jelentősége a regresszió közelítés formájában (2.12) és (2.13) alkalmazásával nyert a Tobin-eredményeket szimulációk hosszú távú eszköz árak a tőzsdén.

1964 óta vannak olyan munkák, Sharpe, Lintner, Mossina, kinyitotta a következő fázisban a befektetési elmélet kapcsolódó úgynevezett tőkepiaci árfolyamok modellje, vagy CAPM (Capital Asset Pricing Model). Az ezen iratokban elért eredmények a Markowitz kezdeti feltevésein alapulnak (lásd a 2.2. Szakaszt), kiegészítve a következőkkel:

1. Minden befektető számára a befektetési idő azonos.

2. Az információ szabadon és azonnal elérhető minden befektető számára.

3. A befektetőknek homogén várakozásai vannak, azaz ugyanúgy értékelik a jövőbeni hozamokat, az értékpapírok hozamának kockázatát és kovarianciáját.

4. A kockázatmentes kamatláb minden befektető esetében megegyezik

Az összes kezdeti feltételezés együttesen az úgynevezett tökéletes értékpapírpiacot írja le, amelyre nincsenek olyan tényezők, amelyek gátolják a befektetést. Van egy másik helyzetben carm, ami általában egy A tétel következményeként az osztály: egyensúly, egyes értékpapírok nem nulla részesedése az érintő portfolió, és szerkezetét érintő portfolió követi a piaci portfólió struktúrája összhangban a gazdálkodó kapitalizációja értékpapírok. A magyarázat a következő érv: ha az érintő portfolió a beruházó nem tartalmazza a papír, ami azt jelenti, hogy ő próbál eladni az összes (a befektetők lesz hasonló szerkezetűek kockázati összetevő portfóliója), míg a piaci árfolyam a papír nyomására túlkínálat fog esni és a várható hozam, illetve növekszik - mindaddig, amíg az ár nem lesz egyensúly, ugyanakkor az a tangens portfolió - nullától eltérő. Ellentétes események akkor fordulnak elő, amikor a befektetők egyidejűleg megpróbálják növelni bizonyos papírok részesedését a befektetés kockázatos részében.

A legutóbbi kimutatás és a (2.11.) Alapján a befektető pénzügyi erőforrásaihoz viszonyított várható megtérülés kifejezését írhatjuk ki egy piaci egyensúlyi állapotban:

ahol - mint korábban - az átlagos piaci (tangenciális) portfolió nyereségessége és kockázata,

- a kockázatmentes eszközök jövedelmezőségét

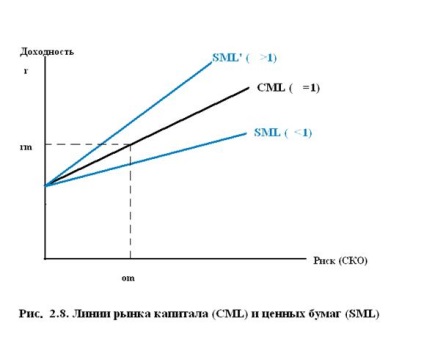
(2.22) leírja a hatékony Tobin frontot (2.8. Ábra), és a Tőkepiaci vonalnak (CML) nevezték. Ebben az esetben a mennyiség

egyenlő a CML dőlésszögének az y-tengelyhez viszonyított tangensével, és tükrözi a jövedelmezőség növekedését a növekvő egységenkénti kockázattal, i.e. a piaci befektetések kockázatának marginális jövedelmezősége kockázatos és kockázatmentes eszközök jelenlétében. Mivel a CML egy konkrét Markovitz frontra vonatkozik, az érintő meredekség érintőjét a kifejezésen keresztül lehet kifejezni. leírva a front Markowitz. Ezt a kifejezést a [Gr] -ben kaptuk, és a következő alakú:

,

amennyiben azok a portfólió bármely értékpapírjához kapcsolódnak,

- a biztosíték hozamának korrelációs koefficiensét és a portfólió egészét.

Az utolsó két kifejezés megfelelő részeinek megegyezésével az optimális portfólióban bármelyik biztonsági érték várható megtérülésére vonatkozó kifejezést kaphat:

amelyet az Equity Market Line (SML) egyenletnek neveznek és a (2.13) ponttól függően, az együtthatóval újraírható:

A különbséget a piaci portfólió nem differenciált kockázatának a prémiumnak nevezik, a különbség pedig a különálló kockázati eszköz birtoklásának kockázata, míg a béta minden egyes értékpapír hozzájárulását a piaci portfólió kockázatához mutatja.

A CML és SML kifejezéseinek összehasonlítása azt mutatja, hogy ezek a vonalak a síkon csak akkor esnek egybe, amikor. Ha az SML vonal magasabb, és - a CML vonal alatt - (2.8. Ábra). Mindenesetre a magas kockázatú eszközöknek arányosan magasabb hozamot kell biztosítaniuk. Így, ha a portfólió hatékony, az egyes részvények várható hozamának és a portfóliókockázatnak járó marginális hozzájárulása közötti kapcsolatnak egyértelműnek kell lennie. A beszélgetés is igaz: ha nincs lineáris kapcsolat, a portfólió nem hatékony.

Az egyenlet SML, akkor lehet meghatározni, hogy túl- vagy átértékelése értékpapír (pl részvények), nem csak a nyereségesség, hanem hogy összehasonlítják a tényleges alakulása és természetesen összhangban az egyensúlyi kockázat ára, ami jelöli. Hagyja, hogy a jövőbeni időszak végén (figyelembe véve az osztalékbevételt) várható részvényárfolyam megegyezzen. A termési kifejezések meghatározása definíció szerint és az SML egyenlet alapján:

,

amelyből a kockázatmentes hozam ismert mértékű diszkontvonala követi, amelyet a kockázati prémium növel:

.

Összefoglalva a fentieket, a CAPM-ot a Markowitz-elmélet makroökonómiai generalizálásaként tekinthetjük, amely lehetővé teszi egy egyensúlyi piac egyensúlyi eszközeinek hozamát és kockázatát. Ugyanakkor fontos, hogy az optimális portfólió kiválasztásakor a befektető ne vegye figyelembe az eszközhöz kapcsolódó "teljes" kockázatot (Markovits kockázat), hanem csak annak nem diverzifikálható részét. Az eszköz kockázatának ez a része szorosan összefügg a teljes piaci kockázat egészével, és mennyiségi szempontból a Sharpe által az egytényezős modellben bevezetett "béta" -szekvenciát képviseli. A többi (nem szisztematikus vagy diverzifikálható kockázat) a megfelelő optimális portfólió kiválasztásával megszűnik. A nyereségesség és a kockázat közötti kapcsolat jellege lineáris kapcsolat. Ha a befektetőknek nincs további információjuk, akkor ugyanazt a részvényportfóliót kell tartaniuk, mint másokkal - értékpapírpiaci portfólió.

1977-ben ezt az elméletet bírálta Richard Roll munkáiban. Roll azzal érvelt, hogy a CAPM-ot el kell utasítani, mert elvben nem teszi lehetővé az empirikus ellenőrzést. A CAPM rendelkezéseinek érvényességére jó néhány kifogás merül fel, a legvitatottabbakat [4] feltételezik:

Tájékoztatás a munkáról: "A hatékony tőkebefektetés elmélete és alkalmazása (az értekezés része)"

Szakasz: Pénzügyek
Szöveges karakterek száma: 34191
Táblázatok száma: 0
Képek száma: 9