A Fibonacci-sorozat kiszámítása

előző ◈ a következő

A Fibonacci-sorozat olyan számsorozat, amelyben minden egymást követő szám megegyezik a két előző szám összegével. Numerikus szekvenciák gyakran megtalálhatók a természetben és a művészetben spirálok és "arany szekció" formájában. A legegyszerűbb módja a Fibonacci-sorozat kiszámításához egy táblázat létrehozása, de ez a módszer nem alkalmazható nagy szekvenciákra. Ha például egy szekvencia 100. tagját szeretné meghatározni, akkor jobb a Binet képlet használata.

Lépések szerkesztése

1. módszer:
Táblázat szerkesztése

Rajzolj egy táblázatot két oszlopgal. A táblázatban szereplő sorok száma függ a megtalált Fibonacci-sorszámok számától.

Például, ha meg akarja találni a sorozatok ötödik számát, rajzolj egy táblázatot öt sorral.
A táblázat használatával nem talál véletlenszámot anélkül, hogy az összes előző számot kiszámolná. Például, ha meg akarja találni a sorozat 100. számát, akkor számolni kell az összes számot: az elsőtől a 99-ig. Ezért a táblázat csak a sorozat első számának megtalálásához alkalmazható.

A bal oldali oszlopban írja be a szekvencia tagok sorszámát. Vagyis írja meg a számokat sorrendben, kezdve egyet.

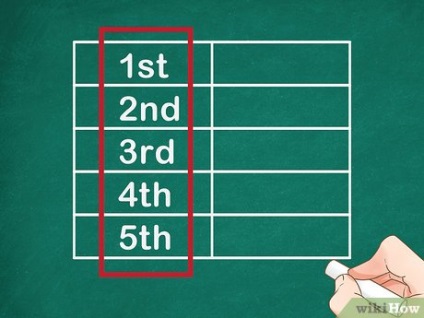
Ezek a számok definiálják a Fibonacci-sorozat tagok sorszámát (számok).
Például, ha meg akarja találni a sorszám ötödik számát, akkor írja be a következő számokat a bal oldali oszlopban: 1, 2, 3, 4, 5. Ez azt jelenti, hogy megtalálja a sorozatok első-ötödik számát.

A jobb oldali oszlop első sorában írj 1-et. Ez a Fibonacci-sorozat első számú tagja.

Ne feledje, hogy a Fibonacci-sorozatot mindig az 1-gyel kezdjük. Ha a sorozat egy másik számmal kezdődik, akkor az összes számot az elsőig hibásan számolta ki.

Az első időtartamra (1) add 0 legyen. A szekvencia második számát kapjuk.

Ne feledje: a Fibonacci-sorozatok számának megtalálásához csak add meg a két előző számot.
Sorozatok létrehozásához ne felejtsd el a 0-at, amely 1 előtt áll (az első tag), tehát 1 + 0 = 1.

Adja hozzá az első (1) és a második (1) tagot. A szekvencia harmadik számát kapjuk.

1 + 1 = 2. A harmadik kifejezés 2.

Adja hozzá a második (1) és a harmadik (2) tagot, hogy megkapja a sorozat negyedik számát.

1 + 2 = 3. A negyedik kifejezés 3.

Hajtsa be a harmadik (2) és a negyedik (3) tagot. A szekvencia ötödik számát kapjuk.

2 + 3 = 5. Az ötödik kifejezés 5.

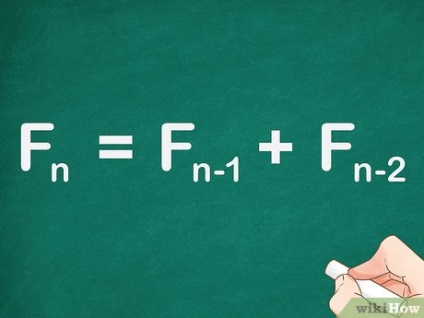
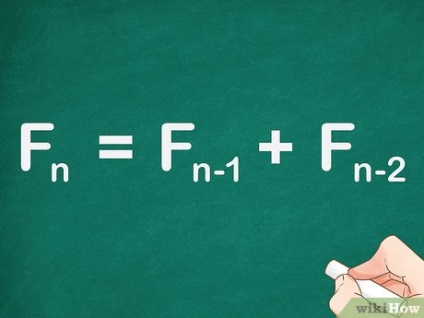
Adja hozzá a két korábbi számot, hogy megtalálja a Fibonacci-sorozatok számát. Ez a módszer a következő képleten alapul: F n = F n - 1 + F n - 2 = F_ + F_>. [1] Ez a képlet nem zárva van, ezért ennek a képletnek a segítségével nem találhatsz semmilyen tagot a szekvencia számának kiszámítása nélkül.

2. módszer 2:
Formula Binet és az arany rész Edit href = Edit

Írja le a képletet: x n> = φ n - (1 - φ) n 5 - (1- \ phi) ^ >>>>. Ebben a képletben x n> a szekvencia kívánt terminusa, n a kifejezés sorszáma, és φ az arany arány. [2]

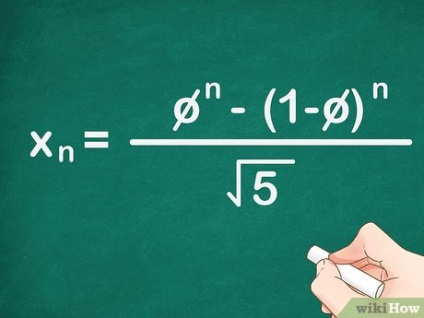
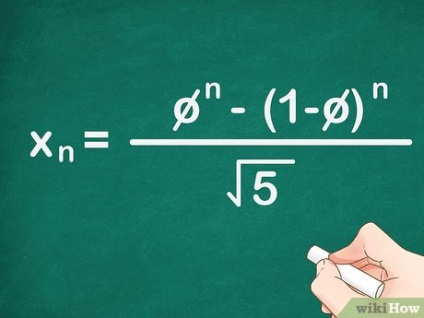
Ez egy zárt formula, így a szekvencia minden tagja megtalálható az összes korábbi szám kiszámítása nélkül.
Ez egy egyszerűsített formula, amely a Binet-képletből származik a Fibonacci-számokhoz. [3]
A képletnek van egy aranyszelvénye (φ), mert a két egymást követő szám Fibonacci-sorozata nagyon hasonló az arany arányhoz. [4]

A képletben helyettesítse a szám sorszámát (n helyett). n a szekvencia bármely kívánt tagjának szekvenciaszáma.

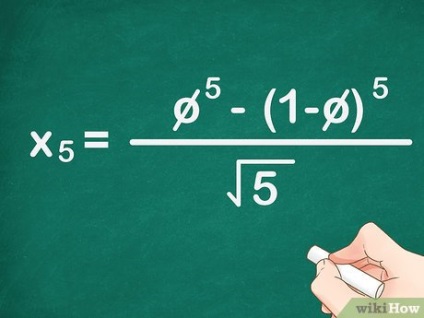
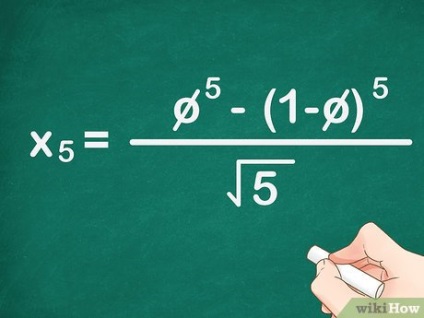
Például, ha meg akarja találni a sorozatok ötödik számát, akkor helyettesíti a képletet az 5 képletben. A képlet a következőképpen van megadva: x 5> = φ 5 - (1 - φ) 5 5 - (1- \ phi) >>>>.

A képletben helyettesíti az aranyat. Az arany szekció megközelítőleg 1,618034; helyettesíti ezt a számot a képletben. [5]

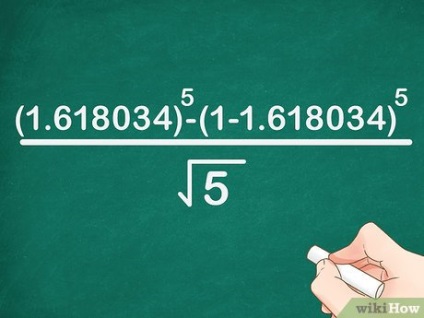
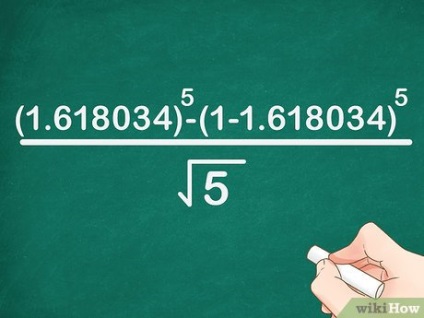
Például, ha meg akarja találni a sorszám ötödik számát, a képlet a következőképpen fog megjelenni: x 5> = (1. 618034) 5 - (1 - 1. 618034) 5 5 - (1-1.618034) ^ >>>>.

Számítsuk ki a kifejezést zárójelben. Ne felejtsük el a matematikai műveletek helyes sorrendjét, amelyben a zárójelben lévő kifejezést először kiszámítjuk: 1 - 1. 618034 = - 0. 618034.

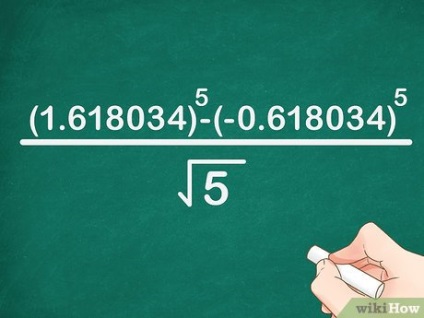
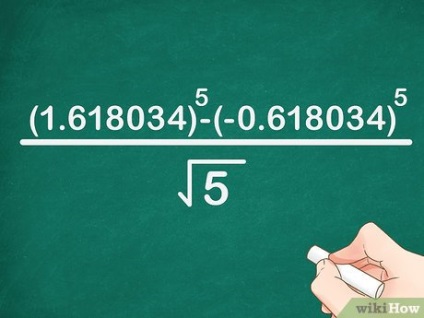
Példánkban a képlet a következőképpen íródott: x 5> = (1. 618034) 5 - (- 0. 618034) 5 5 - (- 0,618034) ^ >>>>.

Emeljük fel a számokat a hatalomra. Emeljük fel a megfelelő teljesítményre két, a számlálóban lévő számot.

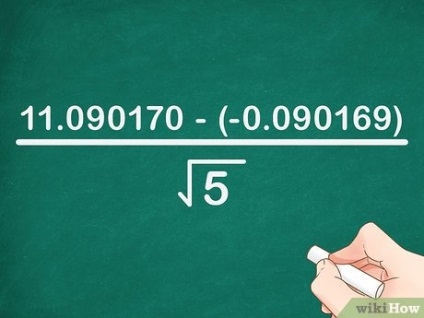
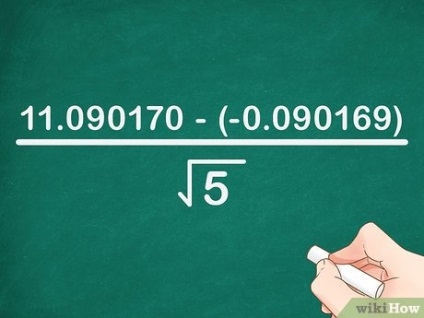
Példánkban: 1. 618034 5 = 11. 090170 = 11.090170>; - 0. 618034 5 = - 0. 090169 = -0,090169>. A képlet a következőképpen fog megírni: x 5 = 11. 090170 - (- 0. 090169) 5 = >>>.

Vonja le a két számot. Mielőtt elkezdi elosztani, vonja le a számlálóban lévő számokat.

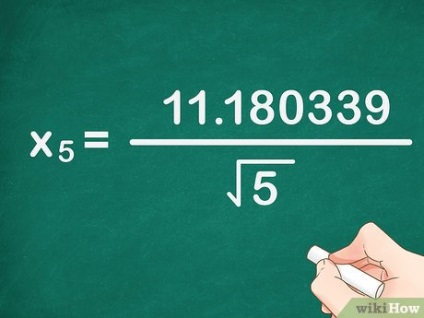
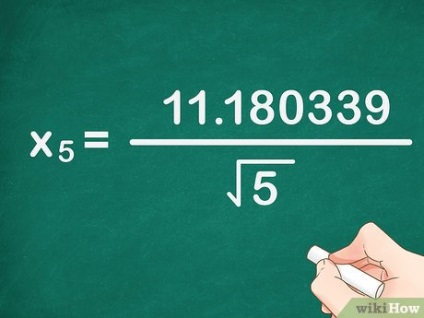
Példánkban: 11. 090170 - (- 0. 090169) = 11. 180339. A képlet a következő: x 5> = 11. 180339 5 >>>.

Osszuk az eredményt az 5 négyzetgyökével. Az 5 négyzetgyök körülbelül 2,236067.

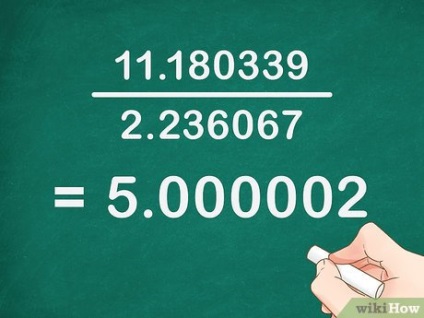
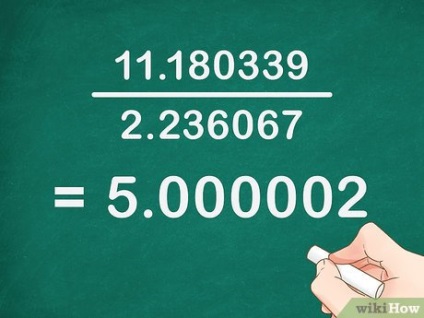
Példánkban: 11. 180339 2. 236067 = 5. 000002> = 5,000002>.

Az eredményt a legközelebbi egész számra kerekítik. Az utolsó eredmény egy tizedes tört, amely közel áll egy egész számhoz. Egy ilyen egész szám a Fibonacci-sorszám.

Ha a számításokban unalmas számokat használ, akkor egész számot kap. A lekerekített számokkal való munka sokkal könnyebb, de ebben az esetben egy tizedes törtet kap. [6]
Példánkban 5,000002 tizedes törtrész van. Fordulj rá a legközelebbi egész számra, és szerezz az ötödik Fibonacci-sorszámot, ami 5.

Kapcsolódó cikkek