Szinusz, koszinusz, érintő, ami olyan, mint a szinusz, a koszinusz és a tangens megtalálása

A matematika egyik szakasza, amellyel a diákok a legnagyobb nehézségekkel szembesülnek, a trigonometria. Ez nem meglepő: a szabadon mester ezen a területen a tudás, ez megköveteli a térbeli gondolkodás, a képesség, hogy szinusz, koszinusz, tangens, kotangensét képletek, hogy egyszerűsítse a kifejezést, hogy képes legyen használható értékének kiszámításakor Pi. Ezen kívül, meg kell tudni használni trigonometry bizonyítani tételek, és ez megköveteli a fejlett matematikai memóriát vagy képes megjeleníteni a bonyolult logikai láncot.

A trigonometria eredete

Ennek a tudománynak az ismerete a szinusz, a koszinusz és a szög meghatározásával kezdődik, de először meg kell értenünk, hogy a trigonometria általában hogyan.

Történelmileg a kutatás fő tárgya a matematikai tudomány e szakasza négyszögletes háromszög volt. A 90 fokos szög jelenléte lehetővé teszi a különféle műveletek elvégzését, amelyek lehetővé teszik a szóban forgó ábra összes paraméterének két oldalról, egy sarokból vagy két szögből és egy oldalról történő meghatározását. A múltban az emberek észrevették ezt a mintát, és aktívan használják az épületek, a hajózás, a csillagászat és a művészet építésében.

Kezdeti szakasz

Kezdetben az emberek beszéltek a szögek és oldalak kapcsolatáról, kizárólag a négyszögletes háromszögek példáján. Ezután speciális formulákat nyitottak meg, amelyek lehetővé tették a használat határainak kiterjesztését a matematika ezen szakaszának mindennapi életében.

A trigonometria iskolai tanulmánya jelenleg négyszögletes háromszögekkel kezdődik, amelyek után a diákok a fizika tudását használják, és absztrakt trigonometriai egyenleteket oldanak meg, amelyekkel a felsőbb évfolyamokban kezdődik.

Gömb alakú trigonometria

Később, amikor a tudomány lépett a következő fejlettségi szint, az alábbi képlet szinusz, koszinusz, tangens, kotangens használták gömbi geometria, ahol különböző szabályok, és az összeget a háromszög szögei mindig nagyobb, mint 180 fok. Ez a rész nem tanítják az iskolában, de tudni a létezéséről kell lennie minimum, mert a Föld felszínét, és a felület bármely más bolygó, konvex, és így bármilyen felületen jegyekkel lesz három dimenziós térben „arc”.

Fogd a földgömböt és a szálat. Csatlakoztassa a szálat a világ bármely pontjára, hogy feszítse. Felhívjuk a figyelmet - megtalálta az ív alakját. Ilyen formákban alkalmazzák a gömb alakú geometriát, amelyet a geodézia, a csillagászat és más elméleti és alkalmazott területek használnak.

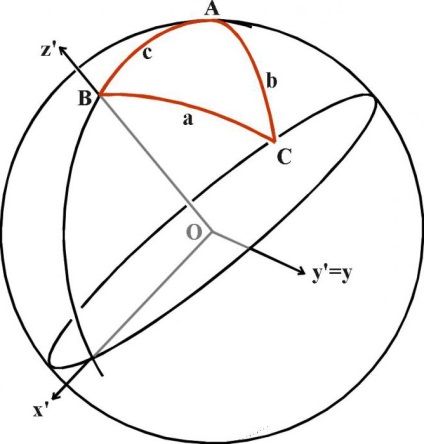
Négyszögletű háromszög

Kevés módszerek megismerése alkalmazása trigonometria, visszatérünk az alapvető trigonometria további megérteni, mi a szinusz, koszinusz, tangens, egyes számítások is használja őket, hogy végre, és milyen képletben használatra.

Mindenekelőtt meg kell érteni a jobb oldali háromszöghez kapcsolódó fogalmakat. Először is a hipoténusz az az oldal, amely a 90 fokos szöggel szemben helyezkedik el. Ez a leghosszabb. Emlékezzünk arra, hogy a pitagorai tétel szerint számszerű értéke megegyezik a másik két oldal négyzetének összegével.

Például, ha a két oldal 3 és 4 centiméter, akkor a hipotenus hossza 5 centiméter. Egyébként az ősi egyiptomiak körülbelül négy és fél ezer évvel ezelőtt tudtak erről.

A két másik oldalt, amelyek derékszöget képeznek, katettáknak nevezik. Emellett meg kell jegyeznünk, hogy a háromszög négyszögének összege egy négyszögletes koordinátarendszerben 180 fok.

meghatározás

Végül, a geometriai alap megértése végett megfordulhat a szinusz, a koszinusz és a szög meghatározása.

A szög sinusza az ellentétes láb (azaz a kívánt szöggel ellentétes oldal) aránya a hipotenusznak. A szög koszinusa a szomszédos láb és a hypotenuse aránya.

Ne feledje, hogy sem a szinusz, sem a koszinusz nem lehet nagyobb, mint egy! Miért? Mivel a hypotenuse alapértelmezés szerint a jobb háromszög leghosszabb oldala. Nem számít, mennyi ideig tart a katéter, rövidebb lesz a hypotenuse, ami azt jelenti, hogy arányuk mindig kevesebb mint egy. Így ha a probléma megoldásában egy szinusz vagy egy koszinusz értéke nagyobb, mint 1, keressen egy hibát a számításokban vagy az érvelésekben. Ez a válasz egyértelműen helytelen.

Végül a szög érintője az ellenkező oldal aránya a szomszédos oldalnak. Ugyanez az eredmény azt eredményezi, hogy a szinuszt a koszinusra osztják. Nézd: a képlet szerint osztjuk az oldalhosszúságot a hypotenuse segítségével, majd osztjuk a második oldal hossza és a hypotenuse szorozzuk. Így ugyanazt a kapcsolatot kapjuk, mint az érintő definíciójában.

A cotangent a sarok melletti oldal másik oldalához viszonyított aránya. Ugyanezt az eredményt kapjuk úgy, hogy az egységet az érintővel osztjuk el.

Tehát meghatároztuk a szinusz, a koszinusz, a tangens és a cotangent definícióját, és a képletekkel foglalkozhatunk.

A legegyszerűbb képletek

A trigonometria során nem lehet képletek nélkül - hogyan lehet szinusz, koszinusz, érintő, cotangent megtalálni nélkülük? De ez a probléma megoldásához szükséges.

Az első képlet, amelyet meg kell tudnia, amikor elkezdi a trigonometriát tanulni, hogy a szin és a koszin négyszögeinek összege egy. Ez a képlet a Pythagoras tételének közvetlen következménye, de időt takarít meg, ha tudni akarja a szög nagyságát, nem az oldalt.

Sok diák nem emlékszik a második képletre, amely szintén nagyon népszerű az iskolai problémák megoldásában: az egység összege és a szög érintkezési szögének négyszöge megegyezik a szög koszinusának négyzetével osztva. Vessünk közelebbről: ez ugyanaz a kijelentés, mint az első képletben, az identitás mindkét oldalát a cosin négyzetére osztották. Kiderül, hogy egy egyszerű matematikai művelet a trigonometriai képletet teljesen felismerhetetlenné teszi. Ne feledje: tudva, mi a szinusz, a koszinusz, a tangens és a cotangens, az átalakulási szabályok és számos alap formula, akkor bármikor le lehet következtetni a szükséges bonyolultabb képleteket egy papírlapra.

Kétszögű képletek és érvek hozzáadása

Két további képlet, amelyet szeretne megtanulni, a szinusz és koszinusz értékeihez kapcsolódik a szögek összegéhez és különbözeteihez képest. Az alábbi ábrán láthatók. Megjegyezzük, hogy az első esetben a szinusz és a koszin mindkét időpontban megszorozódnak, és a második esetben a szinusz és a koszinusz páronkénti termékét adják hozzá.

Vannak olyan képletek is, amelyek kétszög alakú érvekkel kapcsolatosak. Teljesen az előzőekből származnak - edzésként próbálják meg magukhoz vinni, ha a béta sarokkal megegyező alfa-szöget választanak.

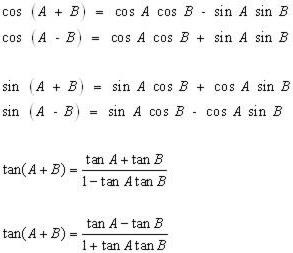
Végül vegye figyelembe, hogy a kettős szögű képletek átalakíthatók úgy, hogy csökkentsék a szinusz, koszinusz, tangens alfa fokát.

Az alap trigonometria két alapvető tétele a szinusz tétel és a koszinus tétel. Ezeknek a tételeknek köszönhetően könnyedén megértheted, hogyan találhatod meg a szinuszot, a koszinuszt és a tangent, és így az alak területét, az egyes oldalak méretét és így tovább.

A szinusz tétel szerint a háromszög mindegyik oldalának hosszát az ellenkező szög mennyiségével osztjuk meg, ugyanazt a számot kapjuk. Ráadásul ez a szám megegyezik a körülírt kör két sugarával, vagyis egy körrel, amely az adott háromszög minden pontját tartalmazza.

A koszinus tétel általánosítja a pitagorai tételt, amely háromszögekre mutat rá. Kiderül, hogy a két fél négyzetének összegéből a szomszédos szög kettős koszinusával megszorozzuk termékeiket - az így kapott érték megegyezik a harmadik oldal négyzetével. Így a pitagorai tétel a koszinus tétel speciális esete.

Figyelmeztető hibák

Még azt is tudva, hogy mi a szinusz, a koszinusz és a tangens, könnyű hibát okozni a figyelem vagy a hiba figyelmen kívül hagyása miatt a legegyszerűbb számításokban. Az ilyen hibák elkerülése érdekében megismerkedünk a legnépszerűbbekkel.

Továbbá vegye figyelembe, hogy minden háromszög esetében alkalmazható a koszinus tétel, de nem a Pitagorasz tétel! Ha tévedésből elfelejtened elvonni az oldalak duplázott termékét, szorozva a szög koszinuszával, akkor nemcsak teljesen rossz eredményt kapsz, hanem a téma teljes félreértését is. Ez rosszabb, mint egy figyelmen kívül hagyott hiba.

Harmadszor, ne keverd össze az értékeket a szögek 30 és 60 fok a szinuszok, koszinuszok, érintők, cotangents. Ne feledje ezeket az értékeket, mert a szinusz 30 fokkal egyenlő a koszinusz 60-mal, és fordítva. Ezeket könnyű összezavarni, ezért elkerülhetetlenül hibát fogsz kapni.

kérelem

Sok diák nem siet a trigonometria tanulmányozásához, mert nem értik az alkalmazott jelentést. Mi a szinusz, koszinusz, tangens egy mérnök vagy egy csillagász számára? Ezek a fogalmak, amellyel kiszámíthatod a távoli csillagok távolságát, megjósolhatod egy meteorit bukását, elküldhetsz egy másik bolygóra. Nélkülük nem tud építeni egy épületet, megtervezni egy autót, kiszámítani a terhelést a felszínen vagy az objektum mozgásának pályáját. És ezek csak a legnyilvánvalóbb példák! Végül is, az egyik vagy másik formában alkalmazott trigonometria mindenütt, a zenétől az orvostudományig terjed.

Végezetül

Szóval tudod, milyen szinusz, koszinusz, érintő. Számítások során felhasználhatja őket, és sikeresen megoldhatja az iskolai problémákat.

A trigonometria egész pontja lecsökken arra a tényre, hogy a háromszög ismeretlen paraméterei kiszámítják az ismeretleneket. Összesen ezek a paraméterek hat: a három oldal hossza és a három szög nagysága. Minden különbség a feladatok között van, hogy különböző inputokat adnak meg.

A szinusz, a koszinusz, a lábak ismert hossza vagy a hypotenuse megtalálása most már tudod. Mivel ezek a kifejezések csak kapcsolatot jelentenek, és az arány frakció, a trigonometrikus probléma fő célja megtalálni a szokásos egyenlet gyökereit vagy az egyenletek rendszereit. És itt a közönséges matematika segít.

Kapcsolódó cikkek

• Hogyan találjuk meg az érintőt a koszinuszon keresztül