Kirchhoff második törvénye
Kirchhoff második törvénye
- A stressz algebrai összege a komplex elágazó láncban tetszőlegesen kiválasztott zárt kontúr egyes szakaszaira esik, egyenlő az emf algebrai összegével ebben a kontúrban.
- A feszültség algebrai összege zárt hurokban esik, ami megegyezik az ebben az áramkörben levő emfs összegével. Ha az áramkörben nincs elektromotoros erőforrás, a teljes feszültségcsökkenés nulla.
- A feszültség algebrai összege az elektromos áramkör bármely zárt áramköre mentén nulla.
- A passzív elemek feszültségének algebrai összege megegyezik az EMF algebrai összegével és az áramkörben működő áramforrások feszültségével.
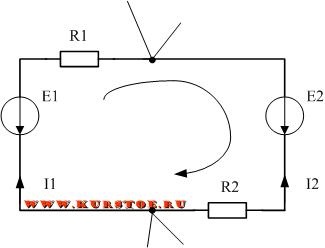
Ie az R1 jelén keresztüli feszültségcsökkenés és az R2 jelzéssel ellátott feszültségcsökkenése megegyezik az emf 1 forrásának feszültségével, annak jelével, valamint a jelzőjellel ellátott feszültséggel a 2 elektromotoros erő forrásával. Az algoritmust a tábláknak a Kirchhoff-törvény szerinti egyenletekbe történő rendezésére egy külön oldalon ismertetjük.
Kirchhoff második törvényének egyenlete
A második Kirchhoff-törvény szerint különböző módon hozhat létre egyenleteket. A legalkalmasabb az első képlet.
Ezen egyenletben egyenleteket is írhat.
Kirchhoff második törvényének fizikai jelentése
A második törvény egy kapcsolatot állapít meg az elektromos áramkör zárt részének feszültségcsökkenése és az EMF források ugyanazon zárt területen történő működésével. Ez összefügg az elektromos töltés átadásával kapcsolatos munka koncepciójával. Ha a díjátadást zárt hurkon hajtja végre, visszatér ugyanarra a pontra, akkor a tökéletes munka nulla. Ellenkező esetben az energia megőrzésének törvénye nem teljesülne. A potenciális elektromos mező e fontos tulajdonsága Kirchhoff 2. szakasza az elektromos áramkörnek.