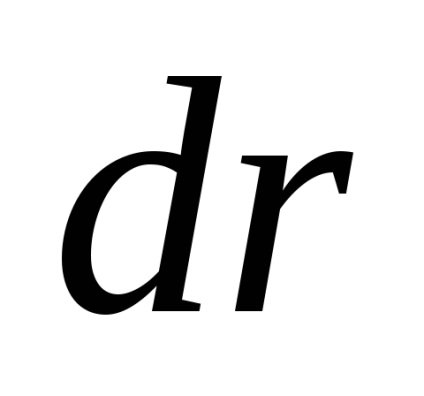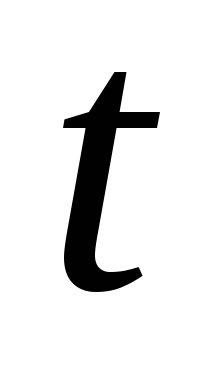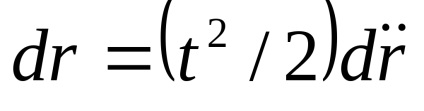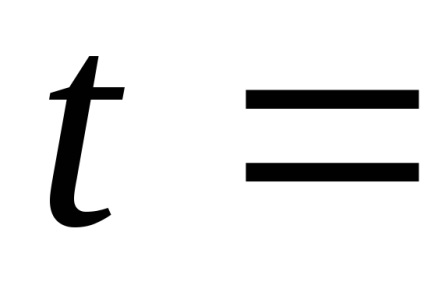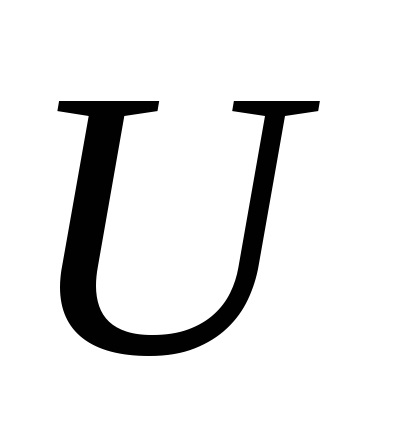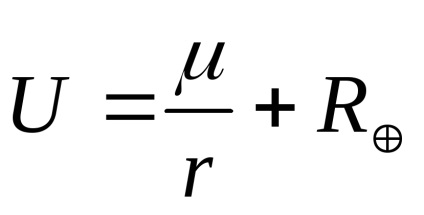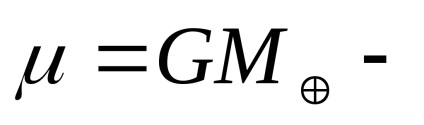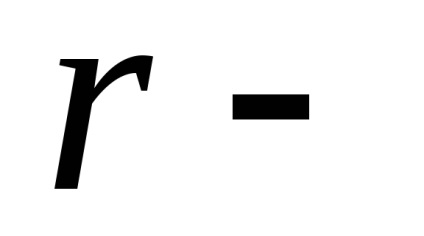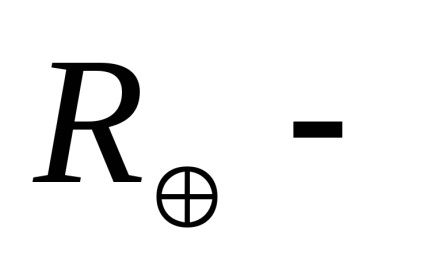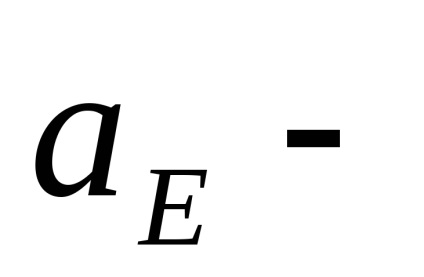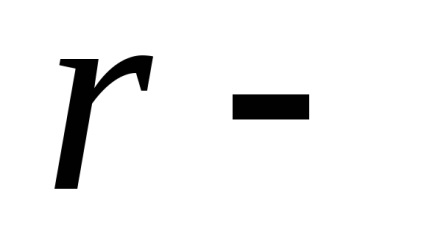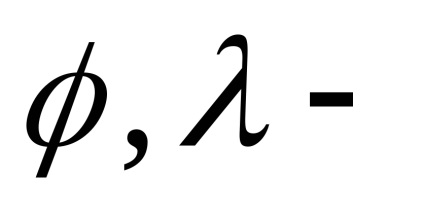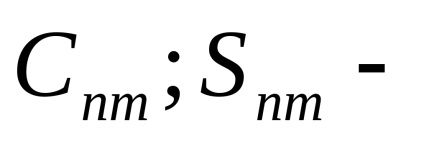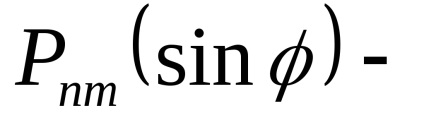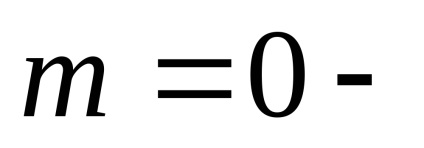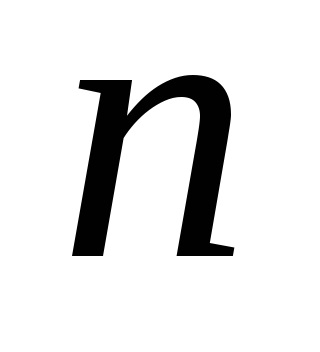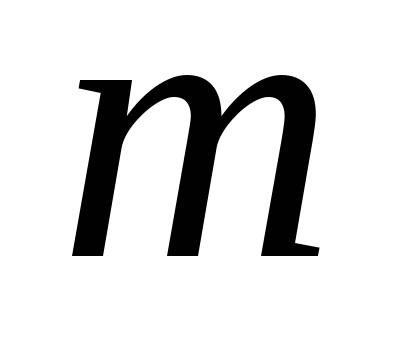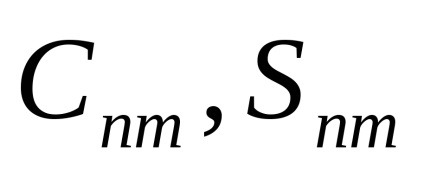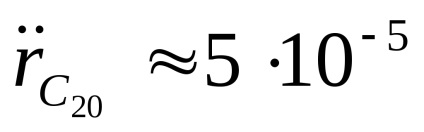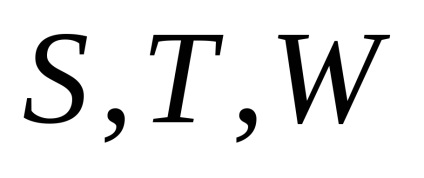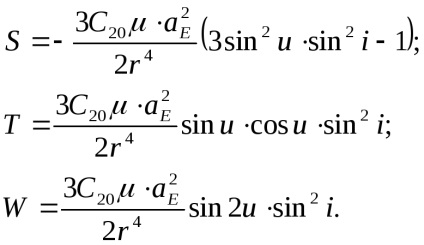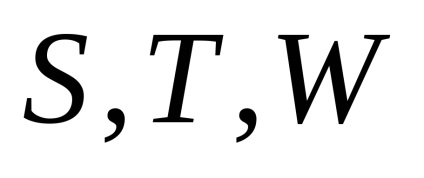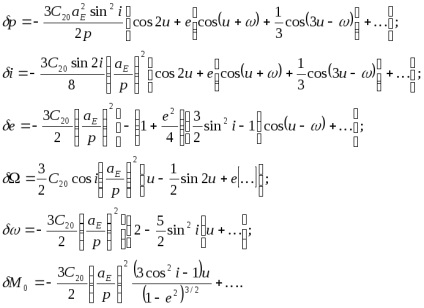A gravitációs és nem gravitációs jellegű perturbációk többféle formája a rádiónavigációs rendszerek műholdaként működik. Annak a ténynek köszönhetően, hogy a műholdak körülbelül 20 000 km magasságban forognak, a tükrözött napsugárzás és a légellenállás hatása elhanyagolható. Például a szabálytalan alak, és következésképpen a műholdak keresztmetszeteinek különbségei megnehezítik a közvetlen napsugárzás nyomásának modellezését. A műholdak gyártására használt különféle anyagoknak különböző a hőelnyelés jellemzője, ami további nehézségeket okoz a gyorsuló gyorsulás figyelembevételével.
A perturbáló gyorsulások hatása a következő példa alapján megítélhető: hagyja, hogy a műholdas rendszer folyamatosan gyorsuljon
a lehetőség. = 10 -9 m / s 2. Kapcsolódó elmozdulás vele
a műhold helyzetében az idővel történő kettős integráció után
kapott mint
a lehetőség. . A mennyiség helyettesítése
12 óra, az SRNS műhold eltolását egy forradalom után kapjuk meg, ami egyenlő
≈ 1 m. Ez az eltolódások tipikus értékének tekinthető.
A Föld gravitációs potenciálja.
A Föld gravitációs potenciálja
Külső ponton lehetséges megjeleníteni a következő formában:
,
ahol
geocentrikus gravitációs állandó;
geocentrikus távolság a külső pontnál;
zavaró része a geopotenciális. A jobb oldali első kifejezés meghatározza a zavartalan mozgást (egy labda vagy egy pont potenciálja), a második kifejezés meghatározza a műholdas mozgás perturbációját.
A perturbációs potenciál általában egy gömb alakú funkciók terjeszkedésének formájában adódik:
,
ahol
a Fél semimajor tengelye;
a műhold geocentrikus távolsága;
annak szélességi és hosszúsági fokát. Az értékek
dimenzió nélküli koefficiensek, amelyek a Föld külső gravitációs mezőjét jellemzik. végül
Legendre funkciók (gömb funkciók), amelyek kétféleképpen oszlanak meg:
Legendre polinomokat és a Legendre kapcsolódó funkcióit. egészek
és
a bővítés mértéke és sorrendje.
A Legendre polinomokat a Rodrigue-képlet alapján határozzuk meg:
,
számukra a visszatérő kapcsolat
.
Az első két polinom kifejezésének formája:
A mellékelt Legendre funkciók kifejezései:
A gömb alakú függvények zónai, ágazati és szöveti (mozaikos) részekből állnak, a gömb vonalától függően, melyekkel a különböző harmonikus jelek régiói vannak rajzolva.
Pozitív és negatív értékek:
a) a zónában; b) szektoriális; c) a potenciál szövetszerkezeteire.
A harmonikus bomlás koefficiensei
különböző potenciális modellekről ismertek. A műholdak mozgására a legnagyobb hatás a Föld egyenlítői tömörítéséhez kapcsolódik a második zóna harmonikus együtthatójával. A kompresszió következtében fellépő perturbáló gyorsulás maximális értéke
cm ∙ s -2. A potenciális harmonikusok fennmaradó együtthatója ezerszer kisebb, és ennek megfelelően az általuk kifejtett hatás kisebb.
A Föld tömörítésének zavaró szerepe:
Zavaró gyorsulások
kifejezést a következő kifejezések képviselik:
A helyettesítés után
A differenciálegyenlet a simuló pályaelemek és integráció az 1. közelítés, azzal a feltétellel, hogy r = 1, és az összes elem állandó, kivéve megfontolás alatt, három elem kap kapcsolatos zavarok idő paraméterét szélességi vagy
:
A három utolsó képletben a perturbációk lineárisan kapcsolódnak a szélességi érveléssel
. Az ilyen perturbációkat szekulárisnak nevezzük, és a perturbációs elméletben e három elemet (hosszúság, perigéz argumentum és átlagos anomália) szögelemnek nevezzük. Perturbációk okozta összenyomott föld vezet az orbitális keringési síkja forgástengelye körül (precesszió pályára), és forog a pályasíkon. A pozícióelemekben, amelyek magukban foglalják a dőlést, az excentricitást és a fókuszparamétert, csak rövid ideig kompressziós perturbációk vannak.
A műholdas rádiónavigációs rendszerek korai éveiben a 8. sorrendig és a fokozathoz viszonyított együtthatókat elegendőnek ítélték több íves műholdak számára. Ezzel kapcsolatban az ellenőrzés referenciakeret meghatározása során pontosan kering a Föld gravitációs modell segítségével együttható készletek a megrendelések száma és a hatalom a komponens több tíz vagy akár több száz.
Kapcsolódó cikkek