inflexiós pont

A grafikon az inflexiós pont

Definíció. A grafikon pont az úgynevezett inflexiós pont ez a grafikon, ha létezik egy olyan környéken, a vízszintes tengelyen, amelyen belül a grafikont a jobb és bal oldalon a ponton különböző irányokba convexity.

Ha a függvény differenciálható a ponton és környékén, a geometriailag ez azt jelenti, hogy a grafikon az áthaladások közelében egyik oldalán az érintési pont egy másik (3.).

Ha a függvény folytonos címen. differenciálható a környéken. kivéve a lényeg. és. A grafikon a funkciót a pont szomszédságában található ellentétes oldalán a függőleges érintő (ábra. 4).

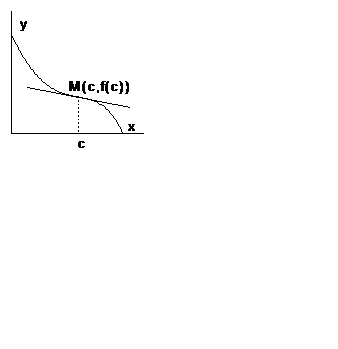
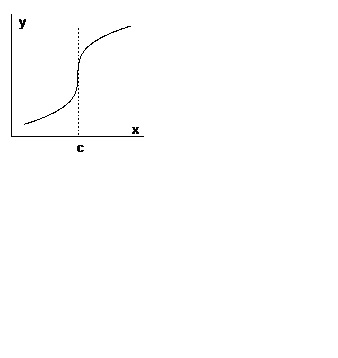
3. Tétel (szükséges feltétel megléte az inflexiós pont). Tegyük fel, hogy a függvény folytonos a ponton a második derivált. Ezután, ha a pont egy inflexiós pontot a grafikon, akkor.

Megjegyezzük, hogy a feltétel szükséges, de nem elégséges feltétele az inflexiós A grafikon a pont. Vegyük például azt a funkciót. A második deriváltja ezt a funkciót. nullpont. Azonban az egész valós tengelyen. ezért mindenütt a grafikonja ez a tengely konvex lefelé, és a pont nem egy inflexiós pont.

Tétel 4 (elégséges feltétele az inflexiós pont). Ha a függvény differenciálható a ponton. kétszer differenciálható egy pont szomszédságában. kivéve talán a legtöbb pontot, és a második derivált előjelet, amikor áthalad a ponton az érvelés. a lényeg az inflexiós pont a függvény grafikonját.

Megjegyzendő, hogy ha a függvény folytonos. kétszer differenciálható egy pont szomszédságában. kivéve a lényeg. és egy érintője azon a ponton (legalább a tengellyel párhuzamosan), majd az az állítás, a 4. tétel is igaz.

1. példa Keresse az inflexiós pont a függvény grafikonját.

Találunk-származékok meghatározott függvény:

nullává válik a pontokat. és előjelet, ha átmegy ezeken a pontokon. Ezért a pontokat és inflexiós pontjait a grafikon funkciók. Megjegyezzük továbbá, hogy a szünetekben és. így, a grafikon a függvény konvex, felfelé irányuló. At intervallumban. és ütemezés funkció van egy convexity lefelé irányul.

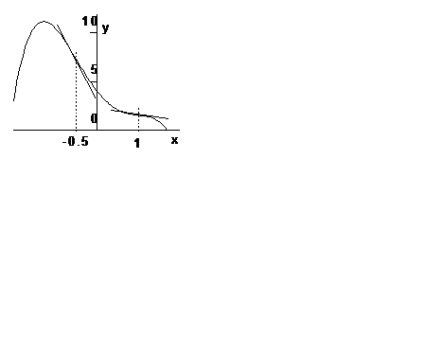
Példa 2. Keresse meg az inflexiós pontot a grafikon funkciók.

Ez a funkció folytonos az egész valós tengelye körül, és

végleges második derivált mindenhol a számot sorban, kivéve a pont. És mikor. és mikor. Annál a pontnál az első függvény deriváltját nincs definiálva. Mert. A grafikon a függvény az a pont (1,2) függőleges tangensét. Mivel a második derivált előjelet, amikor áthalad a ponton. A pont (1,2) van egy inflexiós pontot.

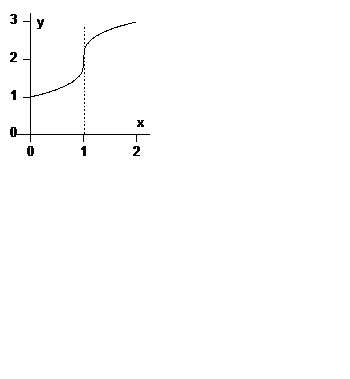
Az irány a grafikont a konvexitás

Hagyja, hogy a függvény differenciálható bármely időpontban. azaz, azt bármely pontján az intervallum véges származékot. Aztán ott van az érintő a függvény grafikonját. áthaladó bármely pontján a grafikonon. ahol az érintő nem párhuzamos a tengellyel.

Definíció. Azt mondják, hogy a grafikon az intervallum konvex lefelé (felfelé), ha a grafikonja ez a funkció nem kevesebb, mint (nem nagyobb, mint) bármely érintője.

Ábra. Az 1. ábra egy grafikon, amely konvex lefelé, ábrán látható. 2 - konvex, felfelé irányuló.

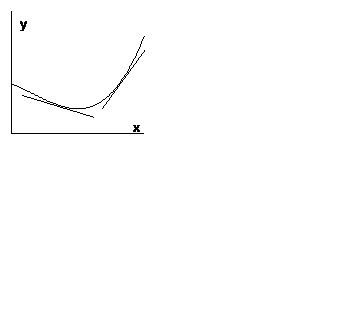
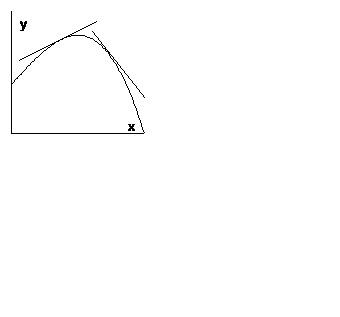
1. Tétel Ha a funkció az intervallum akkor ér véget, a második derivált és ezt a származékot nem negatív (nem pozitív) az egész ezen a tartományon, a függvény grafikonját az az időköz konvexitás lefelé irányul (felfelé).

2. Tétel Tegyük fel, hogy a második derivált folyamatos és pozitív (negatív) azon a ponton. akkor létezik egy pont szomszédságában. amelyen belül a függvény grafikon konvex lefelé (felfelé).

Kapcsolódó cikkek

előző ◈ a következő