A tulajdonságait a számtani átlaga
A számtani átlaga számos matematikai tulajdonságokkal, hogy lehet használni, hogy egyszerűsítse a számításokat. A fő tulajdonságait egy ilyen számtani átlag.
1. A számtani átlaga konstans értékét konstans:
2. A négyzetösszege eltérések számtani átlaga mindig kevesebb, mint a négyzetes eltérések más értékek:
3. Az érték az átlagos nem fog változni, ha a gyakorisági eloszlását számos helyettesítő relatív gyakorisága.
4. Az összeg az egyes jellemző értékei eltérések az átlagos, megszorozzuk tömeg (frekvencia) nulla:
£ (x - x) = x - nx = 0 - az egyszerű átlagos;
5. Ha az összes jellemző értékek nő vagy csökken az azonos tényező (k), az átlagos (x) nő vagy csökken ugyanazzal a tényezővel:
vagyis az átlagos csökkenés (a) újra.
6. Ha az összes beállítást értékek (x) elvenni, adjunk nekik ugyanaz a konstans érték (x0), az átlagos (x) csökkentéséhez vagy növeléséhez, az azonos mennyiségű (ho)
azaz, az átlagos csökkent állandó számú x0.
7. Ha a frekvencia (tömege) osztva, vagy szorozva bármilyen konstans számú (k), akkor az átlag nem változik:
azaz az átlagos érték nem változott.
8. A termék átlagos összegére frekvencia összege munkálatok a frekvencia változat:
Ez az egyenlet következik tulajdonságait meghatározó számtani átlaga, amely szerint, összehasonlítva a kiviteli alakoknál, biztosítva számukra ugyanazokat az értékeket helyettesítve átlagos értéke, teljes térfogata változatlan marad funkciót.
9. A teljes átlagos átlaga a privát szekunder súlyozott száma vonatkozó részeit (csoportok) együtt:
A fentiekben ismertetett tulajdonságok egyszerűsíti a számtani átlaga a számítás: az összes lehetséges jellemző értékeket levontuk tetszőleges konstans értéket kapott különbség osztva az intervallumot, majd szorozva a kiszámított átlagérték intervallum, és adjunk hozzá egy tetszőleges állandó értékre, amely figyelembe, mint a származási.
A képlet a számtani átlaga egy egyszerűsített módszer a következő:
ahol x = --umenshena számtani átlaga;
x = a ° - alakváltozás időközönként; x0 - az eredete;
k - érték intervallum.
Az átlagos értéke x - az úgynevezett első momentum, és kiszámításának módszerét átlagos módszer vagy eljárás hivatkozási pont a névleges kezdet.
Feltételes eredetű (x0) rendszerint az egyik érték varіyuchoї jeleket, amelyeket általában központjában néhány forgalmazás vagy az egyik, hogy a legmagasabb frekvencia.
Tekintsük a példát meghatározása az átlagos szám intervallum aritmetikai elosztási eljárás pontot, eloszlási adatokat 100 gazdaságok tejhozamot tehénre (lapon. 4.7).
Feltételes eredetű (x0) vegye az egyik érték az intervallum közepén található egyes forgalmazási és ahol a legmagasabb frekvencia. A mi a probléma ez az érték x0 = 33 p. A nagysága az intervallum k = 2 n.
A táblázat szerint határozzák meg a hagyományos (kisebb) a számtani átlaga:
4.7 táblázat. Az adatok kiszámításához számtani közép intervallumban számos módon történő szétosztása pontok
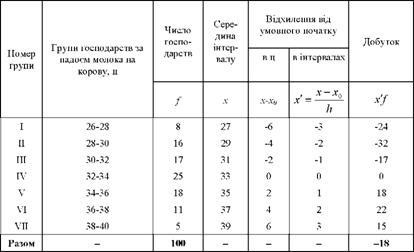
Ahhoz, hogy a tényleges átlagos termelés a tehenek módosítani kell:
Így kapjuk ugyanazt az eredményt, mint a táblázat adatai. 4.2. Az eredményeket a számtani átlaga két módon egybeesett.