A koncepció a mérési bizonytalanság
A gyakorlati alkalmazás során a különböző mérési fontos felmérni azok pontosságát. A „pontosság”, azaz a. E. mértékben közelíti a mérési eredmények néhány valódi érték nem szigorú meghatározások és mérésére alkalmazott minőségi összehasonlítást műveleteket. Számszerűsíteni kell alkalmazni a „mérési hiba” (minél kisebb a hiba, annál pontosabb).
Híváshiba eltérése a mérési eredmény a tényleges (valós) A mért nagyságát HN. Meg kell jegyezni, hogy az igazi érték egy fizikai mennyiség tekinthető névtelen és használják az elméleti munkákban. A tényleges érték egy fizikai mennyiség által meghatározott kísérlet a feltételezés, hogy a kísérlet eredményét (mérés) a legnagyobb mértékben, közel a valódi érték. Egy hiba a mérési - az egyik legfontosabb intézkedések nyomon követhetőség biztosítására.
Mérési hibák általában a műszaki dokumentáció mérőeszközök vagy rendeletek. Azonban ha figyelembe vesszük, hogy a hiba is függ milyen feltételek mellett végzett mérési maga a kísérleti hiba módszereket és szubjektív jellemzői a személy abban az esetben, ha azt közvetlenül részt vesznek a mérések beszélhetünk több összetevője mérési hiba, vagy az összes hiba .
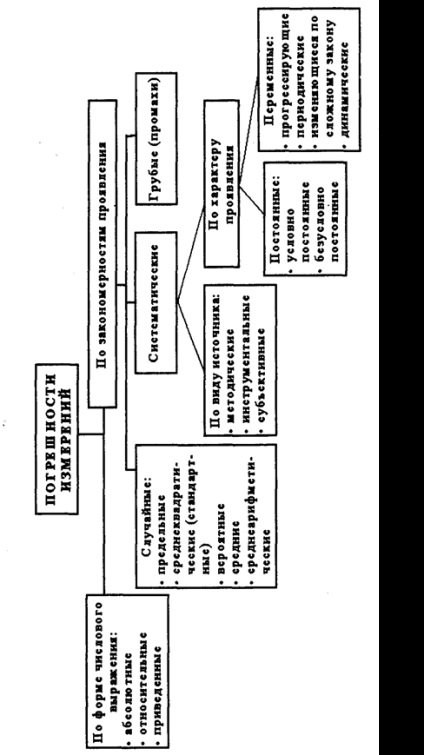
A számos tényező befolyásolja a mérési pontosságot elég nagy, minden osztályozási és mérési hibák (2. ábra), hogy egy bizonyos mértékig önkényes, mivel a különböző hiba függően a mérési körülményektől a folyamat jelennek meg a különböző csoportokban.
2.2 hibatípusok
A mérési hiba - ez az eltérés a mérési eredmény X a valódi mért érték Hi. Annak megállapítására, a mérési hibák helyett a valós fizikai érték Hi. ténylegesen használni a tényleges érték XA.
Attól függően, hogy a kifejezés formája megkülönböztetni az abszolút, relatív és csökkentett mérési bizonytalanságot.
Az abszolút hiba különbségként határoztuk meg # 916; = X - vagy Hee # 916; = X - Xg. és a relatív -, mint az arány # 948; = ± # 916; / CD # 903; 100%.
csökkentett hiba # 947; = ± # 916; / # 935; # 925; 903 #; 100%, ahol # 935; N - normalizálás mennyiség értéke van, mint a mérési tartomány az eszköz, a felső határ a mérési, stb
A számtani középértéke szolgál a valódi értékét több mérést a paraméter:
ahol Xi - i -edik mérési eredmény, - n a mérések száma.
Mennyiség. így a mérések egy véletlen megközelítést Hee. Annak megállapítására, hogy a lehetséges eltéréseket Hee meghatározó becsült szórása számtani közepe:
Ahhoz, hogy értékelje a szórási Xi egyes mérési eredmények tekintetében a számtani átlagát a minta átlagos meghatározzuk eltérés:
Ezek a képletek mellett használják a feltétellel, állandó intézkedés értéke a mérés alatt.
Ezek a készítmények megfelelnek a centrális határeloszlástétel valószínűségszámítás, hogy a számtani átlaga egy méréssorozat mindig kisebb hiba, mint a mérési hiba az egyes adott:
Ez a képlet tükrözi alaptörvénye elmélet hibák. Ebből az következik, hogy ha szükség van, hogy növelje a pontosságát az eredményt (ha a kizárt rendszeres hiba) 2-szer, majd a mérések száma növelni kell 4-szeres; Ha azt szeretnénk, hogy növelje a pontosság 3-szor, a mérések száma
nőtt 9-szer, stb
Meg kell világosan megkülönböztetni a mennyiség alkalmazása és az S # 963;: első értékelés során használt, a végső kimenetelét a hiba, és a második - a mérési bizonytalanság kiértékelése a módszer. A legvalószínűbb hiba egy mérés # 916; a 0,67 S.
Jellegétől függően a tünetek, okok és megoldások orvosolni megkülönböztetni szisztematikus és random mérési hiba, és hibákat (baklövések).
A rendszeres hiba állandó marad, vagy változik rendszeresen ismétlődő mérések ugyanazon paramétert.
Véletlen hiba változik az azonos mérési körülmények véletlenszerűen.
Hibákat (hibák) fordulhat elő, mert a hibás intézkedések az üzemeltető, a kudarc mérőeszközök vagy hirtelen változások mérési körülmények között. Általános szabály, hogy a jelentős hibákat észlelt feldolgozásával a mérések eredményeit a konkrét feltételeket.
Véletlenszerű és szisztematikus hiba összetevői mérések kimutatták, egyszerre, úgy, hogy az összes hiba, az összege a hibákat függetlenségüket.
Az érték a véletlen hiba nem ismert előre, ez miatt előfordul, hogy több nem specifikált tényezők. Kizárás az eredményeket a véletlenszerű hibák nem, de hatásuk lehet csökkenteni feldolgozása a mérési eredményeket.
Gyakorlati okokból fontos tudni, hogyan kell megfogalmazni a követelményeket a pontosság. Például, ha a megengedett gyártási hiba, hogy # 916; 3 = # 963;, majd, növelve a pontossági követelmények (például legfeljebb # 916; = # 963;), miközben a gyártási technikák növeli a valószínűségét a házasság.
Általában úgy tartják, hogy a szisztematikus hibák mo-gut kell kimutatni és megszüntetni. Azonban a valóságban teljesen megszünteti ezek a hibák lehetetlen. Mindig marad valami Unexcluded maradványok kell figyelembe venni, hogy értékelje a határokat. Ez lesz a szisztematikus mérési hiba.
Más szóval, az elv a rendszeres hiba, túl véletlenszerű és ez a felosztás csak köszönhető, hogy a kialakult hagyományok a feldolgozása és bemutatása a mérési eredményeket.
Ellentétben véletlen hiba, amely egészében, függetlenül annak forrásától, a rendszeres hiba látható komponensek függően forrásait annak előfordulása. Különbséget szubjektív, módszertani és műszeres összetevői hiba.
A szubjektív eleme a hiba, amely az egyéni jellemzőit az üzemeltető. Jellemzően ez a bűnös-ség miatt előfordul, hogy a hibákat a kiolvasás (0,1 osztás) és a helytelen üzemeltető képességeit. Alapvetően rendszeres hiba fakad Módszertani és szerszám alkatrészek.
Cikkek hibakomponens miatt tökéletlenség mérési módszer, módszerek segítségével mérési eszközökkel, helytelen számítási képletek és kerekítési eredményeket.
Műszeres komponens keletkezik, mert a saját hiba mérőeszköz meghatározza a pontossági osztály, befolyása a mérőműszerek az eredményt a korlátozott felbontás és vérnyomásmérés.
A célszerűségét szétválasztása rendszeres hiba, a módszeres és műszeres komponensek magyarázata a következő:
- hogy javítsa a mérés pontosságát tudja különböztetni a korlátozó tényezőket, és így dönt a javulás a technika vagy szelekciós pontosabb mérési eszköz;
- lehetővé válik, hogy meghatározzák a teljes hibakomponens hogy növekszik az idővel, vagy befolyása alatt a külső tényezők, így céltudatosan végezze a rendszeres ellenőrzés és tanúsítás;
- eszköz komponens lehet értékelni módszerek kifejlesztése és a potenciális pontosságát képességeit a kiválasztott módszer meghatározása csak módszertani komponens.
2.3 mérő mutatók minőségét
Unity mérések azonban nem lehet elérni csak véletlen hibák. Amikor mérések is fontos tudni, hogy a minőség a mérési paramétereket. Által minőségének mérésére értik meg a tulajdonságokat, amelyek meghatározzák az eredmények a készítmény a kívánt pontosságot jellemzőit, a kívánt módon és időben.
mérések minőségének jellemzi mutatók, mint a precizitás, pontosság és megbízhatóság. Ezek a mutatók alapján kell meghatározni úgy becsüli, hogy meg kell felelnie a következetesség és a hatékonyság torzítatlanság.
Az igazi mért érték eltér a számtani középértéke az eredmények a megfigyelések szerint az összeg a rendszeres hiba # 916; s. .., vagyis X = - # 916; s. Ha a rendszeres komponens ki van zárva, akkor X =.
Azonban, mivel a korlátozott megfigyelések száma, és az értéke nem lehet pontosan meghatározni. Akkor csak becsülni az értékét, meg egy bizonyos határértéket, a tartomány, amelyben található. Értékelés számjegyadatot X forgalmazási szabályokat, pedig egy pont a valós tengelyen nevű ragya. Ellentétben számszerű jellemzők értékelés valószínűségi változók, és értékük függ n számát. Egyenletes hívás értékelést, hogy ha n → ∞ a valószínűsége csökkent a becsült érték.
Úgynevezett tárgyilagos értékelést, a várakozás megegyezik a becsült érték.
Tényleges lehívása ezt az értékelést, amely a legalacsonyabb diszperziós # 963; 2 = min.
Listás követelmények megfelel a számtani középértéke az eredmények n megfigyelések.
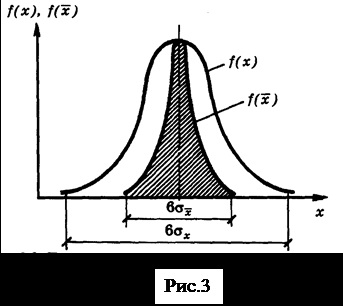
Tehát egyetlen mérési eredmény egy valószínűségi változó. Ekkor a mérés pontosságát - a szomszédságában a mérési eredményeket a valódi értékét a mért érték. Ha a rendszeres hiba alkatrészek vannak zárva, a mérési eredmény pontossága jellemzi mértéke a szórás értéke, azaz. E. diszperziós. Amint azt fent említettük, a diszperzió a számtani közép # 963; n-szer kisebb, mint a diszperziós egyedi eredmények a megfigyelés.
A mérések megbízhatóságát az eredmény bizalmának mértéke határozza meg, és annak a valószínűsége, hogy a mért mennyiség valós értéke a tényleges érték jelzett környezetében van. Ezeket a valószínűségeket bizalmasnak hívják, és a határok (szomszédságok) megbízható határok. Más szóval, a mérés megbízhatósága a nem kizárt szisztematikus hiba nullához közeli.
Bizalmi intervallum határértékekkel (vagy bizalmi limitekkel) # 916; d-tól + -ig # 916; q a véletlen hiba értéktartománya, amely adott Pd konfidencia valószínűséggel. a mért mennyiség valós értékét tartalmazza.
pg<- Δд ≤,Х ≤ + Δд>.
Egy kis mérések számának (n 20), és a használata a rendes törvény nem lehet meghatározni a konfidencia intervallum a normális eloszlás írja le a viselkedését a véletlen hiba elvileg végtelen számú dimenziók.
Ezért alkalmazzák, vagy Student eloszlás kis számú mérést - eloszlás (javasolt angol statisztikus Gosset közzé néven „hallgató”), amely lehetővé teszi a meghatározását megbízhatósági intervallumok egy korlátozott számú mérés. A konfidenciaintervallum határait a következő képlet határozza meg:
ahol t a Student eloszlás együtthatója, az adott Pd konfidencia valószínűségtől és a n.
A növekvő számú megfigyeléssel a Diák eloszlása gyorsan megközelíti a normál értéket, és már n ≥30-nál is egybeesik.
Meg kell jegyezni, hogy a megbízhatóságot nem biztosító mérések eredményei, vagyis a megbízhatóságuk bizonyos fokú megbízhatósága, nem értékesek. Például egy mérőkör érzékelője nagyon magas metrológiai jellemzőkkel bírhat, de a telepítésből, a külső körülményekből, a rögzítési módokból és a jelek feldolgozásából eredő hibák nagyméretű véges mérési hibához vezetnek.
Az olyan mutatók mellett, mint a pontosság, megbízhatóság és pontosság, a mérési műveletek minőségét az eredmények konvergenciája és reprodukálhatósága jellemzi. Ezek a mutatók legáltalánosabbak a vizsgálatok minőségének értékelésénél és pontosságuk jellemzésénél.
Nyilvánvaló, hogy ugyanazon módszer két vizsgálata ugyanazt a módszert nem adja meg azonos eredményeket. Objektív mértéke statisztikailag érvényes becslésekként szolgálhat a két vagy több, a módszerük szigorú betartása mellett nyert vizsgálatok eredményének várható közelségével. A megfelelőség és a reprodukálhatóság mint a statisztikai értékelés a vizsgálati eredmények konzisztenciájáról.
A konvergencia két, egy módszerrel, ugyanazon berendezéssel, egy laboratóriumban elért eredmények közelítése. A reprodukálhatóság különbözik a konvergenciától, mivel mindkét eredményt különböző laboratóriumokban kell elvégezni.
3. A MÉRET EREDMÉNYEINEK NYÚJTÁSÁNAK ÉS REPREZENTÁCIÓJA
3.1 A mérési kísérlet leírása
Mérési kísérlet létrehozásakor mindenekelőtt meg kell határozni, hogy mely méréseket kell elvégezni (egy vagy több) a mért fizikai mennyiség értékének meghatározására. A következő megközelítés gyakori:
Ha a szisztematikus hiba a meghatározó hiba, pl. értéke sokkal nagyobb, mint a véletlen hiba értéke, akkor célszerű egy mérést alkalmazni a mért mennyiség értékének megszerzéséhez;
Ha a véletlen hiba a meghatározó hiba, akkor több mérést kell használni.
Figyelembe kell venni, hogy a szisztematikus hiba a mérési eredmények elmozdulását okozza, és a legveszélyesebb, ha nem feltétlenül létezik. A szisztematikus mérési hiba felismerése a metrológia egyik legnehezebb feladata. Az egyik vagy másik formában a mérések előkészítésekor mindig el kell dönteni.