A fenti négyszög
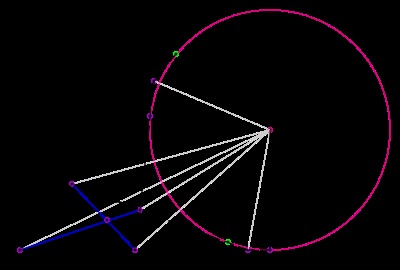
A fentiekben leírt ABCD négyszög és annak kifelé körülírt köre
A fenti négyszög egy konvex négyszög. amelyeknek mind a négy oldala folytonosan érintkezik a körrel (a négyszögön kívül) [1]. A kört vázlatnak nevezik. A körülírt kör középpontja hat határoló metszéspontja. Ez a felezővonal két szemközti belső szöge egy négyszög szögei felezővonal a külső szögek a másik két csúcsot, és a külső bisectors szögek a metszéspontja a kiterjesztését ellentétes oldalán (lásd a jobb oldali kép, a továbbiakban a folytatása a felek tartott szaggatott vonal). Ex-érintőnégyszög szoros kapcsolatban leírtakhoz négyszög (amelynek négy oldala pedig érinti a kör).
A deltoidok egy példa a négyszögekre, amelyeket nem írtak le. Paralelogrammák (amelyek magukban foglalják a négyzetek. Gyémántok és téglalapok) tekinthető ex-érintőnégyszög végtelen sugárral excircle ha eleget tesznek a tulajdonságok az alábbiakban leírt, de vneopisannaya kerülete nem érintheti az oldalán, a két pár kiterjesztés (miatt párhuzamosság) [2]. Konvex négyszögek, amelyek oldalhosszai aritmetikai progressziót alkotnak. mindig nem írják le, mivel megfelelnek az alább ismertetett feltételeknek a szomszédos oldalak számára.
A konvex négyszög nem írható le, ha és csak akkor, ha. amikor egy ponton hat egymást keresztező szelvény van. Ez felezővonal két belső sarkai a négyszög szemközti szögek felezővonal külső sarka és két másik csúcsa felezővonal külső sarkok a kereszteződési pontokon a meghosszabbításai szemközti oldalán [2].
A számítások szempontjából hasznosabb, ha az a, b, c, d oldalú domború négyszög a leíráson kívül van, ha és csak akkor, ha a két szomszédos oldal összege megegyezik a másik két oldal összegével. Ez két esetben lehetséges
Az ingatlanot Jacob Steiner 1846-ban igazolta [3]. Az első esetben excircle van a nagyobb szögek a csúcsokat A vagy C. mivel a második esetben a kör oldalán a nagyobb szögek a csúcsok a B és D Van másikra ABCD négyszög egy = AB hossza. b = BC. c = CD és d = DA. A kapott két egyenlőség kombinálásával megkapjuk, hogy az ellentétes oldalak különbségeinek abszolút értéke egyenlő [2],
Ez az egyenlet szorosan kapcsolódik a Pitot-tételhez a leírt négyszögek esetében. amelyen az ellenkező oldalak összege egyenlő.
Urquhart tétele
Ha az ABCD konvex négyszög ellentétes oldala metszi az E és F pontokat, akkor
A balról jobbra történő származást LM Urkhart (1902-1966) után nevezték el, bár Augustus de Morgan 1841-ben már régen bizonyította. Daniel Pedoe (Daniel Pedoe) ezt az állítást az euklideszi geometria legelemibb tételének nevezte. mivel csak a közvetlen és távolságokkal foglalkozik [4]. Az egyenértékűséget Mowaffac Hajja [4] igazolta. amely a jobb oldalon egy egyenlőséget teremtett egy másik szükséges és elegendő feltételnek ahhoz, hogy a négyszög a leíráson kívül legyen.
Összehasonlítás a leírt négyszöggel
A leírt négyszögek több mutatója (a táblázat bal oszlopa) nagyon hasonlít a megfejtett négyszögekhez (a táblázat középső és jobb oszlopai), amint az az alábbi táblázatban látható [2]. Így egy konvex négyszögnek van egy ívelt vagy körkörös körvonala a megfelelő csúcs körül (az oszloptól függően), ha és csak akkor, ha az öt feltétel közül bármelyik megtartja.
Bug-inok A vagy C előtt
Írva kívül B vagy D