Poliéder poliéder és tanulmány egy általános iskolában
Történelmi tájékoztatás a rendszeres poliéder ............... .. ... 0,9
Rendszeres polyhedra körülöttünk ..................................... 14
A téma a „Polyhedra” az egyik legfontosabb hagyományos iskolai geometria természetesen. Ők alkotják, mondhatni, a központi témája a szilárd geometria. A tanulmány a párhuzamos és merőleges vonalak és síkok a diéderes szögek és a többi, valamint a bevezetése vektorok és a koordináták - mindez csak a kezdete szilárd geometria, előkészítő eszközök a tanulmány annak érthetőbb tárgyak - főként szilárd anyagok és felületek.
A központi szerepet Poliéderek elsődlegesen meghatározza az a tény, hogy sok az eredmények, amelyek más szervek, amelyek szerint a megfelelő eredménye poliéder; Elég csak felidézni meghatározását nagyságát és alapterületét a szervek azáltal, hogy a határ poliéder.
Ezen túlmenően, a poliéderek maguk rendkívül értelmes vizsgálat tárgya, állt ki az összes szervei sok érdekes tulajdonságokkal, főleg a vele kapcsolatban álló tételek és problémák. Akkor például felidézni az Euler-tétel az arcok számát, élek és csúcsok, a szimmetria a rendszeres poliéder, a kérdés a térkitöltő poliéder, és mások.
Polyhedra kell adni egy iskolában természetesen nagyobb figyelmet azért is, mert olyan rendkívül gazdag anyag a fejlődés térbeli koncepciók fejlődésének térbeli képzelőerő az élő kapcsolat a szigorú logika, amely a lényege a geometria. Már a legalapvetőbb tényeket polyhedra igényel egy ilyen kapcsolat, ami kiderül, hogy nem túl könnyű. Még egy ilyen egyszerű tény, mint a metszéspontja az átlók a doboz egy ponton, erőfeszítést igényel képzelet, hogy világosan és szigorú bizonyíték.
Mi több, a poliéderek elejétől tanulmányozása szilárd geometria különböző didaktikai célokra. A poliéder kényelmesen viszonylagos helyzetét jelzik a vonalak és síkok az űrben, a jelek használata, amely bemutatja a párhuzamos és merőleges egyenesek és síkok az űrben. Illusztráció az első szilárd geometria tételei bizonyos modellek javítja a diákok érdeklődését a téma iránt.
Ez is az egyik legfontosabb feladat a matematikát tanítani, hogy dolgozzon absztrakt gondolkodás a diákok. Ezt a célt jelentősen hozzájárul a használata a vizuális segédeszközök, és nem csak az alsó tagozatban, hanem az idősek. Lehetőségek a megvalósítása a cél ad a témája a „Polyhedra”, különösen a független produkciós hallgatók vizuális segédeszközök. A gyártási folyamat során poliéder modell, kivéve az elméleti ismeretek és készségek, a diákok rögzített formában az új fogalmak segítségével a rajz és a tényleges megoldása építési problémák. Az önálló gyártási modell kép jön létre részben fogva őket végezhet a különböző manipulációk. Az összes tulajdonságai és jellemzői könnyen elsajátítható és rögzítve van a memóriában a diákok.
Polyhedron - a geometriai test határolt minden oldalról sík sokszög úgynevezett arcok.
Hand élek - a széleit a poliéder, és a végén a bordák - csúcsai a poliéder. Szerint a nézőpont megkülönböztetni tetraéder, ötszög, és így tovább. D.
A poliéder konvex, ha minden egyik oldalán helyezkedik el a gépet. minden egyes arcokat.
Egy konvex poliéder nevezzük szabályos, ha annak minden arcok - ugyanazon szabályos sokszögek konvergál azonos élek számát, és a szomszédos arcok egyforma szögekben minden csúcs.
Az ábrán egy tetraéder, kocka, oktaéder, dodekaéder és ikozaéder. Alakjuk - a modell a tökéletesség! És miért rendszeres poliéder van ilyen név? Mi tulajdonságok birtokában vannak? Hogyan készítsünk egy modell egy szabályos poliéder? Ahol találkozhat ezekkel a csodálatos testet?
A választ ezekre a kérdésekre: a célja ennek a munkának.
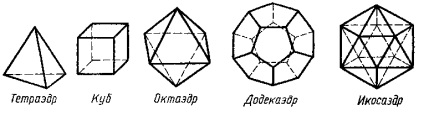
Minden szabályos poliéderek eltérő számú arcokat és neveket kapott ezt a számot.
Tetraéder (tetra. „- négy és görög HEDRA.” - arc) alkotja 4 egyenlő oldalú háromszög, 3 borda konvergálnak minden csúcshoz.
Kocka (a görög hexa. „- és hat HEDRA.” - kötött) 6 négyzet arcok, szélek 3 közelednek mindegyikébe a felső.
Kocka jobban ismert, mint a kocka (a latin cubus. „A görög kubos.”.
Oktaéder (a görög OKgombot - nyolc és HEDRA - arc) nyolc arcok (háromszög), az egyes felső 4 borda Converge.
Dodekaéder (a görög dodeka - tizenkét és HEDRA - arc) 12 metszettel (ötszögletű) minden egyes csúcsa a borda konvergálnak 3.
Ikozaéder (a görög eikosi - húsz és HEDRA - arc) 20 metszettel (háromszög), minden egyes csúcsa 5 élek. (5 s.267-269)
Kiderült, hogy a rendszeres polyhedra pontosan öt - se több, se kevesebb. Mivel annak érdekében, hogy valamilyen rendszeres poliéder minden vertex, az ő meghatározása, meg kell felelnie az arcok számát, amelyek mindegyike szabályos sokszög.
Összeg sík szöge polihidrális szög legyen kisebb, mint körülbelül 360. különben nem sokoldalú felület nem fog működni. Megy keresztül lehetséges egész megoldását egyenlőtlenségek: 60K
Rendszeres poliéderek körülöttünk.
A könyvben a német biológus század elején, Haeckel „Kunstformen der Natur”, akkor olvassa el az alábbi sorokat: „A természet táplálja saját kebelén kimeríthetetlen számú csodálatos lények, hogy a szépség és a különféle messze felülmúlja az összes teremtett emberi művészeti formák.” Így például, egysejtűek phaeodarians alakúak ikozaéder.
Egy másik érdekes tény, hogy ez egy ikozaéder lett a figyelem középpontjába biológusok vitáik, hogy a forma vírusok. A vírus nem lehet tökéletesen kerek, mint korábban gondolták. Telepítéséhez formájában, hogy a különböző poliéderek, irányított fény rájuk szöge mindig ugyanaz, mint az áramlás atomok a vírus. Kiderült, hogy csak az egyik poliéder adja pontosan ugyanolyan árnyalatú - ikozaéder. Ő geometriai tulajdonságok, mint már említettük, lehetővé teszi, hogy mentse a genetikai információt. Rendszeres poliéderek - a legkedvezőbb alak. És a természete ennek széles körű alkalmazása. A kristályok néhány ismerős anyagok formájában rendszeres poliéderek. Így a köbös kristály alakja továbbítja sót NaCi, egykristály alumínium-kálium-timsó az alakja egy oktaéder, kén-pirit FeS kristály alakja egy dodekaéder, surmenisty nátrium-szulfát - tetraéder, bór - ikozaéder.
Ha alkalmazzuk a zsebébe a világon a legnagyobb és legjelentősebb kultúrák és civilizációk az ókori világ, akkor észre egy mintát a saját pozícióját a földrajzi sarkok és az Egyenlítő a bolygón. Sok ásványi lerakódások mentén húzódnak ikosaedrovo-dodekaedrovoy rács. Meglepő dolgok történnek a kereszteződésekben ezen élek: itt található a központ az ősi kultúrák és civilizációk, Peru, Észak-Mongólia, Haiti, Ob kultúra és mások. Ezeken a pontokon a megfigyelt legnagyobb és legkisebb a légköri nyomás, óriás óceánok kavarog, itt skót Loch, Bermuda háromszög. További vizsgálatok a Föld meghatározhatja a hozzáállás, hogy ezt a szép tudományos hipotézis, amely, mint látható, a rendszeres poliéderek fontos helyük van. (2, 2)
A kutatómunka volt változatos és izgalmas, hogy megértsék, hogy a körülöttünk lévő világ törvényei alá tartoznak a geometria.
Ennek része a szakirodalomban vizsgálták a dolgozat a témában, sajátosságai a rendszeres poliéderek készült rajzok, szkennelés, modell, szabályos poliéderek.
A poliéder a háromdimenziós térben, a készlet egy véges számú sík poligonok, úgy, hogy minden oldalon az egyes sokszögek egyidejűleg a másik fél (de csak egy), az úgynevezett szomszédos az első (ezen az oldalon); minden a poligonok alkotó poliéder. Sétálhatunk ezek közül bármelyik, majd a vele szomszédos, és ez viszont, - .. a szomszédos, stb Ezek sokszögek nevezzük arcukat, fél - élek, és csúcsa - csúcsai a poliéder.
A világ tele van a szimmetria. Ősidők óta, ez jár a mi elképzelésünk a szépség. Talán ez annak köszönhető, hogy az elpusztíthatatlan ember érdeke, hogy a rendszeres poliéder - a csodálatos karakterek szimmetria, hogy felkeltette a figyelmét a sok neves gondolkodók Platón és Euclid Euler és Cauchy.
Az alakja a fő eleme a Föld - a kocka, a levegő - oktaéder Fire - a tetraéder, Víz - a ikozaéder, és az alkotó a világ adott formában ötszögű dodekaéder. Az a tény, hogy a Föld gömb alakú, a püthagoreusok tanított. Szerint Püthagorasz, van 5 db testi: magasabb isten univerzum is épül alapján a geometriai alakzat egy dodekaéder. A föld, mint az univerzum, Plato Föld - szintén dodekaéder.
Görög matematika, ami először poliéderek elmélete alatt fejlődött nagy hatással a híres filozófus Platón.
Plato (427-347 BC) - a nagy görög filozófus, alapítója az Akadémia és az alapító a hagyomány platonizmus. Az egyik alapvető jellemzője a tanítást, hogy fontolja meg az ideális tárgyak - absztrakciók. Matematika, elfogadása az ötleteket Platón óta Euclid tanult elméleti ideális tárgyakat. Azonban Platón maga, és számos ősi matematika fektetett távon ideális nem csak elvont értelemben, hanem azt jelenti, hogy a legjobb. A hagyományoknak megfelelően megy vissza a régi matematikusok közül a legjobb az összes poliéderek azok, akiknek az arcuk szabályos sokszög.
Az elmélet a poliéderek - az egyik izgalmas és vibráló terület a matematika. A jelen tanulmányban csak úgy tekintették, egy része ezt az elméletet. A rendszeres poliéder - a platóni testek - kaphatnak az úgynevezett félig szabályos poliéderek archimédeszi szilárd, az arcok, amelyek szintén helyes, de ellentétes sokszögek és a csillag jobb testet.
1.Dorofeev GV Peterson LG Matematika. 6. osztály. 3. rész - M: Balass 1988.