Milyen párhuzamossági jelek mutatják az iskolát?

1 jellemző.
Ha két oldal egyenlő és párhuzamos egy négyszögben, akkor ez a négyszög egy parallelogram.

Adott: ABCD, AD║ BC, AD = BC.
Bizonyítsd: ABCD - parallelogram.
bizonyíték:
A BD-t fogjuk rajzolni.
BC = AD hipotézis szerint,
∠1 = ∠2, mivel keresztben fekszik a szekant BD keresztmetszetén, az AD║BC,
A BD az ABD és a CDB háromszögek közös oldala, ⇒
ΔABD = ΔCDB két oldalán és a szög közöttük.
A háromszög egyenlőségéből következik
∠3 = ∠4, és ezek keresztirányú szögek a szekant BD egyenes vonalainak CD és AB metszéspontjához, majd
CD║AB.
Ha az ellenkező oldalak párhuzamosak a négyszögben, akkor ez egy paralelogramma.

2 jellemző.
Ha az ellenkező oldalak egyenlőek a négyszögben, akkor ez a négyszög egy parallelogram.
Adott: ABCD, AB = CD, BC = AD.
Bizonyítsd: ABCD - parallelogram.
bizonyíték:
A BD-t fogjuk rajzolni.
BC = AD hipotézis szerint,
AB = CD állapot,
A BD az ABD és a CDB háromszögek közös oldala, ⇒
ΔABD = ΔCDB három oldalán.
A háromszög egyenlőségéből következik
∠1 = ∠2, és ezek keresztirányú szögek a szekant BD BC és AD vonalak metszéspontjához, így a BC║AD és az ABCD egy parallelogramma az első jellemzőben.

3 jellemzőkkel.
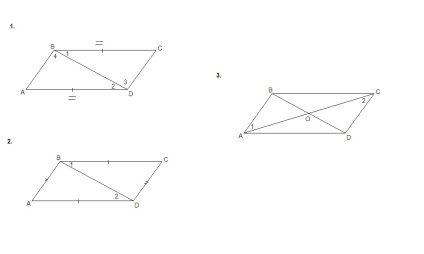
Ha egy négyszögben az átló átlója metszésponttal van felosztva, akkor ez a négyszög párhuzamos.
Adott: ABCD, AC∩BD = O, AO = OC, BO = OD.
Bizonyítsd: ABCD - parallelogram.
bizonyíték:
AO = OC hipotézissel,
BO = OD hipotézis szerint,
∠AOV = ∠COD függőleges, ⇒
ΔАОВ = ΔCOD két oldalán és a szög közöttük.
Ez azt jelenti, hogy AB = CD és ∠1 = ∠2, és ezek keresztirányú szögek a szekant AC AB és CD vonalainak metszéspontjához, tehát AB║CD.
ABCD - paralelogramma az első jelen.