Funkció y sinx, ee tulajdonságok és grafikon

Funkció y = sinx, ee tulajdonságok és grafikon

Az y = sin X függvény.

A 20. §-ban megfogalmaztunk egy szabályt, amely lehetővé teszi, hogy minden t szám megfeleljen a cos t számnak, azaz. az y = sin t funkciót jellemeztük. Megjegyezzük néhány tulajdonságát.

A függvény tulajdonságai u = sin t.

Tulajdonság 1. A meghatározás területe a valódi számok készlete.

Ez abból következik, hogy bármelyik 2-es számhoz a számkörön egy M (1) pont tartozik, amely jól definiált ordinátával rendelkezik; ez az ordinátum cos t.

Tulajdonság 2. u = sin t egy furcsa funkció.

Ez abból a tényből következik, hogy - amint azt a 19. § bizonyítja - minden egyenlőségre
Tehát az u = sin t függvény grafikonja bármely furcsa függvény grafikonaként szimmetrikus a tOu téglalap alakú koordinátarendszer eredetére vonatkoztatva.

Tulajdonság 3. Az u = sin t függvény növekszik az intervallumon
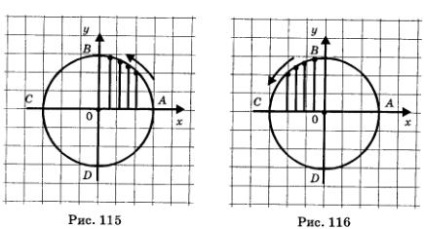
Ez abból a tényből következik, hogy a pont az első negyedében a numerikus ordináta kerülete fokozatosan növekszik (0-1 - lásd 115. ábra ..), és az ordináta fokozatosan csökken (1-0 pontként mozgását a második negyedévben numerikus kerülete - cm. ábra. 116).

Tulajdonság 4. Az u = sin t függvény alulról és felülről van határolva. Ez abból következik, hogy - amint azt a 19. §-ban láttuk - az egyenlőtlenség bármelyikét illetően

Tulajdonság 5. (Ez az érték eléri a funkciót az űrlap bármely pontján (ez az érték eljut az űrlap bármely pontjára
A kapott tulajdonságok felhasználásával megteremtjük a számunkra érdekes funkció grafikáját. De (figyelem!) Az u - sin t helyett írunk y = sin x (végül is megszoktuk az y = f (x), és nem u = f (t) írást). Ezért is építünk egy grafikont az ismert xOy koordináta rendszerben (a tOy helyett).
Összeállítunk egy táblázatot az y = sin x függvény értékeiről:

Megjegyzés. Itt van a "szin" kifejezés eredetének egy változata. Latinul sinus jelentése hajlítás (íjszál). A kialakított gráf bizonyos mértékig indokolttá teszi ezt a terminológiát.

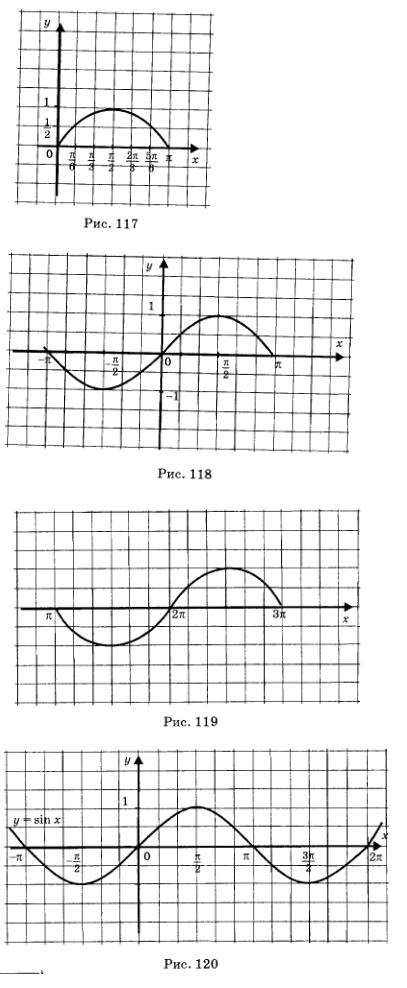
Az y = sin x függvény grafikonjaként szolgáló vonal neve sinusoid. A szinuszos rész, amely a 3. ábrán látható. 118-as vagy 119-es sávot szinuszos hullámnak nevezünk, és a szinuszos résznek, amelyet a 2. ábrán mutatunk be. 117, félhullámnak vagy szinuszos ívnek nevezik.

AG Mordkovich Algebra osztály 10

Ha bármilyen korrekció vagy javaslata van ehhez a leckéhez, írjon nekünk.

Ha látni szeretné a leckék más módosításait és kívánságait, nézze meg itt - Oktatási Fórum.