Fibonacci - előrejelzések és jóslás
A történelem az aranymetszés tartozó név matematikus Leonardo Pisa, az úgynevezett Fibonacci nevét. Ő volt a banner-nitym matematikus a középkorban.
1202-ben jött a közzétételének munkáját „The Book of Abacus” (a számlálás board), ahol minden időpontjában ismert a probléma, köztük egy nagyon szórakoztató feladat a nyulak gyűjtöttünk. A példa az élővilág ő világosan megmagyarázza, hogy mi van a Fibonacci-sorozat. Itt látható az állapota.
„Valaki egy pár nyúl egy olyan helyen, bekerített minden oldalról a fal, hogy megtudja, hány pár nyúl születik egy időben az év során, ha a természet nyulak, hogy egy hónap után a pár nyúl szül egy másik pár, és szülni nyulaknak a második hónapban születése után. "
Mivel az első pár nyúl - újszülöttek, majd a második hónapban, akkor nem teszi lehetővé az utód, és az is marad egy pár. A harmadik hónapban termelnek egy pár 1 + 1 = 2. A negyedik hónapjában két pár mag csak egy pár (a második még megakadályozza a alom): 2 + 1 = 3 pár. Az ötödik hónapban született két pár harmadik hónap így az utódok: 3 + 2 = 5 par. A hatodik hónapban az utódok csak akkor azok a párok, akik született a negyedik hónapban: 5 + 3 = 8 pár, stb ...
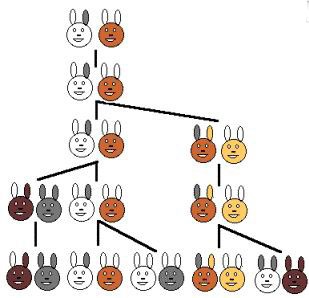
Reflektálva egy hasonló jelenség, Fibonacci adta a következő számsorozat.
Így, mert ez a probléma jelenik meg következetes mintát, és ezek a számok alkotnak egy jól ismert szekvenciája 1, 1, 2, 3, 5. 8, 13, 21, 34. 55. 89. 144. 233. magukat számok nevezzük Fibonacci számok, és azok szekvenciát - a Fibonacci-sorozat.
Egészen egyszerűen, mint minden nagyszerű. Mi az értelme ennek a sorozatot?
Kiderült, hogy minden tagja a harmadik, egyenlő az összege az előző két 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13 + 21 = 34 és r. D., és az arány a szomszédos számok a sorozat megközelíti a viszonyát az arany Division. Ez jelöli a görög betű „phi” - F, és van úgy, hogy egyenlő 1.618.
Ez ad folyamatos körzet egy vonalszakasz a aranymetszés, növekvő vagy csökkenő ez a végtelenbe, amikor a kisebb szegmens utal, hogy a olyan nagy, mivel több mindent.
Ez az érték Luca Pacioli úgynevezett isteni arányban. Úgy is nevezik, az arany arány, arany átlagos, aranymetszés. Azaz, ez az arány az egyik a „kincsek” a geometria.
Ez még nem minden. Amikor a szétválás a bármely tagja a Fibonacci-sorozat következő kiderül kölcsönös fi (1: 1,618 = 0,618). Ez a figyelemre méltó jelenség, mert az is végtelen.
Ha elosztja az egyes számot azt követő keresztül kapott 0.382.
Így, hogy egy központi, sor Fibonacci arányok: 4,235. 2,618, 1,618, 0,618, 0,382, 0,236, amely különleges szerepet játszhat szabályozásában jellegű.
Fibonacci-sorozat maradt volna csupán egy matematikai casus ha a kutatók a növény- és állatvilág, valamint a művészetek mindig nem jött el ez a sorozat, mint egy aritmetikai kifejezést a törvény az arany részlege.
Hangsúlyozni kell, hogy a ragyogó Fibonacci csak megfogalmazott és így, ahogy azt emlékeztetett emberiség arany szekvenciát, amit ismert, mint az arany osztály az ősi időkben. Elképesztő, hogy a Fibonacci-sorozat látható az élővilágban. Atom maga „beépített” elve alapján az aranymetszés. Ez az elv a legtöbb, ha nem az összes területeken a modern tudomány.
Az az elképzelés, az aranymetszés kiegészíti a spirál nagyon gyakori a természetben. Spirálisan hullámos mosogató tanult Archimedes és magával hozta az egyenletet. Spirál húzott ebből az egyenletből, róla nevezték el. Növelte pályán mindig egyenletesen. Jelenleg, a spirál Arkhimédész széles körben használják a szakterületen.
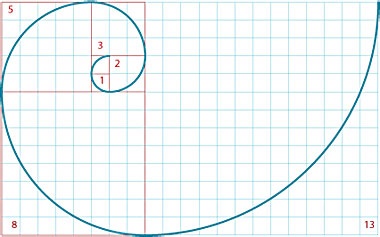
Sok természetes folyamatok fejlődnek azt egy spirál. Például, a hóvihar forog hó tömegek mentén spirálok, hurrikánok keletkeznek és unwinds is spirálisan. Közös pók szövi a web egy spirál. Rémült állomány rénszarvas szétszórt spirál. Kettős spirál DNS-molekula csavart. Goethe úgynevezett spirális „élet görbe”. Az ágak fa levelei nem nőnek véletlenszerűen spirálisan a spirál irányát. Spirál egyértelműen látszik a megállapodás a napraforgómag.
Közös kutatási botanikusok és matematikusok megvilágítani ezt a csodálatos jelenséget. Kiderült, hogy a megállapodás a levelek egy ág, napraforgómag, fenyőtoboz bizonyítja a Fibonacci-sorozat, ami azt jelenti, hogy a törvény az aranymetszés. Ananász és a kaktusz is elvét megtestesítő az aranymetszés.
Ezek a minták láthatók az energia átmenetek az elemi részecskék a szerkezet a kémiai vegyületek, bolygómű és a űrrendszereket génszerkezetek az élő szervezetek, a szerkezete egyedi szervek és emberi szervezet egészére hanem bioritmus és az agy működő vizuális érzékelés.