Diszkrét matematika algoritmusok
Emlékezzünk az alapvető definíciók gráfelmélet. Legyen V egy nem üres véges halmaz. Keresztül V (2) a készlet két-elemű részhalmazát V. Egy gráf egy pár készletek (V. E), ahol E - tetszőleges részhalmaza V (2). Az elemek a készletek V, illetve E nevű csúcsok és az élek a gráf G gráf (V. E) az úgynevezett teljes. Ha bármely két csúcs össze van kötve a legalább egy irányban.
Útvonal (vagy) a gráf G a fent említett váltakozó sorozata csúcsok és az élek 0. v e v 1. 1. ..., v t -1. E T. v t +1. ahol e i = v i -1 V I (1 ≤ i ≤ t). Egy ilyen útvonal röviden említett (V 0. V t) -marshrutom, és azt mondják, hogy ez összeköti v 0 C V t; viszont a csúcsai a v 0. V t - a felső végén ezen az útvonalon. Az útvonal hossza hívják az élek számát tartalmazza azt. Megjegyezzük, hogy egy közönséges gráf szekvenciát teljesen határozza meg az útvonal v 0. v 1. ..., V t a csúcsok. Ha v 0 = V t. majd (v 0. v t) -marshrut úgynevezett zárt.
Lánc - Egy út nem ismétlődő élek. A lánc az úgynevezett egyszerű láncot, ha nem ismétli csúcsot kivéve talán egybeeső végén csúcsot. Zárt egyszerű áramkör úgynevezett hurok (vagy hurok).
Lánc Hamilton gráf egyszerű áramkör, amely áthalad minden csúcsa a grafikon pontosan egyszer. Cycle Count áthaladó minden csúcsot nevezik Hamilton kör. Egy gráf Hamilton. ha van egy Hamilton-kör.
Ezek a nevek a láncok és a ciklusok nevéhez William Hamilton (Hamilton W.), aki 1859-ben a következőket javasolta a kirakós játék, hogy szükség van az elhaladó felváltva az egyik csúcs másik csúcsa a dodekaéder azon a szélén, hogy megkerülje mind a 20 csúcsot egyszer visszatér az eredeti csúcs.
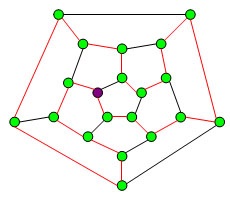
Megjegyezzük, hogy feltalálták sok más szórakoztató és hasznos feladatokat látnak el a keresést Hamilton-kör. Fogalmazza ketten.
- (A probléma a lakoma), a vállalat több ember kell, hogy üljön a kerekasztal oly módon, hogy mindkét oldalán minden barátai voltak. Nyilvánvaló, hogy megoldja ezt a problémát, meg kell találni a Hamilton-kör a gráfban társkereső cég.
- (A probléma a sakk ló.) Lehet, kezdve egy tetszőleges mező egy sakktábla, hogy megkerüljék a ló következetesen mind a 64 mező egyszer, és visszatér az eredeti területen? (Ahhoz, hogy az alábbiakban tárgyaljuk).
A következő tétel bizonyítása Pausch (Posa L.), ad elégséges feltétele egy irányítatlan gráf Hamilton. Ez összefoglaljuk a kapott eredményeket a korábban Ore (Ore O.) és Dirac (Dirac G. A.), amely publikációkat a továbbiakban következtében.
Legyen G egy p ≥ 3 csúcsot. Ha minden n. 1 ≤ n ≤ (p-1) / 2, a csúcsok száma és mértéke nem haladja meg a n. kevesebb, mint n. és egy páratlan számú fokozatot p csúcsok (p-1) / 2-nél nem nagyobb (p-1) / 2, akkor a G - Hamilton grafikon.
Bizonyítás. Tegyük fel, hogy a tétel hamis, és hagyja, hogy a G - a maximális nem-Hamilton gráf p csúcsok, kielégíti a feltételeket, a tétel. Könnyen látható, hogy a felül bármely él a gráfban tulajdonságokkal rendelkező meghatározott tétel vezet a grafikon, ami ugyanaz rendelkezik ezekkel a tulajdonságokkal. Így, mivel a hozzáadott G tetszőleges szélén vezet Hamilton grafikon, bármely két nem szomszédos csúcsot csatlakozott egyszerű szélességméret (amely tartalmazza az összes a gráf) lánc.
Először azt mutatják, hogy minden csúcsa, a mértéke, amely nem kevesebb, mint (p-1) / 2, szomszédos minden csúcs a nél nagyobb fokú (p-1) / 2. Tegyük fel (az általánosság elvesztése nélkül), hogy a C v 1 ≥ (p-1) / 2 és C v p ≥ p / 2, de a vertex v 1 és v p nem szomszédosak. Aztán van egy egyszerű feszít®fája lánc v 1 v 2, ... v o. összekötő v 1 és v o.
Jelöljük vertex szomszédos v 1. keresztül v i 1, ..., v i n. ahol n = deg v 1 2 = i 1 v 1 v 2 ... v i j v o v -1 p -1 ... V I j v 1.
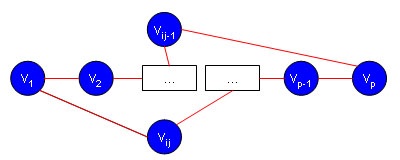
Továbbá, mivel n ≥ (p-1) / 2, akkor p / 2 ≤ ° v p ≤ p -1- n
Ebből következik, hogy ha a C v ≥ p / 2 minden csúcsok v. A G - Hamilton grafikon. (Itt van megfogalmazva formájában Corollárium 2) Tekintettel a fenti, mindegyik pár szomszédos a gráf G, azaz G - teljes gráf. Van egy ellentmondás, hiszen egy teljes gráf Hamilton minden p ≤ 3.
Így, G - v egy csúcsból ° v
Adott egy elégséges feltétel nem szükséges. Cubic grafikon az ábrán látható, Hamilton, bár nyilvánvaló, hogy nem felel meg az a tétel. Azonban a feltételeket, a tétel nem lehet javítani, mert a gyengülő új állapot nem lesz elegendő egy Hamilton-gráf.
Pausch korlátozó feltételeket, a tétel, megkapjuk az egyszerűbb, de kevésbé erős elégséges feltételt talált Dirac és Ore rendre:
Következmény 1
Ha p ≥ 3 és C u + ° v ≥ p bármely két u és v értéke nem szomszédos csúcsai G. akkor G - Hamilton grafikon.
Következmény 2
Ha p> és 3 ° v ≥ p / 2 minden v csúcs a gráf G - Hamilton grafikon.
A teljes gráf G (V E) mindig van egy Hamilton út.
Bizonyítás. Legyen m = 1, 2 ... p - hosszúságú út p -1, ahol az összes csúcs m különböző. X - a tetején ∉ m. Megmutatjuk, hogy lehetséges, hogy az utat a forma
Tegyük fel, nincs ilyen egész szám k. lépett az 1 és p. hogy
Van tehát, hogy 1 ≤ k ≤ p.
(A k. X) ∈ E → (x. A k + 1) ∉ E → (a K + 1. X) ∈ E.
Ha nincs útvonal, M 0 = x 1 ... a o. akkor (a 1 x) ∈ E → (a 2. x) ∈ E. (p. x) ∈ E. útvonalat, és m p = 1 ... p x létezik, ellentétben a feltételezést. Így tudjuk lépésről lépésre építeni az utat tartalmazza az összes a gráf. ♦
Megjegyzés. Ez az eredmény azt jelenti, hogy mindig lehet rendelni egy csomó játékos a torna, hogy minden az előző volt a győztes után azonnal (kivéve persze, sem a találkozók nem döntetlen).
A probléma a sakk ló
Mi jelent a probléma, hogy kb ló sakktábla, hogy látogatása minden sejt pontosan egyszer. Ez a probléma iránt érdeklődő sok matematikus, különösen Euler (Euler L.), de Moivre (de Moivres) Vandermonde (Vandermonde), és mások.
A szabály, amely, úgy tűnik, indokolt a gyakorlatban, de elméletileg még nem erősítették meg a következő: minden alkalommal megyünk ló vissza, ahol ez veszélyezteti a legkisebb számú még nem telt el a sejteket.
Egy másik módja az, hogy talál egy útvonalat a félpanzió, szimmetrikus kettős, és a kapcsolat mindkét utat.
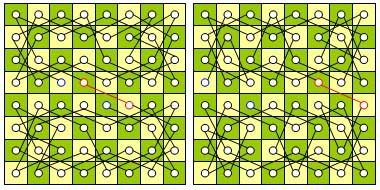
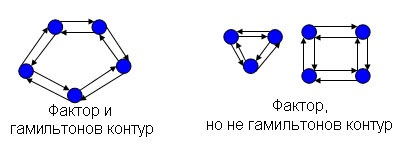
Factor grafikon (V. E) nevezik részleges grafikon (V. E 0), ahol minden csúcs van outdegree és beállítási értéke 1. Minden Hamilton út egy tényező, de a fordítottja nem igaz, hiszen a faktor állhat több áramkör nincs közös csúcsok .
EA = ∪ u ∈ A Eu.
azaz EA egy kép több csúcsnál
Adjuk meg egy egyszerű gráf (V. V * E.), ennek megfelelő tetszőleges gráf (V. E), a következők szerint: V * a duplikátuma a beállított V. av * k ∈ Ev i (V. V * E.) akkor és csak akkor amikor vk ∈ Ev i (V. E).
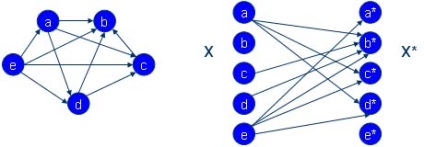
3. Tétel (Koenig-Hall (Konig D. Hall-P.))
Megfelelő, térképek V USP létezik akkor és csak akkor, ha | EW | ≥ | W | bármely beállított W ⊂ V.
Legyen (V. U. E) - egy egyszerű gráf, egy
Aztán ott van mindig a megfelelő, felhasználva az összes csúcsot v. hogy | ev | = M. és mindazoknak, akik csúcsot u. hogy | E -1 u | = M.
A szükséges és elégséges feltétele, hogy létezik egy faktor gráf (V. E) az, hogy | EW | ≥ | W | amikor az összes W ⊂ V.
Bizonyítás. Valóban, 3. tétel, ez a feltétel azt fejezi ki, hogy egy egyszerű gráf (V. V *. E), van egy párja, térképek V V *. ♦
Ha a gráf (V. E) úgy, hogy | ev | = | E -1 v | = M bármilyen vertex v. Az íven a grafikonon osztható m diszjunkt W 1 W 2 ..., Wm. amelyek mindegyike képez tényező.
Bizonyítás. Egyszerű gráf (. V. V * E) az a tulajdonsága | ev | = M. | E -1 v * | = M. A következmény a 3. Tétel lehet térképezni, hogy V V * és ezáltal meghatározzák W 1. A részleges grafikon eltávolítása után marad ívek 1. W lehet megjeleníteni V V * és ezáltal meghatározzák W 2, stb ♦
Megtalálása faktor egy egyszerű dolog, mert ez a probléma a maximális áramlás. Eljárás találjanak Hamilton út áll a megállapítás a tényezők a grafikonon, és megtartása csak azok, amelyek tartalmaznak egy ciklust.
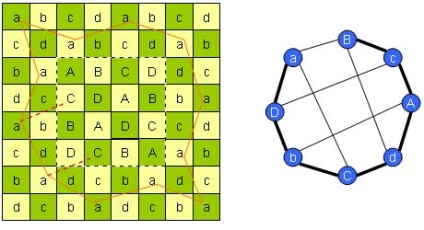
Akkor „ragasztó” kontúrok tényező. Tekintsük ismét a problémát, hogy egy sakk ló. Mivel a szimmetria faktor kapott sakktábla az ábrán feltüntetjük. A sejteket jelölt azonos betűvel hurkot alkosson. A két áramkör kombinálhatjuk, ha, és csak akkor, ha a két egymást követő csúcsok rendre szomszédos két szomszédos csúcsa a másik. Különböző csatlakozások láthatók segítségével a kiegészítő grafikon. Kiegészítő grafikon nyilvánvaló Hamilton út aDbCdAcB.
Az algoritmus találni egy Hamilton-kör
Vegyünk egy rekurzív függvény searchHamiltonianCycle. ami igazat ad vissza. Ha a gráf Hamilton, és egyébként false.
- numberOfVertices - a csúcsok száma a grafikonon
- v - az utolsó talált a csúcs
- w - a kezdeti csúcs (keresés kezdődik meg)
- d - A fennmaradó hossza Hamilton kör
Ez az algoritmus hasonlít az algoritmus a keresési mélységben (DFS). A fő különbség a pirossal jelzett:
- függvény megkapja a kezdeti csúcs w, és a hosszúsága Hamilton kör, mint a második és a harmadik paraméter, illetve;
- 1. sorban, a művelet ellenőrzi, hogy az összes csúcsot már meglátogatott (d == 1), és ha igen, van-e egy peremmel, amely a csúcs a start végét. Ha mindkét feltétel teljesül, a Hamilton-kör található;
- 7. sor, a funkció visszaállítja az érték a marker látogatták meg. mielőtt visszatér az érték, ami azt jelenti, hiba.
Rekurzív keresés Hamilton kör előírhatja exponenciális időt.
Bizonyítás. Tekintsük a grafikon egy csúcsot elkülönítjük, és a széleket, hogy csatlakoztassa a többi | V | -1 csomópontok alkotnak teljes gráf. searchHamiltonianCycle funkció soha nem fog találni egy Hamilton-kör, de feltárja az összes (| V | -2)! utak kezdve a kiválasztott elsődleges csúcsok, amelyek mindegyike használ | V | -1 rekurzív hívások. Következésképpen, a teljes száma rekurzív hívások egyenlő (V-1). ♦