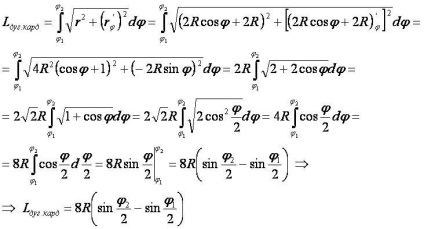A kardioidok ívhossza
A kardioid ívhossza olyan szám, amely a kardioid ív hosszát hossza egységében jellemzi.
A kardioid egy vonal, amelyet egy kör pontja ír le, amikor az utóbbi egy ugyanazon sugarú kör mentén csúsztatva csúszik.
Úgy tűnik, hogy egy gördülő kör keletkezik.
Vegyük figyelembe a kardioidok ívét -π≤φ≤π.
[szerkesztés] Legend
x1 az ív első pontjának abszcisza;
y1 - az ív első pontjának koordinátája;
φ1 - az ív első pontjának szöge (kisebb);
x2 az ív második pontjának abszcissza;
y2 az ív második pontjának koordinátája;
φ2 az ív második pontjának szöge (nagyobb);
R a generáló kör sugara;
φ független változó;
r = 2R (1 + cosφ) - a kardioid egyenlete a poláris koordinátákban;
t egy paraméteres változó;
x = 2Rcost (1 + költség) - az abszcissza cardioidok paraméteres egyenlete;
y = 2Rsint (1 + költség) - a kardioid ordinátájának paraméteres egyenlete;
Lug.kard - a kardioid ívhossza.
[szerkesztés] A képlet
[math] L_ \ text = 8R \ bal (\ sin \ frac- \ sin \ frac \ right), \ - \ pi \ le \ varphi_1 \ le \ varphi_2 \ le \ pi [/ math]- A teljes (a-tól-ig) kardioid hossza megegyezik a Lkard = 16R gyártási kör 16 sugaraival.
[szerkesztés] A képlet származéka