Részletes euklideszi algoritmus - Oldal Mikhail Medvedev
Algoritmust a legnagyobb közös osztója (GCD) indult, és a görög matematikus algoritmus az úgynevezett „kölcsönös kivonás.” Bár említést az algoritmus még Arisztotelész, később vált ismertté, mint az euklideszi algoritmus. Mi a legnagyobb közös osztó, tulajdonságai és számítási módszerek tárgyalja [1].
Emlékezzünk, hogy a legnagyobb közös osztója a két szám alapján lehet kiszámítani, hogy a következő kiújulásának:
C nyelv számítási eljárást GCD jelentése:
int GCD (int a, int b)
ha (b == 0) vissza;
vissza GCD (b, a% b);
Euklideszi algoritmus lehet terjeszteni, hogy meghatározza a megállapítás a és b egészek x és y. hogy ax + by = d. ahol d - a legnagyobb közös osztó és b.
Ezután az értékek az x és y. amelyek megoldásai az egyenlete ax + by = d. a kapcsolatok
x = y 'y = x' - y „· (2)
Miután kifejezésen egész részét a / b.
Bizonyítás. Ennek mod b = a - b ·. az
d = x '· b + y' · (a - · b) = y '· a + (x' - y „·) · b = x · a + y · b,
ott, ahol az x = y 'y = x' - y „·.
gcdext funkció (int a. int b. int * d. int * x. int * y), az alábbiakban, a bemeneti és b számok jelentése D = GCD (a. b), és az ilyen x. y, hogy D = a · x + b · y. Ahhoz, hogy megtalálja az ismeretlen x és y kell futtatni rekurzívan gcdext funkciót (b. A mod b. D. X. Y), és újraszámítja az értékeket x és y a fenti adott képletet. A rekurzió végződik, amikor b = 0. Ha b = 0 lnko (a. 0) = A és a = a · 1 + 0 · 0, ezért feltételezzük, x = 1, y = 0.
void gcdext (int a, int b, int * d, int * x, int * y)
Manuális elvégzéséhez a kiterjesztett euklideszi algoritmus kényelmes a használata egy asztal négy oszlopot (amint azt az alábbi példában), a megfelelő értékének. b. x. y. Így a számítási eljárás három részre osztja:
a) Először számítsuk lnko (a. b), hogy az első két oszlopa az asztalra, és a kapcsolat (1). Az utolsó sor az oszlopban, és az érték kerül a d = GCD (a. B).
b) rögzíti a értékek 1 és 0, illetve X és Y oszlopban az utolsó sor.
c) Mi folyamatosan töltse sor oszlopok x és y alulról felfelé. Az x és y az utolsó sorban a már megadott a b) lépésben. Feltételezve, hogy az aktuális sor már ki van töltve értékeket (x „y”), használjuk a (2) képletű újraszámítja, és írni értékeket (x. Y) a megfelelő sejtvonal fölött álló.
1. Advanced euklideszi algoritmus. Azt találjuk, a megoldás a 5x + 3y = 1. kiszámítása a legnagyobb közös osztója (5, 3), és megállapította, a megfelelő x. y termelődik az alábbi táblázatban:
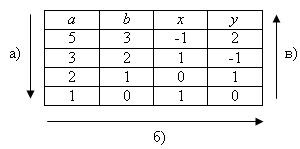
Sorrendje és iránya számítások nyilakkal jelzett és betűk.
A táblázat azt találjuk, hogy a GCD (5, 3) = 5 x (-1) + 3 · 2 = 1, azaz, ha x = -1, y = 2.
Vegyük például, az értékek az (x. Y) az első sor. A második sor veszi az értékeket (x 'y') = (1, -1). Képlet alapján (2), kapjuk:
y = x '- y' · = 1 - (-1) + = 1 + 1 = 2
Összehasonlítva az úgynevezett lineáris egyenlet formájában ax = b (mod n). Ez a megoldás akkor és csak akkor, ha b értéke osztható d = GCD (a. N). Amennyiben d> 1, az egyenlet lehet egyszerűsíteni helyette egy 'x = b' (mod n '), ahol A' = A / d. b „= b / d. n „= n / d. Az átalakítás után a „és n” kölcsönösen elsődleges.
Egy algoritmust megoldani egy egyenlet „x = b” (mod n „) a relatív prím a” és n „jelentése két részből áll:
1. egyenlet megoldásához egy 'x = 1 (mod n'). Ehhez a bővített euklideszi algoritmus keresik a megoldást (X0. Y0) egyenlet egy 'x + n' y = 1. Figyelembe modulo n 'utolsó egyenlőséget kapunk egy' x0 = 1 (mod n „).
Példa. Problémák egyenletet 18x = 6 (mod 8).
Az érték a d = GCD (18, 8) = 2 a térelválasztó 6, azonban van egy megoldás. Miután egyszerűsítése egyenletet kapjuk 9x = 3 (mod 4). A Lemma egyenértékű 3x = 1 (mod 4). Egyenlet megoldását 3x + 4y = 1 használva a kiterjesztett euklideszi algoritmus, azt kapjuk az x = -1, y = 1. Ha X = 1 (mod 4) = 3. Azaz, X = 3 lesz, mint egy oldatot 3x = 1 (mod 4 ) és 18x = 6 (mod 8).
Úgynevezett Diophantine egyenletek formájában
Ebben a részben figyelembe vesszük az algoritmus megoldásokat találjanak lineáris Diophantine egyenlet két ismeretlen a nyomtatvány egy · x + b · y = c (a továbbiakban az egyszerűség kedvéért, akkor kihagyja a szorzás jelek és levelet proto ax + by = c).
1. Tétel A egyenlete ax + by = c egész megoldása, ha, és csak akkor, ha a C osztható GCD (a. B).
Tétel 2. Ha a pár (X0. Y0) a megoldást a egyenlete ax + by = c. az egész készlet a megoldások (x y.) által leírt képlet:
Ahhoz, hogy megtalálja a részmegoldások (. X0 Y0) egyenlete ax + by = c először meg kell találni egy megoldást (x 'y') az egyenlete ax + by = d (d - a legnagyobb közös osztója a és b) felhasználásával a kiterjesztett euklideszi algoritmus, majd szorozza meg ac / d. tehát
Példa. Keresse meg a meghatározott megoldás az egyenlet 5x + 3y = 7.
1. Az egyenlet a megoldás, mivel a 7 elosztjuk a GCD (5, 3) = 1.
2. Find oldatot 5x '+ 3y' = 1 a kiterjesztett euklideszi algoritmus: (x 'y') = (-1, 2).
3. Keresse meg a megoldást (x0 y0.) Kiindulási Diophantine egyenlet:
Tétel szerint 2, a sor megoldást kiindulási Diophantine egyenlet formájában: