Arcsin (x) arcsin (-x)
Ahhoz, hogy egyszerűsítse a kifejezést arcsin (x) + arcsin (-x) vagy arctg (x) + arctg (-x), elég megjegyeznünk, csak egy tulajdonság az ív szinusz (arc tg).
arcsin (-x) = - arcsin (x), arctg (-x) = - arctg (x). ezért
arcsin (x) + arcsin (-x) = arcsin (x) -arcsin (x) = 0,
arctg (-x) + arctg (x) = 0.
tg (arcsin (x) + arcsin (-x)) = tg 0 = 0,
sin (arcsin (x) + arcsin (-x)) = sin 0 = 0,
cos (arcsin (x) + arcsin (-x)) = cos 0 = 1,
tg (arctg (-x) + arctg (X)) = tg 0 = 0,
sin (arctg (-x) + arctg (X)) = sin 0 = 0,
cos (arctg (-x) + arctg (x)) = cos 0 = 1.
Ha szükség van, hogy össze egy grafikon y = arcsin (-x) + arcsin (x), az oldatot kezdődik találni terület meghatározása.
A doménje Ez a funkció megegyezik a domain a funkció y = arcsin (x):
Így a függvény grafikonját y = arcsin (-x) + arcsin (x) csökkenti, hogy a grafikon lineáris függvény az y = 0, és olyan vonalat képvisel szegmenst feküdt a tengelyen Ox végpontokkal x = -1, és x = 1:
Grafikon függvény y = sin (arcsin (-x) + arcsin (x)) és y = tg (arcsin (-x) + arcsin (x)) is képviselik szegmensek x = -1, hogy x = 1, feküdt a tengelyen ökör. Bár, ha a második függvény meghatározása terén úgy vélik, hogy az érintő meghatározatlan pont
ezek bármelyike pont tartozik az intervallumot -1 és 1.
A grafikon y = cos (arcsin (-x) + arcsin (x)) - vonalszakasz y = 1, a végei az x = -1, és x = 1:
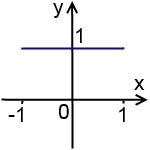
ARccOS (-x) = N-arccos (x), arcctg (-x) = N-arcctg (x). ezért
ARccOS (-x) + arccos (X) = N-arccos (x) + arccos (X) = N,
arcctg (-x) + arcctg (X) = N-arcctg (x) + arcctg (x) = AP
sin (ARccOS (-x) + arccos (X)) = sin n = 0,
cos (ARccOS (-x) + arccos (X)) = cos n = 1,
tg (ARccOS (-x) + arccos (X)) = tg n = 0,
sin (arcctg (-x) + arcctg (X)) = sin n = 0,
cos (arcctg (-x) + arcctg (X)) = cos n = 1,
tg (arcctg (-x) + arcctg (X)) = tg n = 0.
A domain a funkció y = arccos (-x) + arccos (x) -
Funkció gráf egy szegmens x = -1, hogy x = 1 - egy része a vonal y = n:
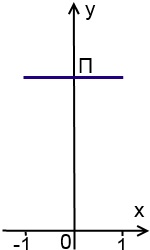
y = arccos (-x) + arccos (x)
A grafikon y = arcctg (-x) + arcctg (x) - y = n sor (ív kotangensét domén - az egész valós vonal):
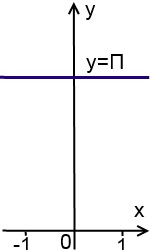
A grafikon y = tg (arctg (x) + arctg (-x)) - egyenes y = 0 (azaz, a tengely ox) kilyukadt X = P / 2 + Pn, ahol n - egész számok:
y = tg (arctg (x) + arctg (-x))
y = tg (arcctg (x) + arcctg (-x))
A grafikon y = tg (arcctg (x) + arcctg (-x)) - ugyanazon a vonalon.
Grafikon függvény y = sin (arctg (x) + arctg (-x)) és y = sin (arcctg (x) + arcctg (-x)) jelentenek közvetlen y = 0 (azaz, a tengely ox).
A grafikon y = CTG (arcctg (x) + arcctg (-x)) - egyenes y = 0 defektekkel