Megoldás és részletes elemzést cent feladatok fizikából 2018-ra

B1 feladat. Egy áthidaló teszi egy ugrás egy magassága h = 1200 m-rel a földfelszín nélkül kezdeti függőleges sebességét. Alatt az időtartam Δt1 = 6,0 c ejtőernyős szabadon esik, majd ejtıernyıs kinyitják és elhanyagolható ideig az ejtőernyős sebessége csökkent. További csökkentése ejtőernyős amíg touchdown történt állandó modulo függőleges sebesség v. Ha a mozgás-nyitó ejtőernyő alatt bekövetkezett időintervallum At2 = 92 c. függőleges sebességét modul v Ha ez a mozgás egyenlő ....
A szabadesés ejtőernyős nélkül kezdő függőleges sebességű repülés távolság:
Ha v - sebesség az ejtőernyős után ejtőernyő függvényében a távolságot, amelyet a skydiver repülő nyitott ejtőernyő, valamint:
Mivel ezek összege távolságok egyenlő a magasság, ahol egy ejtőernyős ugrott, majd
Ezért a kifejezett süllyedési sebesség a nyitó az ejtőernyő:
Helyettesítő számértékek:
B2 feladat. A vízszintes emeleten a lift, mozgó lefelé gyorsulás bőrönd tömege m = 30 kg, ami bázis területen S = 0,080 m 2. Amennyiben a nyomás által kifejtett bőröndöt a földre, p = 2,4 kPa, a gyorsulás modul egy felvonó ... .
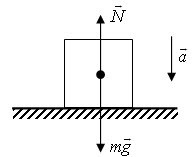
Tekintsük ható erők a bőröndbe. Ez a gravitációs erő és a padló reakció erő. Befolyása alatt ezeknek az erőknek a bőrönd mozog gyorsulás egyenlő a gyorsulás a lift és lefelé is.
Írjuk fel az egyenletet egy bőrönd Newton második törvényét:
Vetítjük az egyenlet a tengelyen Oy.
Floor reakció erő Newton harmadik megegyezik a súlya a bőrönd, amely megtalálható ismeretében a nyomás a bőröndöt a padlón a felvonó és lábnyom bőrönd:
Helyettesítő számértékek:
B3 feladat. A vízszintes egyenes szakasza száraz aszfaltút a vezető alkalmazta a vészféket. Brake a gépjármű útvonalának megáll alkotja s = 31 m. Ha a súrlódási együttható a kerekek között, és az aszfalt μ = 0,65, akkor a modul vezetési sebesség v0 elején a fékezési távolság azonos ....
Vészfékező a kerekek az autó le van tiltva, és elkezd csúszni az úton. Az autó, miközben a gravitáció és a padló reakció erő a súrlódást. Járműgyorsulási irányul az út mentén.
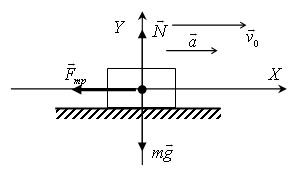
Írjuk fel az egyenletet az autó Newton második törvényét:
Vetítjük megadott egyenlet a koordinátarendszerben tengely:
A második egyenletből találunk támogatást reakciót :.
Ismerve a reakció támogatását, azt látjuk, a súrlódási erő a törvény száraz súrlódás:
Ezután a vetítés a gyorsulás az utazás:
A „-” jel azt jelzi, hogy a nyúlvány a gyorsulás irányul irányával ellentétes irányban a tengely Ox.
Megjegyzem, hogy a fenti rendszer közös problémák megoldására a dinamika. Persze, akkor is kap egy sokkal gyorsabb gyorsulás azonban bonyolultabb feladatok aprólékos vizsgálata erők, Newton második törvénye bejegyzés vektor formában és előrejelzések a koordinátatengelyeken teszi, hogy elkerüljék a hibákat. Ezen kívül mindig ajánlom az ismeretlen vektor nagysága (ebben az esetben a gyorsulás) mentén irányul pozitív irányt a koordináta tengelyeket -, akkor a jele az eredmény megmutatja az igazi irányt a vektor.
Tehát megtaláltuk a gyorsulás vetítés. A szerepe a dinamikáját. Ismerve a gyorsulás mozgás lehet kapcsolni a mozgás az autó, és a sebessége elején és végén az utazás:
Felhívjuk figyelmét, hogy az írott formula teszi pozíciója megváltozik (áthelyezés), de nem úgy, ahogy. Azonban, ha a test mozog egy egyenes vonal nélkül megfordulását, az elérési út elmozdulás.
Behelyettesítve ismert feljegyzett értékek a képletben, tekintettel arra, hogy V2x = 0 (a végén az útvonal az autó megállt):
Feladat B4. A sima felület a vízszintes sáv van m1 = tömege 52 g van a falhoz csatlakozik rugó merevsége súlytalan (lásd. Ábra.). Plasticine gyöngy m1 tömege = 78 g. Repülő vízszintes tengelye mentén a rugó sebességgel modul, amely belép a bár és tapad ahhoz. A maximális tömörítési a rugó | AL | Mindegy ... mm.
A probléma megoldódik két szakaszból áll: az első, a törvény lendületmegmaradás határozza meg a sebességet a bárban a labdát ragadt rá az ütközés után, majd a törvény az energiamegmaradás találunk tavasszal deformáció.
diákok gyakran kínálnak, hogy megoldja ezt a fajta probléma, csak a törvény az energiamegmaradás: kinetikus energia egyenlővé a beérkező labdát, és a potenciális energia az összenyomott rugó. Ez a megközelítés a baj! Az a tény, hogy a rugalmatlan ütközés mechanikai energiát nem konzervált - része hővé alakul, de a lendület megmarad akkor is, ha az ütközés rugalmatlan, ezért az ilyen problémákat meg kell oldani két szakaszban történik.
Így a vetülete a lendület az incidens labda a vízszintes tengelyen P1X = m2v. Let v1 - a sebességet a bár a ballon után a tapadás, akkor a vetülete a lendület a vízszintes tengely egyenlő: P2X = (m1 + m2) v 1.
A törvény alapján a lendületmegmaradás:
Most használd a törvény az energiamegmaradás találni nyomórugó.
Az elején a mozgató egyenlő a mozgási energia
A potenciális energia a rugó ekkor nulla, mivel a rugó megfeszül.
Ezután a teljes mechanikai energia a rendszer a kezdeti idő:
Abban a pillanatban a maximális kompresszió a tavasz bár a labda megáll, így a kinetikus energia nulla, és a potenciális energia egyenlő az energia a összenyomott rugó. Az összes energia tehát megegyezik
A törvény alapján a természetvédelmi teljes mechanikai energia E2 = E1. kap
Helyettesítő számértékek:
Feladat B5. A tartálytérfogat V = 25,0 literes tartalmaz álló gázkeveréket hélium, amely az anyag mennyiségét v1 = 2.00 mol és az oxigén mennyiségét az anyag, amely v2 = 0,800 mol. Ha az abszolút hőmérséklet a gázkeverék T = 290 K, p értéke a nyomás ezt a keveréket, ... kPa.
Ahhoz, hogy megtalálja a nyomás a gázkeverék a Dalton-törvény. E törvény szerint, a nyomás a gázkeverék az összege a parciális nyomások az egyes komponensek a keverék. Részleges nyomás - ez a nyomás, hogy lenne a gáz, ha a gáz volt csak az edény.
Van két gáz. A parciális nyomása mindegyik találunk segítségével a törvény Mengyelejev-Clapeyron egyenlet:
Találunk a nyomás a keverék:
Feladat B6. Víz térfogata V = 250 cm3 hűti a hőmérséklet t1 = 98 ° C hőmérsékletre t2 = 60 ° C-on Ha a hőmennyiség során felszabaduló hűtővíz teljesen átalakul a munka emelni építőanyagok tömegű m = 1 m, akkor lehet emelni, hogy a maximális h magasság. egyenlő ... dm
A hőmennyiség során felszabaduló hűtővizet formula határozza meg:
A víz tömege lehet meghatározni mennyiségének ismerete és a sűrűség:
Ha az összes energia szabadul fel, amikor a víz lehűl, menj a rakomány emelő, akkor általánosságban elmondható, emelési magasság attól függ, hogy hogyan emelje a terhelést: a gyorsulás, vagy sem, mert ha a terhelés emelkedik gyorsulás, aztán egy részét az energia megy a gyorsulás teher és részben legyőzzük az erőket a gravitáció. Abban az állapotban, arra kérjük, hogy megtalálják a legnagyobb magassága lift. A maximális lehetséges magassága lenne a helyzet, ha az emelő végezzük egyenletesen, azaz a gyorsulás egyenlő nullával.
A szükséges munka, hogy szüntesse meg a m tömegű test h magasságban gyorsítás nélkül egyenlő a különbség a potenciális energia a test:
Mivel az összes elválasztott hőmennyiség az, hogy felemeljük terhelések, akkor Q = A. Ezután
Helyettesítő számértékek:
Feladat B7. A hőmérséklet a fűtőelem egy ideális hőerőgép, hogy At = 100 ° C több, mint a hőmérséklet a hűtőszekrényben. Ha a hűtőszekrény hőmérséklete t = 100 ° C-on A motor hatásfoka termikus hatásfok η egyenlő ...%.
A hatásfok az ideális hőerőgép által meghatározott Carnot:
Feladat B8. A vákuum fénysorompó katód anyaga nikkel (Avyh = 4,5 eV). esik monokromatikus sugárzást. Ha a fotoáram megszűnik egy retardáló feszültség Uz = 7,5 B. az E energiáját beeső fotonok egyenlő ... eV.
Írunk az Einstein-egyenlet a fotoelektromos hatás:
Amennyiben T - a kinetikus energia a kilőtt elektron.
Késleltető feszültség - ez a feszültség, amelynél a fényáram leáll. Amikor egy elektron halad késleltető feszültség, az elektromos mező nem működik rajta:
, ahol e - elektron töltése.
Ez a munka nem fogja megváltoztatni a kinetikus energia az elektron:
Itt figyelembe vesszük, hogy a végső mozgási energiája az elektron nullával egyenlő (megáll).
Vegyük észre, hogy ez a kifejezés és a kilépési munkát az elektron megtakarított energia joule. Átalakítani az energia mennyiségek elektronvoltos kell osztani az elektron töltése e. Ezután az elektron energia elektron-V egyenlő:
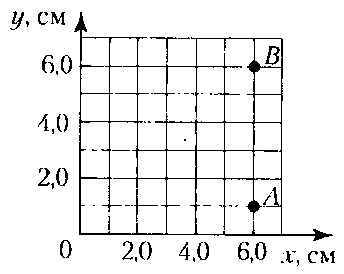
A lehetséges a elektrosztatikus mező által generált ponttöltés egy ponton egy r távolságban a töltés által adott:
Ebben az esetben a két pont közötti távolság A és B:
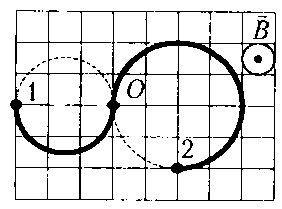
Amikor egy töltött részecske mágneses mezőben hat a részecske Lorentz-erő, amely mindig merőleges a részecske sebessége. Az erő merőleges a sebesség nem változik az arány a legnagyobb, de csak megváltoztatja az irányt a sebességvektor. Ennek eredményeként, a részecske mozog egy kört.
Leírni a mozgás a részecskéket levelet egyenlet Newton második törvénye, tekintettel arra, hogy a körkörös mozgás állandó sebességgel - a mozgás egy centripetális gyorsulás:
, ahol R - a kör sugara.
Az egyenlet Newton második törvénye a részecskék számára:
Vegye figyelembe, hogy ha mozog egy kör mentén állandó sebességgel, a részecskesebesség lehet kifejezni a szögsebesség:
Írunk a kapott reláció a két részecske leírt probléma:
Itt felhasználtuk a tény, hogy a díjak a részecskék azonosak.
Osszuk az első kifejezés a második, ezt kapjuk:
Így a szögsebesség a részecske mozgás egy kör mentén egy mágneses mező fordítottan arányos a részecske tömege. Ez lehetővé teszi számunkra, hogy megtalálja az arány a tömegek.
Az ábra azt mutatja, hogy egy és ugyanazon időben, az ion 1 volt, fél kört, és háromnegyede 2 ion. Ez azt jelenti, hogy a szögsebessége az ion 2 nagyobb, mint a szögsebessége-ion 1, azzal jellemezve,
B11 feladat. Ideális esetben LC kontúr amely egy tekercs induktivitása L = 27 mH és C = a kondenzátor kapacitása 0,50 uF mentes elektromos oszcilláció előforduló. Ha a teljes energia a kontúr W = 54 mJ, az idő, amikor a kondenzátor töltési q = 4,5 SCLC, az I áram a tekercsben egyenlő ... mA.
Az összes energia W áramkör mindig összegével egyenlő energiát az elektrosztatikus mező a kondenzátor és a tekercs mágneses mező.
Ezért tapasztaljuk, hogy a jelenlegi:
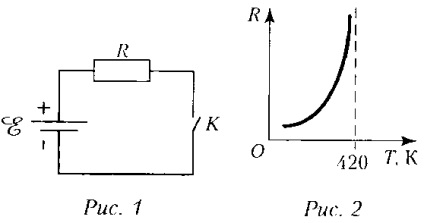
A probléma megoldása érdekében használjuk a törvény az energiamegmaradás.
Hagyja a lánc volt felelős q. EMF forrás közben munkát végző egyenlő
, mivel az EMF - a munka az egységár halad át az áramkört.
A munkát a forrás csak a fűtés ellenállást, mivel az állapot a probléma hőátadás a környezet hiányzik. Ellenállás ugyanazon a hő csak egy bizonyos hőmérséklet 420 K. További melegítés nem lehetséges, mivel az ellenállás válik végtelenül nagy, és a jelenlegi az áramkörben megszűnik.
A fűtőellenállás hőmérséklete T0 T hőmérsékletnek szükséges hőmennyiséget egyenlő
Alkotunk a hő egyensúly egyenlet:
Helyettesítő számértékek: