A fogyasztói döntés optimalizálás 1
A fogyasztó, miután a jövedelem akar tölteni, és természetesen, a legnagyobb hasznot. Előny értetődő szempontjából a preferenciális rendszer vagy a hasznosság függvény. Tanulmányunkban néztük meg, hogyan lehet optimalizálni a fogyasztók választási lehetőségeit.
1. A feladat optimalizálása a fogyasztók választási lehetőségeit
A lényege optimalizálása a fogyasztók választási lehetőségeit.
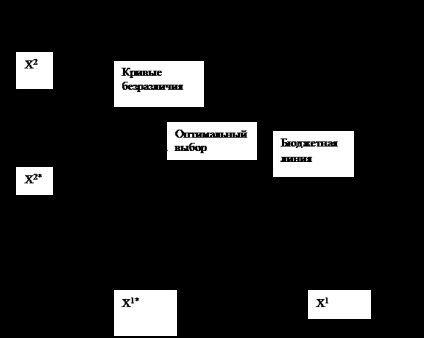
Kiválasztása (X 1 *. * 2 X) a legjobb választás a fogyasztó számára. A halmazát, amelyek legszívesebben (X 1 *. * 2 X), azaz egy halmazát, ez felett található a közömbösségi görbe nem metszi a készlet, hogy engedheti meg magának vásárolni, és ez határozza meg a költségvetési tételt. Így, egy sor (X 1 *, X 2 *) - ez a legjobb készlet, amely a fogyasztó engedheti meg magának.
Annak érdekében, hogy ezt a problémát kell használni mellékleteként találni korlátozott optimalizálási felhasználásával Lagrange szorzók.
Mivel az egyéni fogyasztók választhatnak, hogy mennyi minden általuk vásárolt termék, figyelembe véve a preferenciák és a költségvetési megszorítások? Azt feltételezzük, hogy a fogyasztók, hogy ez a választás racionális okokból - úgy döntenek, áruk maximalizálása elégedettség alapján vezetjük a korlátozott költségvetés rájuk.
Megfelel a piaci kosár két feltételt kell teljesítenie:
1. Meg kell elhelyezkedik költségvetési tétel. Miért? Figyeljük meg, hogy minden piaci kosár a bal oldalon, és az alábbi költségvetési tétel hagy némi fel nem használt részét a jövedelem, amely, ha kiégett, növelheti az ügyfelek elégedettségét. Természetesen, a fogyasztók - és néha nem teszi meg -, hogy mentse egy részét a jövedelem jövőbeni fogyasztást. Azonban, ahogy helyzetének megkönnyítése, azt feltételezve, hogy minden jövedelmet töltött azonnal. Szintén fontos megjegyezni, hogy a piaci kosár a jobb és magasabb a költségvetési sor nem vásárolható meg ezen a szinten a bevétel. Ezért az egyetlen ésszerű és megvalósítható választás - egy kosár feküdt a költségvetési tétel.
2. Meg kell, hogy a fogyasztó a legelőnyösebb kombináció az áruk és szolgáltatások.
E két feltétel csökkenti a maximális elégedettség a fogyasztói kérdés, hogy az a kérdés, kiválasztja a megfelelő pont a költségvetési tétel.
Ha elemezzük a problémát grafikusan a fogyasztói választás az élelmiszer és a ruházati cikkek, arra lehet következtetni, hogy a kosár, amely összehozza a maximális elégedettség, kell alapulnia a legmagasabb közömbösségi görbe vonatkozó költségvetési tétel. Abban az érintési pont a költségvetési tétel és a közöny görbe meredeksége költségvetési tétel pontosan megegyezik a lejtő egy görbe közöny. Mivel a határ helyettesítési rátáját (MRS) egy negatív érték, a fordított tilt közömbösségi görbe, azt lehet mondani, hogy a megfelelés éri el a maximumot (adott költségvetési korlát) azon a ponton, ahol a
A feladat választás optimalizálását a fogyasztó lehet tekinteni, mint egy alkalmazás a módszert kell találni a feltételes szélsőérték a Lagrange szorzók.
Feltesszük, hogy minden tétel ára pi, és az egyén jövedelme Q - egy bizonyos összeget, amelyben jár, vesz neki egy sor kívánt termékeket. A vásárlás egy sor áru X = (xi, ..., xn) szükséges pénzt költeni az összeget a C (x) = pi xi + ... + pn xn =
Így az egyén csak vásárolni egy sor X, ahol PX≤Q. Ezért, egy több sorozat termékek, a számára rendelkezésre álló Q. jövedelem B = B (P, Q) =. Ez a készlet az úgynevezett költségvetési sor. Olcsó készlet zárt és korlátos.
Bizonyítás. Legyen r = min pi. Aztán, ahogy az jól látható, ha X
B, majd x≤Q / r i = 1, ..., n, azaz a set B korlátozott. Lássuk be az elszigeteltségből. Let Xk
Mint minden k
Z. Aztán a folyamatos lineáris függvény
PZ és mivel PXk ≤Q, majd PZ≤Q. Következésképpen, Z
A határ a költségvetési halmaz halmaza G =
B: PX = Q>. A határ G - egy szegmens esetében a két termék, egy része a sík által határolt háromszögben, abban az esetben a három termék, és általában van egy része a hipers'ık a térben az áruk.
Megfizethető set B (P, Q) függ a jövedelmek Q és P árrendszer, de minden egyes jellemzőit, mint például az általa előnyben részesített rendszer független.
A fogyasztó, miután a jövedelem akar tölteni, és természetesen, a legnagyobb hasznot. Előny értetődő szempontjából a preferenciális rendszer vagy a hasznosság függvény. Ez vezet a következő probléma matematikai programozás.
Keressen egy sor áru X = (xi, ..., xn), maximalizálva a hasznossági függvény u (xi, ..., xn), amikor a költségvetési korlát PX = pi xi + ... + pn xn ≤Q; értelmében a feladat minden változót nem negatív értéket, vagyis a xi ≥0, i = 1, ..., N.
Úgy véljük, a problémát meg lehet megfogalmazni tömören:
Mivel u (X) - folytonos függvénye érveit, és a költségvetés meghatározott korlátozott és kompakt, akkor u (X) eléri a beállított a maximális, azaz 1. probléma van egy megoldás. Nyilvánvaló, hogy bármely ponton X * maximum funkció c (X) fekszik a határán G költségvetési sor. Sőt, ha azt feltételezzük, ellenkezőleg, vagyis azt, hogy a Z - a maximális pontot, de a Z
G, majd a PZ
B, de u (Z + Y)> u (Z). Annak a ténynek köszönhetően, hogy minden terméket kívánunk. Ez ellentmond az a tény, hogy a Z - maximális pont a függvény c (X) állítsa be a költségvetésbe.
Feltétel: Ha u (X) - szigorúan konkáv, akkor a megoldás az (1) lehetséges, azaz Csak egy pont a maximális hasznosság függvény a költségvetési sor.
Emlékezzünk, hogy a funkció u (X) nevezzük szigorúan konkáv, ha bármely X, Y az a tény, hogy a 0 <λ<1 следует, что u(λx+(1-λ)Y)> # 955; u u (X) + (1- # 955;) u (Y).
Bizonyítás. Tegyük fel, hogy az A és a C - két csúcs pontot, azaz, u (X)
u (A) = u (C) bármely pontjára X B. Már tudjuk, hogy a A és C pontok hazugság határán a megadott költségkeretet, azaz RA = RS = Q. Tekintsük a ponton E = A / 2 + C / 2. Látjuk, hogy PE = P (A / 2 + C / 2) = Q, azaz E
B. Tekintettel a szigorú konkáv u (X), van: u (E)> u (A) = u (C). Ez ellentmond az a tény, hogy az A és C - vannak olyan pontok maximális a költségvetésben beállított.
Így, amikor a szigorú konkáv hasznossági függvény létezik a költségvetésből egy ponton maximális hasznossági függvény. Így a fogyasztó nem is kell a döntést, hogyan költsék a pénzüket a legtöbbet, mert van egy egyedülálló termék, a hasznosság maximalizálása. Ez az egyetlen csúcspontja az úgynevezett pont a kereslet, vagy egyszerűen csak egy fogyasztói kereslet. Ez a pont jelöli X *.
Tanulmányozzuk a lényeg a kereslet. Bár létrehozott csak azt, hogy feküdjön a határ a költségvetési halmaz. Így a probléma (1) csökkenti a következő:
Ezt a problémát meg lehet oldani a Lagrange szorzók. A Lagrange-függvény L (X, # 955;) = u (X) + # 955; (Q-PX), megtaláljuk a részleges származékok és azokat azonosítani nullával:
Így csak egy pont a maximális hasznosság függvény a költségvetési sor.
Ezért a fogyasztó nem is kell a döntést, hogyan költsék a pénzüket a legelőnyösebb, mivel van egy egyedülálló termék, a hasznosság maximalizálása. Ez az egyetlen csúcspontja az úgynevezett pont a kereslet, vagy egyszerűen csak egy fogyasztói kereslet.