Függvény deriváltját. Differenciálás. Egy algoritmust kiszámítására származék
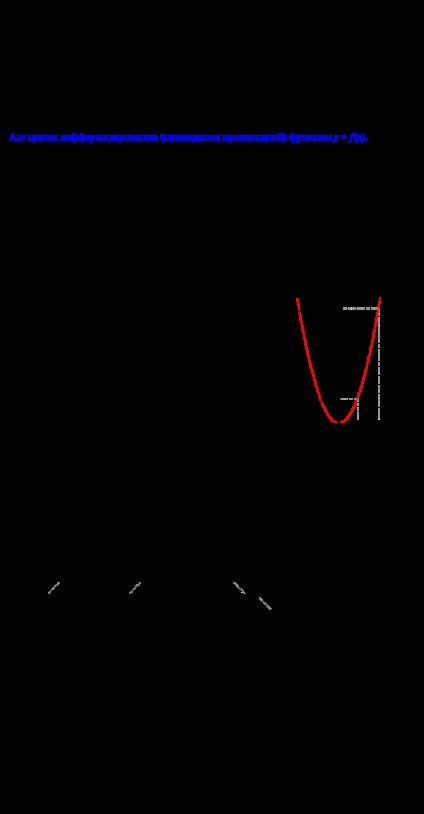
Ahhoz, hogy megértsük származék, egy függvényt definiálunk y = f (x). Hagyja, hogy a grafikon ennek a funkciónak a görbe (lásd az ábrát).
1) az x tengelynek egy tetszőleges pont XO veszi. Az Y tengely az egy pont s f (Ho). A metszéspontját két koordináta, hívja A.
2) Adunk egy pont XO növekmény Ax és kaphat egy új pont az abszcisszán: Ho + Ax. Mi elvégezzük ugyanezt az eljárást: így egy második pont a görbén a B, és vegye figyelembe a megfelelő pontot a y-tengely: F (Ho + Ax). A különbség a két pont az y-tengely - ez a növekedés Au funkciót. Azaz:
3) Rajzolj egy szelő a A és B pontok
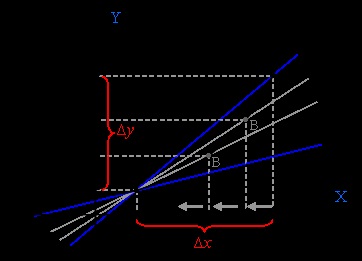
4) Mi legyen a növekmény Ah nullára - azaz, hogy pont Ho. Akkor a keresztirányú elkezd forogni, és a B pont folyamatosan közeledik egy görbe pont A. A növekmény Δy funkciót is nullához és keresztirányú eléri a határértéket helyzetbe, amikor a grafikon görbe vele lenne az egyetlen közös pont A. A vágás ez lesz a érintőleges függvény grafikonját a ponton xo. Ez azt jelenti, azon a ponton, XO egyedi határérték között Δy és Ah eléréséig. Így Δy Ah, és nem nulla, de végtelenül mennyiségben. Ha az X tengelyen vett az időskálán t, a Ah ponton xo azonnal közel nulla. Ha az Y tengely vesszük a skála a távolság S, akkor a f pont (Ho), megkapjuk a távolságot, amelyet a test átment időpontban XO. A elosztjuk Δy szóló Ah Ho. megkapjuk semmi, de a pillanatnyi átlagos időpontban xo (V = S. t). Tehát egyszerre határozza meg a fizikai értelmében ez a jelenség. A matematikában, hogy van egy másik neve: ez egy származéka. Úgy hívják a változás mértéke a függvény egy adott pontban.
Kapcsolódó cikkek