Henry Dudeney - 200 híres rejtvényeket a világ - 29. oldal

Azt az ábrán látható, amint lehet elhelyezni egy sakktábla 12 lovak (a lehető legkisebb számú), úgy, hogy amikor minden egyes cellában vagy elfoglalt, vagy fenyegeti a ló támadást. Menj végig a sejtek a sorba, és azt találjuk, hogy ez a helyzet ezen a módon. Határozzuk meg most a legkisebb számú ló, amely előírja, hogy minden sejt volt, vagy foglalt, vagy támadás alatt, és minden ló védi egy lovat. Hogyan gondoskodik ezek a lovak? Meg kell jegyezni, hogy a 12 ábrán látható mindössze 4 lovak védett ezen a módon.
biztonságos sakktábla
Egy hagyományos sakktábla 8 × 8 minden cella lehet védeni (azaz, akár üres, vagy megtámadta) öt királynők - a lehető legkisebb mértékben. Vannak pontosan 91 alapvetően eltérő elrendezés, amelyben sem a királyné nem támadja egy dáma. Ha minden királynő meg kell támadni egy dáma (vagy őket védeni), akkor van legalább 41 helyen, és úgy találtam, 150 amelyek szerint bizonyos királynők megtámadta, és vannak, akik nem, de az utóbbi esetben nagyon nehéz pontosan felsorolni az összes megoldásokat.
Egy hagyományos védheti nyolc varjak (a legkisebb szám) 40 320 módon sakktábla minden sejt, ha sem hajó nincs joga megtámadni egy másik hajót, de nem ismert, hogy sokan alapvetően különböző módon (lásd. Fent a probléma megoldására „Nyolc varjak”) . Nem számít, hogy milyen módon minden egyes hajó védi a másik bástya.
Egy hagyományos sakktábla minden cella védhető nyolc elefántok (a legkisebb szám), ha van ilyen Bishop nem engedélyezett megtámadni egy másik elefánt. Ha minden püspök védeni kell, akkor kell 10 elefántok (lásd. Fent a puzzle „Védtelen elefántok” és a „védett elefántok”).
Egy hagyományos sakktábla minden cella védhetők tizenkét ló, ha az összes lovat, hanem négy nem védett. De ha minden ló meg kell védeni, hogy úgy 14 lóval (lásd. Fent teaser „védelme a lovakat”).
Ha az üzlet a királynők n × n-táblák, ahol n kevesebb, mint 8, akkor az érdeklődés a következő eredménnyel:
1 queen megvédi az alaplapot 2 × 2 egyik jelentős módon;
1 queen védi tábla 3 × 3, az egyik jelentős módon;
2 queen védelme fedélzetén 4 × 4 három szignifikáns módon (védő egymással);
3 queen védelme fedélzetén 4 × 4 két fontos szempontból (nem védik egymást);
3 queen védelme fedélzeten 5 × 5 harminchét szignifikáns módon (védő egymással);
3 queen védelme fedélzeten 5 × 5 két lényeges módon (nem védik egymást);
3 queen védelme fedélzeten 6 × 6, egy szignifikáns módon (védő egymással);
4 queen védő fedélzeten 6 × 6 tizenhét szignifikáns módon (nem védik egymást);
4 queen védelme fedélzeten 7 × 7 öt szignifikáns módon (védő egymással);
4 queen védelme fedélzeten 7 × 7 egy szignifikáns módon (nem védik egymást).
Található a sakktábla, nem fenyegeti támadás
Tudjuk, hogy a királynők mindig hely egy négyzet tábla n 2 sejteket (ha n> 3), úgy, hogy nincs királynő nem támadja meg egy dáma. Ugyanakkor az általános képlet a számot, hogy megtalálják az összes ilyen elhelyezések, amelyek még nem találtak; Valószínűleg, egyszerűen nem létezik. Ismert eredmények:
ha n = 4, van egy alapvető megoldás, de csak 10 döntéseket;
ha n = 5, két alapvető megoldás, és megoldások csak 10;
ha n = 1 6 létezik egy alapvető megoldás, és megoldások a 4;
ha n = 7, van 6 lúgos oldatok, és összesen 40 oldatok;
ha n = 8 van 12 lúgos oldatok, és oldatok 92;
ha n = 9, 46 léteznek alapvető megoldások;
ha n = 10, vannak 92 lúgos oldatok;
n = 11 van 341 alapvető megoldás.
Nyilvánvaló, n varjak lehet helyezni a táblán n × n úgy, hogy azok nem támadják egymást, n! módon, de hányan alapvetően különbözik voltam képes megtalálni csak négy olyan esetben, amikor n = 2, 3, 4 és 5 válasz lesz, illetve 1, 2, 7 és 23 (ld. puzzle „Négy Lions”).
Tudunk szállást 2n-2 elefántok a fedélzeten n × n két módon (lásd. Logikai „Collection elefántok”). A táblák oldalsó 2, 3, 4, 5, 6, 7, illetve 8, vannak olyan sejtek, 1, 2, 3, 6, 10, 20, 36 alapvetően különböző intézkedések. Abban az esetben, a páratlan n, van 2 1/2 (n-1) az ilyen kiosztások, amelyek mindegyike generál útján forgatás és reflexiók más elhelyezési 4 és 2 n-3 -21/2 (n-3) elhelyezését, generál 8 más helyeken. Abban az esetben, a páros N, van 2 1/2 (n-2). minden keresztül forgatás és a reflexiók generál 4 és 2 n-3 -2 1/2 (n-4). generáló 8 helyezések.
A fedélzeten, és x és tudunk szállást ½ (n 2 + 1) a lovak, nem támadja egymást, ha n páratlan egyik jelentős módon, és amikor még, majd ½n 2 ló is lehetséges befogadni az egy jelentős módon. Az első esetben, mindannyian lovak elhelyezése a sejtek ugyanolyan színű, mint a központ, és a második esetben, mi mindet egyszerre csak fekete vagy csak fehérvérsejteket.
Problémák a két alakkal
A fedélzeten n 2-sejtekben található két queen, két bástya, két püspök, két vagy ló mindig lehet elhelyezni (tekintet nélkül arra, hogy azok támadni egymást, vagy sem) módszerek. A következő képletek mutatják, hogy hány módja a két szám lehet elhelyezni a feltétellel kölcsönös támadás és nélküle.
(Lásd. Logikai „Vadászat egy oroszlán.”)
Dinamikus sakk problémák
147. A túra csónak. Csak meg kell mozgatni a hajót az egész fórumon, hogy meglátogatta minden sejt pontosan egyszer, és befejezte a túra a sejtet, ami elkezdődött. Tehát szükség van, hogy ezt a lehető legkevesebb mozog, de ha nem nagyon óvatos, majd egy éles fordulatot, hogy egy több, mint amire szüksége van. Természetesen a cellát kell tekinteni „látogatott” abban az esetben, ha csak menjen át rajta, és abban az esetben leállítás. Mi azonban nem kell aggódni álokoskodás mint az a tény, hogy meglátogatjuk kétszer az eredeti négyzet. Feltesszük, hogy látogassa meg egyszer.

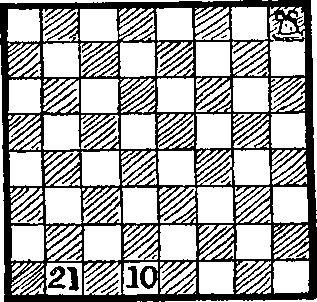
148. A hajókiránduláson. A címe ez a puzzle nem véletlenül használja a „utazás”, mert a „utazás”: a visszatérés az eredeti helyére, és ebben az esetben nem fogjuk ezt csinálni. Bástya teszi 21 Természetesen látogató minden téren a tábla pontosan egyszer, leállítja a 10 cella végén a tizedik stroke és végül utazik a cellában 21. Két egymást követő agyvérzés nem lehet tenni ebben az irányban; Más szóval, meg kell forgatni minden lépés után.
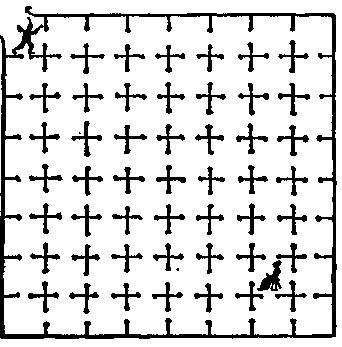
149. Egy másik vágyakozó lányba. A gonosz báró a régi szép napok egyik bebörtönzött egy ártatlan hajadont mély börtön volt, ami alatt az árokban a vár. Itt látható az alvilági 63 kamra, amelyet összekapcsolt nyitott ajtó, és egy kamra, ahol a szűz láncolt. A vitéz lovag, aki szerette a leányt, képes volt megmenteni a kezében az ellenség. Miután elérte a bejáratnál a labirintusból, mint az ábrán látható, akkor majd el, és a kamra, ahol a szűz pined látogató útközben mindegyik kamra pontosan egyszer. Vegyünk egy ceruzát, és megpróbálják azonosítani az útjába kerül. Miután ez sikerült, próbáljuk ily módon a 22 egyenes szakaszok. Ezt meg lehet tenni, még ne keresse fel a kamera kétszer.
150. Dungeon. Történt egyszer Franciaországban, hogy az egyik fogoly a saját bűneiért, vagy a bűneit, hogy a külföldi dobták egy börtön, ahol nem voltak 64 kamrák összekapcsolt nyitott ajtók, ahogy. Rendelni valamit, hogy felcsillan a monotónia bebörtönzése, ő találni egy másik puzzle. Itt az egyik közülük.