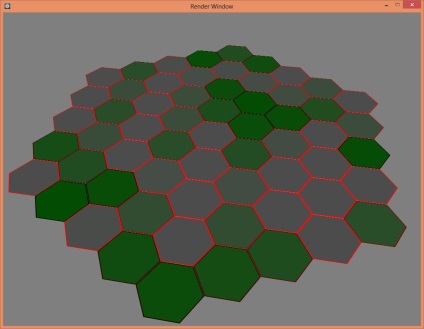
Egyszerű generációs hexagonális (hatszögletű) mesh mátrix forgási középpontjához bármilyen szögben

Jó napot kívánok. Nemrég belefutottam egy problémát generáló hexagonális rács található. Vannak módszerek vonalai. Ezek alkalmasak, amit akarsz. És ez a módszer találtam. Talán rossz látszó, ki tudja. A fórum, én felajánlott három görbe megoldások:
1. Crutches (olyan opció, ami a legrosszabb).
2. Generation sor és öntsük a szükségtelen. Elvileg a helyes döntés, de sajnos, azt kell, hogy a központtól. Ezután kényelmesen hozzá a kívánt sejtek lesz.
3. A ferde koordinátákat. Ez egy komplex megazhest, amely képes megölni egy felhő idő. Azt még nem sikerült elsajátítani.
És most térjünk vissza a mi algoritmus.

A lényeg az ujjak

Meg kell, hogy a cellás szerkezet ala ezt.

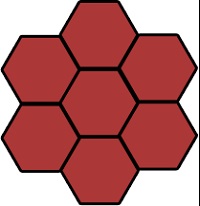
Az első lépés a generációs az első, a központi hatszög.

Ha a közönség egészen tisztánlátó, észrevette, hogy a szomszédos oldala a sejt képez a mátrix tengely.

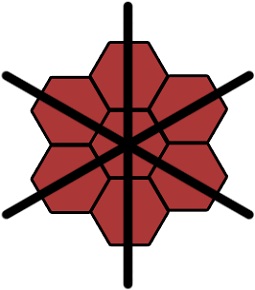
Az első sorban nincs gond, ha tudod, hogy a sugár és szög, akkor az összes hatszög alkotnak, ahogy kellene. Problémák jön a második sorban. Egyes sejtek nem hazudnak, ha ez szükséges. És az ok a következő. A mi szerkezete van időközönként. De ez nem kör alakú, és hatszög. Csak az első sorban közelítenek egymáshoz.

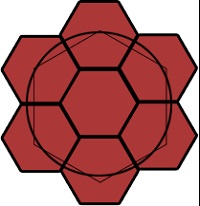
Az ábra azt mutatja, hogy a központok a hatszög és feküdt a kör, és egy hatszög mátrixban. Azonban a második sorban a probléma jól látható.

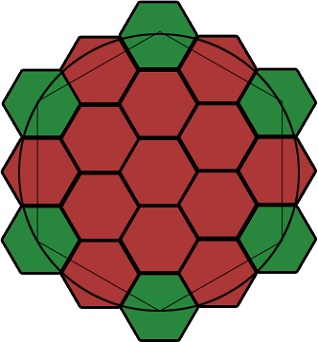
Úgy látszik, hogy csak a tengelyirányú hatszög (zöld) egy körön. A fennmaradó központok felé tolódott a központ és fekszenek a hatszög mátrixban. Ezért, a sugaras szimmetriája egy rács nincs beállítva.
Ez magában foglalja a következő határozatot.
Építs egy első tengelyirányú hatszög.
Ezután kiszámítjuk a vektorok. Az ábra azt mutatja, az irányt a vektorok. Meg lehet fordítani.

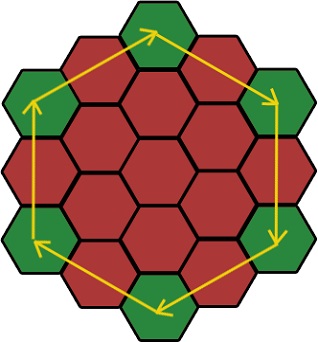
De nem kell ezt vektor. Vagy inkább ő maga nem, de egy részét.

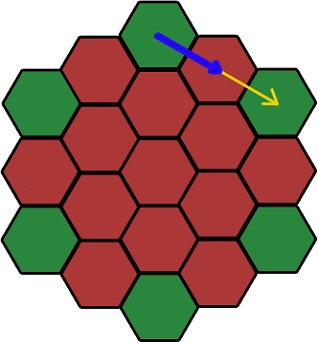
Szükségünk van a kék vektor. Ez offset hozzá, hogy az axiális hatszög megszerzésének pontos koordinátákat. Sárga vektor osztva az alkatrészek száma egyenlő a számát hatszögek közötti axiális hatszögek + 1 (vagy a réteg szám).
Ezt követően, akkor létrehoz egy tetszőlegesen nagy tömb közepén.

És most a kód a felháborodást. Én programozott Xors3D, de azt hiszem, hogy bárki is, meg fogja érteni, hogy ez a dolog működik (annál is inkább, az egyszerű kódot, és okait lásd fentebb). Elég csak az egyik funkció - a funkció létrehozása egy cellába.
Itt a kód.

Vector kiszámítása
Ha megrendelése> 0 Then - kiszámítani a vektor, amikor egy szám nem nulla (ahol a központi hexa)
Vektor (i, 0) = ((CellRadius * sin (szög + 60) * rendelés-CellRadius * sin (Szög) * rendelés)) / (rendelés) - 0 = X, az első vektor koordináta
Vektor (i, 1) = ((CellRadius * Cos (szög + 60) * rendelés-CellRadius * Cos (Szög) * rendelés)) / (rendelés) - 1 = Z, a második koordináta vektor
End If
következő

Mi van a kimeneten:

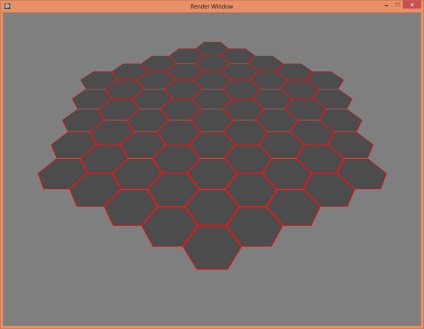
Frissítése 1.0 - forgás bármely szögben mátrix

Előfordulhatnak olyan helyzetek, amikor a hexagonális rács kell lennie valahol, hogy csatlakozzon derékszögben. Gondolkodtam rajta, és modernizálják a funkció - akkor most forgatni a teljes tömböt bármilyen szögben!
Tehát a kód:

Fontos különbség:
Funkció CreateCell (X #, Z #, rendelés%, AddAngle%) - van egy új érv, ez egy tetszőleges szöget - AddAngle.
Szög # = 360 / Limit * i + AddAngle - hozzáad egy ofszet kiszámításához a szögek és vektorok.
xRotateEntity Cell \ Sprite, 90, -AddAngle, 0 - Sprite forgása egy függőleges tengely körül az ellenkező irányba.

Mi van a kimeneten:
17 fok.

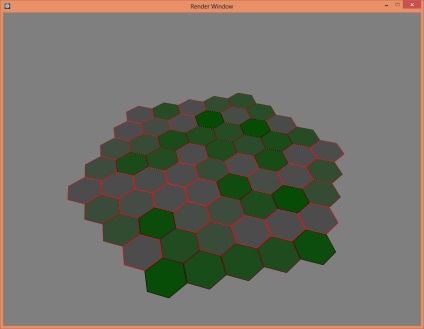
30 fok.

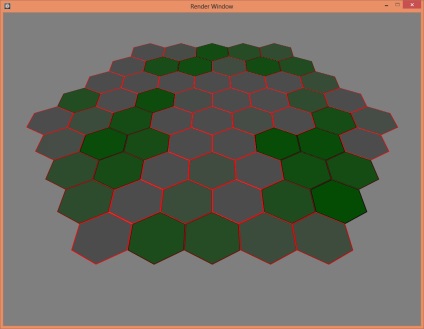
10 fok.