fizika
Virtuális laboratóriumi munka № 8
"A FRIKCIÓK EGYSZERŰSÉGE MEGHATÁROZÁSA"
A munka elméleti alapjai.
A munka fő célja, hogy meghatározza a súrlódási együtthatót a kocsi és a sínek kereke között. Feltételezzük, hogy a kerekek csúszás nélkül forognak, amikor a kocsi elmozdul. Ebben az esetben a súrlódási tényező a gördülés súrlódási együtthatója. Ennek az értéknek a kiszámításához az alap alapja a fizika alapvető törvénye: a lendület megőrzésének törvénye és az egyik típusú energiának a másikba való átmenetéhez kapcsolódó szabályszerűségek. Tekintsük át ezen szabályszerűségek alkalmazását egy ágyúgolyó és egy terhelésű kocsi ütközésének bemutatott modelljéhez. A lövés után az ágyúgolyó és a kocsi zárt rendszernek tekinthető, amelynek teljes lendülete állandónak és nulla értéknek kell lennie. Mivel a mag beragad az autóba való belépés után, azt feltételezzük, hogy ezeknek a testeknek a kölcsönhatása teljesen rugalmatlan. Tegyük fel, hogy a jelen esetben a lendület megőrzésének törvényét skaláris formában írjuk:
ahol M a terheléshez tartozó kocsi tömege, m az ágyúgolyó tömege, v a sejtmag repülésének sebessége, u pedig a test mozgásának teljes sebessége a kölcsönhatás után. Az (1) egyenlet bal oldala a rendszer lendülete a kölcsönhatás előtt, amely csak a mozgó mag lendületéből áll, mivel a kocsi álló helyzetben van. Az egyenlet jobb oldala a rendszer impulzusa az interakció után - a mag és a kocsi, amelyek ugyanolyan sebességgel mozognak:
Most gondosan fontold meg az energia kapcsolatokat. Ha a rugalmatlan kölcsönhatás után a testek sebessége nem nulla, ezért ez a rendszer rendelkezik az Ekc kinetikus energiával. amely meghatározható:
Mielőtt az ütközési kinetikus energia csak egy maggal rendelkezett, és ez az energia Ek = egyenlő
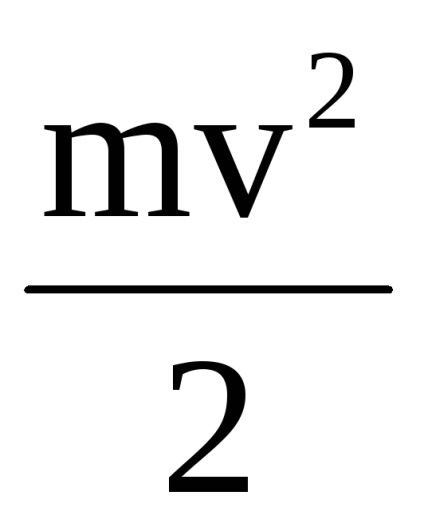
kifejezés
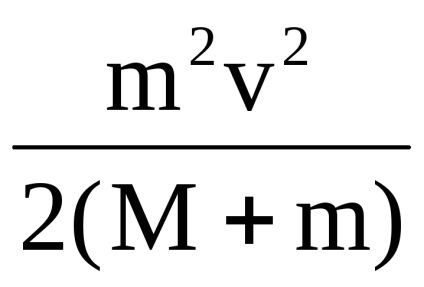
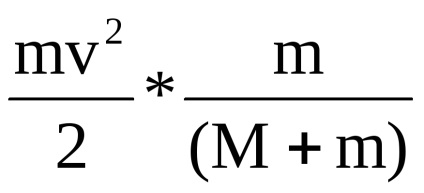
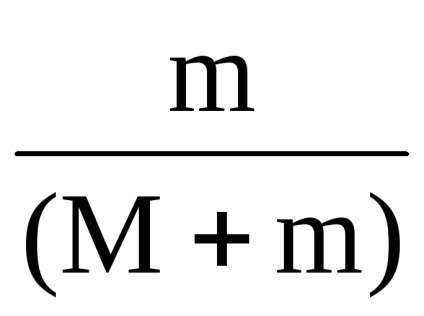
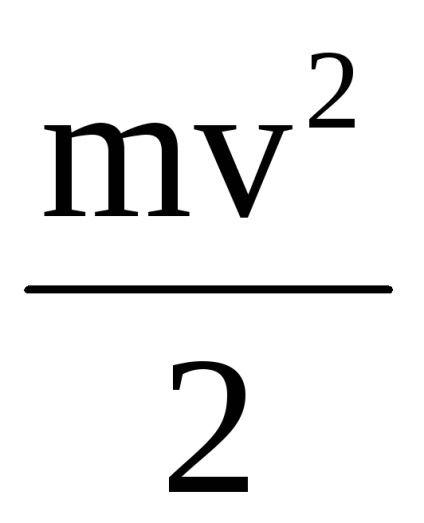
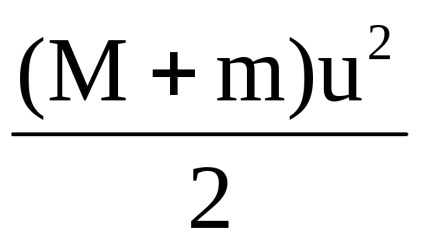
ahol Q a testek melegítéséhez és deformációjához átvitt energia. Tehát a mag teljes mechanikai energiája nem maradt nyom nélkül, de átjutott a testrendszer rendszerének kinetikus energiájába és ugyanazon rendszer belső energiájába.
Miután a mag megütötte a kocsit, a testrendszer elkezdett mozogni, de most a vizsgált rendszer nincs lezárva, mivel nem konzervatív súrlódási erők járnak el, aminek következtében a kocsi megáll. Az ilyen erők hatása teljesen megegyezik a külső erők rendszerének hatásával. Hol fog mozogni a testek Ekc rendszerének kinetikus energiája? A kérdésre adott válasz abban a felismerésben rejlik, hogy ha a rendszer nincs lezárva, a teljes mechanikai energia csökkenni fog, és a mechanika megváltozását jellemzõ mennyiség mûködik. Most azt mondhatjuk, hogy a bezárt magtoló rendszer kinetikus energiája megváltozott az értéktől
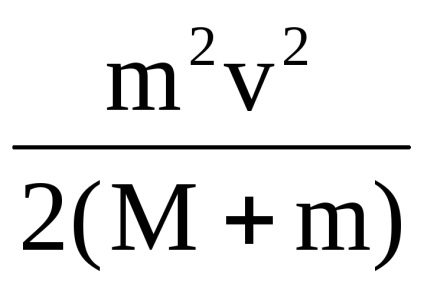
Ebben az esetben a súrlódás ereje a kocsi teljes mozgási pályája mentén állandó lesz. A súrlódási erők munkájának végeredménye ismét a dörzsölő felületekkel érintkező testek belső energia növekedésének tekinthető. A példában szereplő mechanikai munkát a következőképpen ábrázolhatjuk:
S a kocsi kereszteződésének útvonala, ahol Ft = kN, ahol k a súrlódási együttható, N a sínen lévő normál kocsi nyomásának ereje. Vízszintes mozgással ez az erő megegyezik a gravitációs erővel: N = (M + m) g. Most (6) képviseljük az összes u (7) mennyiséget:
Végül a súrlódási együtthatóhoz jutunk:
A telepítés számítógépes modelljének leírása.
A program letöltése után egy régi ágyú, egy kocsi és vezérlőgomb jelenik meg a monitor képernyőjén. A kocsi a síneken áll, amellyel a távolságméret össze van kapcsolva, és amelyen a kernel ütközése után meghatározható a kocsi visszaszerelése. Információ a súlya a mag, és a mag kocsi repülési sebesség felső vonalak a képernyőn, meg kell jegyezni, hogy az egyes programok kezdeni ezeket a tömegeket változhat, és minden égetés a lövedék sebessége eltér a fegyver csöve megváltozik. A súrlódási együtthatót a számítógép egyaránt random változóként határozza meg, így minden munkát végző hallgató esetében ez különbözhet. Trolley megadása után a nucleus mozog egy bizonyos távolságot, amely meghatározza a tömeg, és az arány az indulás kernel súrlódási együttható. Minden lövésnél ez a sebesség is más lesz. A kocsi visszahúzási távolságának méréséhez használja a hozzá csatolt mutatót, amelyet a kocsi elején egy nyíllal fog látni. Az ár egy kisméretű olyan távolságban 0,1 m. Figyelembe véve a helyzet a kocsi, hogy a lövés lövés után, akkor képes lesz arra, hogy meghatározza, hogy milyen távolságban újból a kocsi a rakomány és a kernel a lövés után. A gombokon található üzenetek nem igényelnek külön magyarázatot, és minden felhasználó számára érthetőek. Ha egy lövés után a kocsi elindul a képernyőn, akkor ezt a kísérletet nem szabad figyelembe venni.
Keresse meg a "Work No. 8" ikont a monitor képernyőjén, és kattintson rá kétszer egymás után. A monitor képernyőjén egy kísérleti modell lesz, amely természetesen viszonylag nehéz megvalósítani. A mérési táblázatban rögzítsük a mag tömegének és a targoncának a terhelés értékét. Ezek az értékek nem változnak a kísérlet során, ha nem indítja újra a programot. Most indítsd el a kísérletet.
1. Írja le a mérési táblázatban a magnak a pisztolyhüvelyből való kilépésének sebességét az első esetben. A vázlatban vegye figyelembe a távolsági skála nézõpontjának pozíciójának tervezetét, és ezt az értéket feltételes nulla értékként vegye figyelembe.
2. Nyomja meg a start gombot. Lesz egy lövés, és a kocsi egy kicsit visszafordul. Jelölje meg ezt a pozíciót és határozza meg a kocsi visszahúzásának távolságát. Jegyezze fel a visszavezetés összegét a mérési táblázatban az adott mag indulási sebességének megfelelő gráfban. Helyezze vissza a kocsit az eredeti helyére.
3. Fusson 5-6 lövés, minden alkalommal, amikor rögzíti a kocsi visszahajtásának sebességét és távolságát. Jegyezze fel a méréseket a tanárból. Most a laboratóriumban vagy otthon, folytassa a számításokat.
4. A (9) képlet segítségével számolja ki az egyes lövések súrlódási együtthatóját az eredményeket a táblázat megfelelő oszlopában.
5. Az abszolút hiba kiszámításához használja a közvetlen többszörös mérési algoritmust.
6. Kerülje el a hibát és az eredményt az előírt formában történő írásával.